Paper Reading: TurboIso, Construction

2025년 저는 데이터베이스 랩에 컨택하여 학부 졸업 연구 주제를 받아서 진행하고 있습니다. 저의 주제는 “Continuous Subgraph Matching”과 관련해 코드를 최적화 하고 개선하는 것으로 그래프 쿼리 관련 논문을 읽고, C++ 코드를 튜닝하고 있습니다. 졸업 마지막 학기에 듣는 수업인데 많은 노하우와 경험을 쌓고 졸업하기를 기대하고 있습니다 ㅎㅎ

Wook-Shin Han, Jinsoo Lee, and Jeong-Hoon Lee. 2013. TurboISO: Towards UltraFast and Robust Subgraph Isomorphism Search in Large Graph Databases

들어가며

SymBi(2021) 논문([1], [2], [3])에 이어 이 논문도 지금 졸업 연구를 하고 있는 연구실에서 작성한 논문 입니다! 졸업 연구를 하면서 이 논문의 구현도 살펴볼 일이 있어서 논문 리딩을 진행하게 되었습니다!

Matching Order is Important

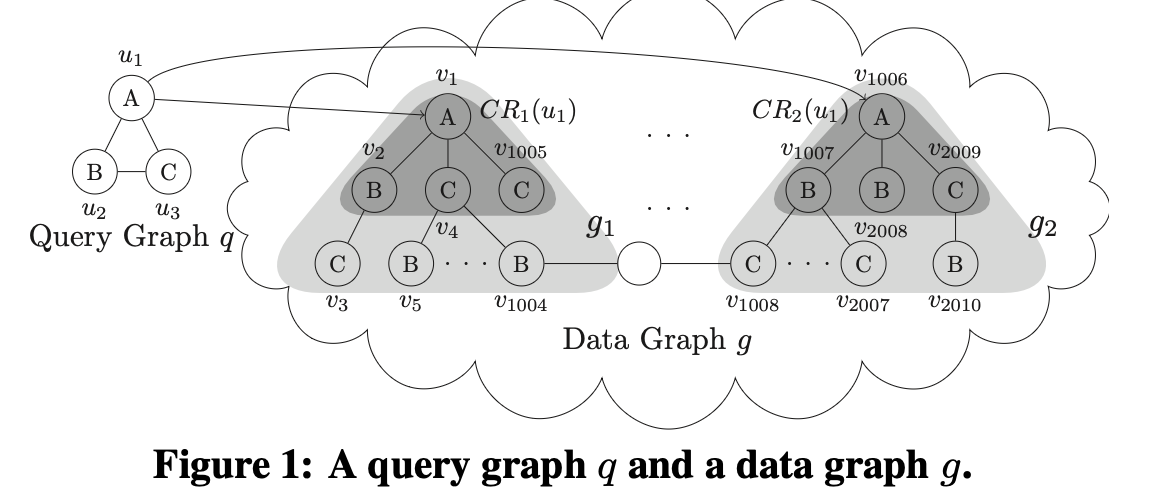
논문에서 제시한 예시 쿼리&데이터 그래프 입니다. 데이터 그래프는 $g_1$와 $g_2$의 서브 그래프로 구성 되어 있습니다.

참고로 Fig1 그림에서는 쿼리 그래프와 매칭되는 패턴이 존재하지 않습니다! 그러나, 매칭이 없다는 것을 빠르게 확인하는 것도 중요한 문제 입니다.

Try to match $g_1$

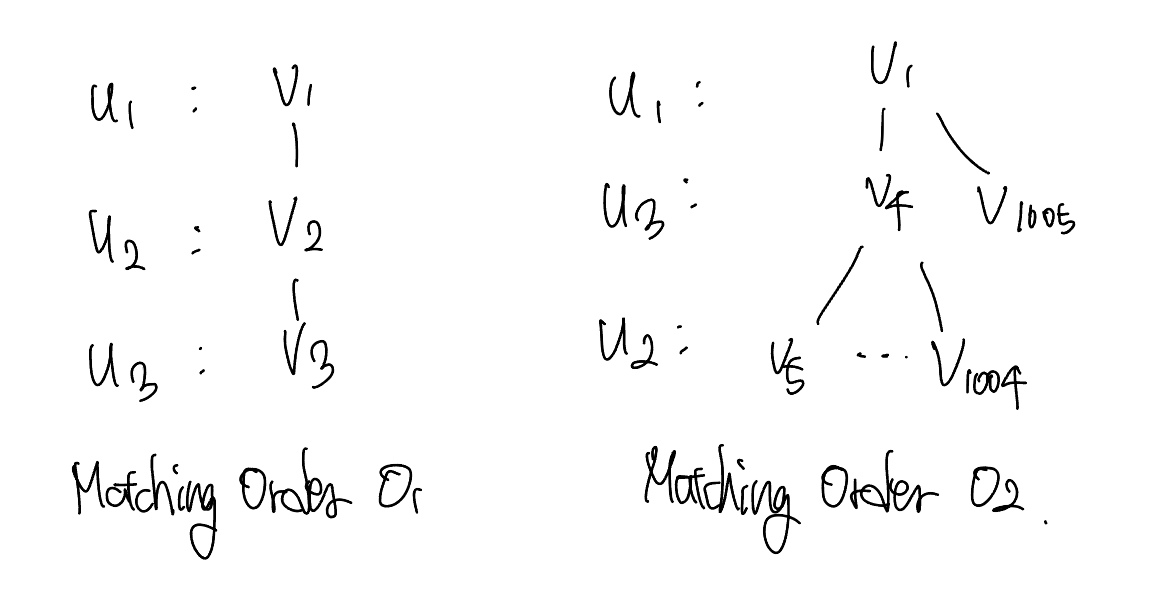
쿼리 그래프를 $O_1 = (u_1, u_2, u_3) \sim (A, B, C)$의 Matching Order 순서로 서브 그래프 $g_1$에 매칭 시켜 봅시다. 그러면, 매칭이 왼쪽 그림의 순서로 맺어집니다. 그런데, 이것은 쿼리 그래프에 대한 임베딩이 아닙니다! $(u_1, u_3)$는 연결 되어 있지만, $(v_1, v_3)$는 연결 되어 있지 않기 때문입니다!

이번에는 $O_2 = (u_1, u_3, u_2) \sim (A, C, B)$의 Matching Order 순서로 서브 그래프 $g_1$에 매칭 시켜 봅시다. 그러면, 매칭이 오른쪽 그림의 순서로 맺어집니다. 그런데, $O_2$에서는 $u_2$를 매칭할 때, $v_4$부터 $v_{1004}$까지 모든 매칭을 검사해야 합니다.

이것은 쿼리 그래프를 매칭 할 때, 매칭 오더를 어떻게 잡느냐에 따라서 매칭을 검사하는 횟수가 크게 달라질 수 있다는 것을 말합니다.

Useless Enumerations

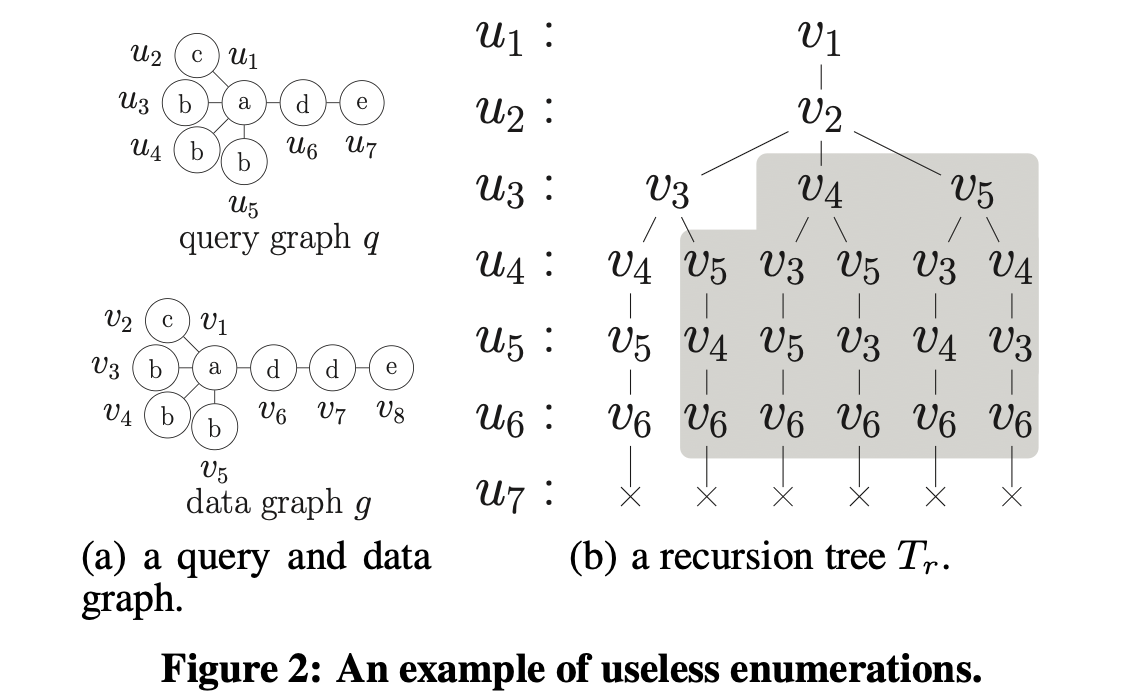
논문에서는 또 다른 예시 쿼리&데이터 그래프로 상황을 설명 합니다. 참고로 여기에서도 쿼리 그래프에 대한 Isomorphism은 존재하지 않습니다!

매칭 오더가 $O = (u_1, u_2, \cdots , u_7)$일 때, 데이터 그래프에서 매칭은 Fig2와 같이 찾게 됩니다.

재귀 트리 $T_r$의 첫번째 경로에서 매칭이 실패한다는 것을 알았습니다. 그리고, 나머지 가지들도 매칭을 확인해보면 모두 실패합니다. 논문에서는 여기에서 아이디어를 제시 합니다!

재귀 트리 $T_r$의 경로를 보면, $- (v_3, v_4, v_5) -$에 대ㄴ 순서만 바뀝니다. 그리고 각 정점은 같은 레이블과 같은 형상(topology)를 가지고 있습니다.

논문은 이런 경우를 쓸모없이 순회(useless enumeration)를 하는 상황이라고 정의 합니다. 그래서 이것을 효율적으로 제거하기 위해 “Neighborhood Equivalence Class(NEC)“라는 개념을 제시합니다. NEC는 비슷한 정점들은 묶어서 처리하고, 불필요한 순열(Permutation)을 미리 제거하여 계산 낭비를 방지하는 것을 목적으로 합니다. 자세한 내용은 뒤에서 더 다루겠습니다.

Neighborhood Equivalence Class (NEC)

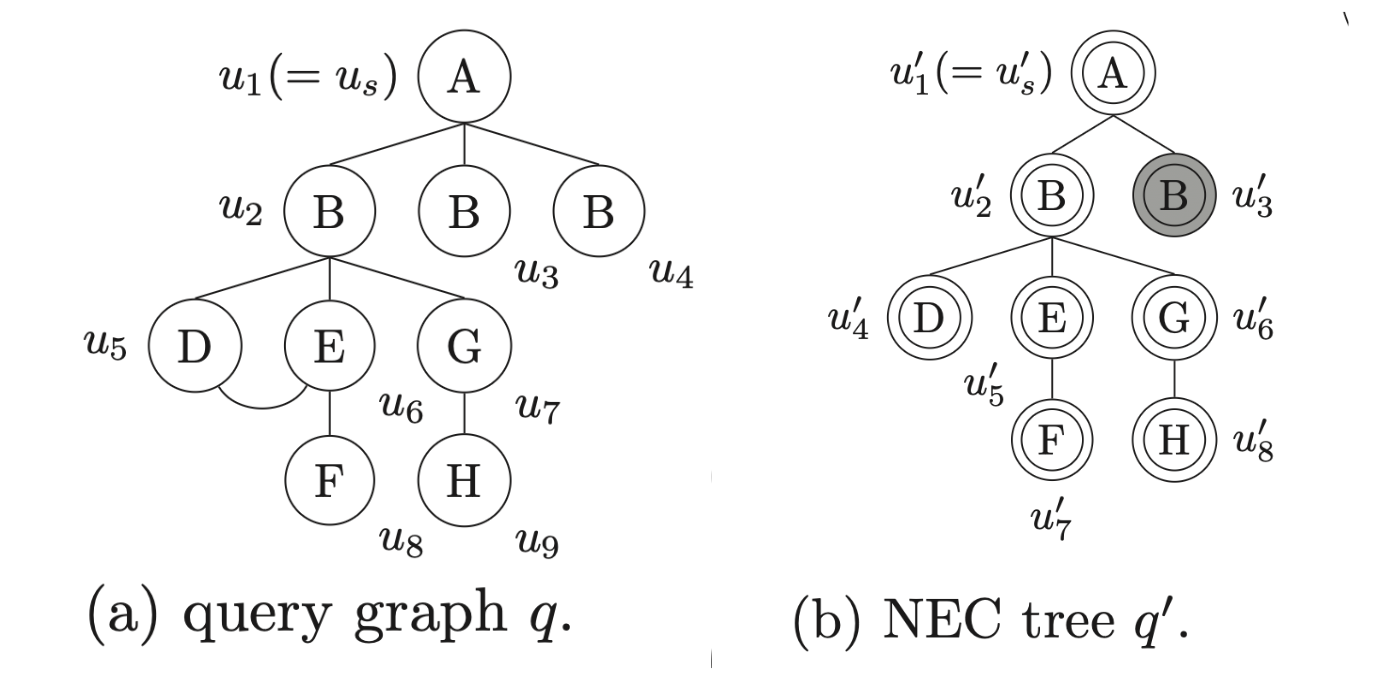
TurboIso는 “쿼리 그래프를 NEC 트리로 바꾸는 작업“을 제일 먼저 수행 합니다. 이 과정은 BFS로 이뤄지며, 그래프 매칭 작업도 쿼리 그래프 $q$가 아니라 NEC Tree $q’$에 대해 수행합니다.

이제 NEC 집합에 대해서 엄밀히 정의해보겠습니다.

If for every embedding $m$ that contains $(u_i, v_x)$ and $(u_j, v_y)$, there exists an another embedding $m’$ s.t.

\[m' = m \setminus \left\{ (u_i, {\color{red} v_x}), (u_j, {\color{blue} v_y}) \right\} \cup \left\{ (u_i, {\color{blue} v_y}), (u_j, {\color{red} v_x}) \right\}\]

then, let $\simeq$ be an “equivalence relation” over all query vertices in $q$, and two query node are $u_i \simeq u_j$.

즉, 두 쿼리 노드에 대해서 그 둘의 매핑된 데이터 노드 $v_{x,y}$를 서로 맞바꿔도 여전히 임베딩 $m’$이 항상 가능하다면, 그 쿼리 노드를 “동치(Equivalent)”라고 하고, 서로 동치인 쿼리 노드를 모은 것이 “NEC” 집합이 됩니다.

앞선 “Useless Enumeration” 예시에서도 봤듯이 NEC 집합 내에서는 그들의 매핑을 서로 맞바꿀 수 있습니다. 그래서 순열(Permutation)의 크기 만큼 방문 순서, 즉, 매칭 $m$이 만들어집니다.

Rewrite query graph to NEC Tree

지금까지 NEC가 왜 좋은지를 설명 했습니다. 그럼 이 NEC Tree를 어떻게 만들어야 할까요? 그리고 어떻게 효율적으로 만들 수 있을까요?

TurboIso는 같은 NEC 집합에 속하는 쿼리 노드들이 아래와 같은 성질이 있다는 것을 발견 합니다.

Let $SP(u_s, u_i)$ be “the set of all shortest paths” from $u_s$ to $u_i$.

If the two query vertices $u_i$ and $u_j$ are in same NEC, then they have same size of shortest path set.

\[\left\vert SP(u_s, u_i) \right\vert = \left\vert SP(u_s, u_j) \right\vert\]

참고로 집합 등호인 $SP(u_s, u_i) = SP(u_s, u_j)$로 표현하지 않는 이유는 Shortest Path에서 마지막에 방문하는 노드가 $u_i \ne u_j$로 서로 다르기 때문입니다. 그 직전까지는 모두 같은 Shortest Path를 갖습니다.

학부 알고리즘 수업에서 $u_s$에서 시작해 $u_i$에 도달하기 위한 최단 경로를 찾고자 한다면, BFS 검색을 사용해야 했습니다. (Weighted Graph 였다면, 다익스트라를 사용합니다.)

그래서 NEC Tree를 구성할 때, BFS 탐색을 사용합니다!

그리고 NEC Tree $q’$에서 부모-자식 노드 사이 관계가 있다면, 그것은 쿼리 노드에서 부모 NEC 노드의 모든 정점은 자식 NEC 노드의 모든 정점과 완전 연결 되어 있어야 합니다.

NEC 트리는 쿼리 그래프를 계층적으로 분해한 구조이기 때문에, 당연하게 받아들일 수 있는 명제 입니다.

그리고 어떤 NEC 트리의 노드 $u’$에 대해, 이 NEC를 이루는 본래 쿼리 노드의 목록은 아래와 같이 표기 합니다.

\[u'.NEC = \left\{ u \in V(q) \, : \, u \simeq u' \right\}\]

예를 들어, $u’_1.NEC = \left\{u_1\right\}$이 되고, $u’_3.NEC = \left\{ u_3, u_4 \right\}$가 됩니다.

이때, 쿼리 그래프 $q$를 NEC 트리 $q’$로 변환하면서, 보존되지 못한 그래프 엣지들이 존재합니다. 이들을 “non-tree edge”라고 합니다. non-tree 엣지들은 따로 기록해뒀다가 NEC 트리 기반으로 찾은 매칭을 검증하는 과정에서 활용한다고 합니다.

Candidate Region $CR(u)$

TurboIso는 빠른 쿼리 매칭을 위해 데이터 그래프 위에 Candidate Region $CR$을 정의합니다.

이 Candidate Region은 “Embedding을 가질 것으로 기대되는 데이터 그래프의 영역“입니다.

존재성이 기대되는 영역이기 때문에, 만약 Embedding이 존재한다면, 이 영역 안에서 반드시 존재합니다. 그리고 Embedding이 존재하지 않는다면 Candidate Region 내에서 Embedding을 찾을 수 없습니다.

결국 Embedding 존재 여부와 상관 없이, 정의한 Candidate Region 위의 데이터 그래프만 탐색하기 때문에, 데이터 그래프 전체를 탐색할 필요가 없어지고 이것은 검색 공간을 크게 줄여줍니다!

표기는 $CR(u)$라고 하고, “쿼리 노드 $u$를 루트 노드로 했을 때, 만들어지는 Candidate Region”라고 합니다.

How to construct Candidate Region?

TurboIso는 Candidate Region을 아래의 과정을 통해 구축 합니다.

1. 쿼리 그래프 $q$를 NEC 트리 $q’$로 변환 합니다.
2. NEC 트리의 루트 노드 $u_s$에 대응되는 데이터 그래프 정점 $v_s$를 찾습니다.
   • 이때, $u_s$에 대응되는 $v_s$는 여러개 존재할 수 있습니다.
3. $v_s$를 루트로 삼아 DFS 탐색 합니다.
   • 쿼리 트리의 구조와 일치할 수 있는 서브 그래프들을 수집합니다.
   • 이게 Candidate Region이 됩니다!

Candidate Subregion

“Candidate Subregion”은 Candidate Region을 구하는 과정에서 계산하는 중간 결과들 입니다.

Candidate Subregion은 NEC 트리의 각 노드에 candidate 데이터 노드 정보를 담고 있습니다.

그리고 당연하게도 모든 Candidate Subregion을 모으면, Candidate Region이 됩니다!!

\[\text{Candidate Region} = \bigcup \text{Candidate Subregion}\]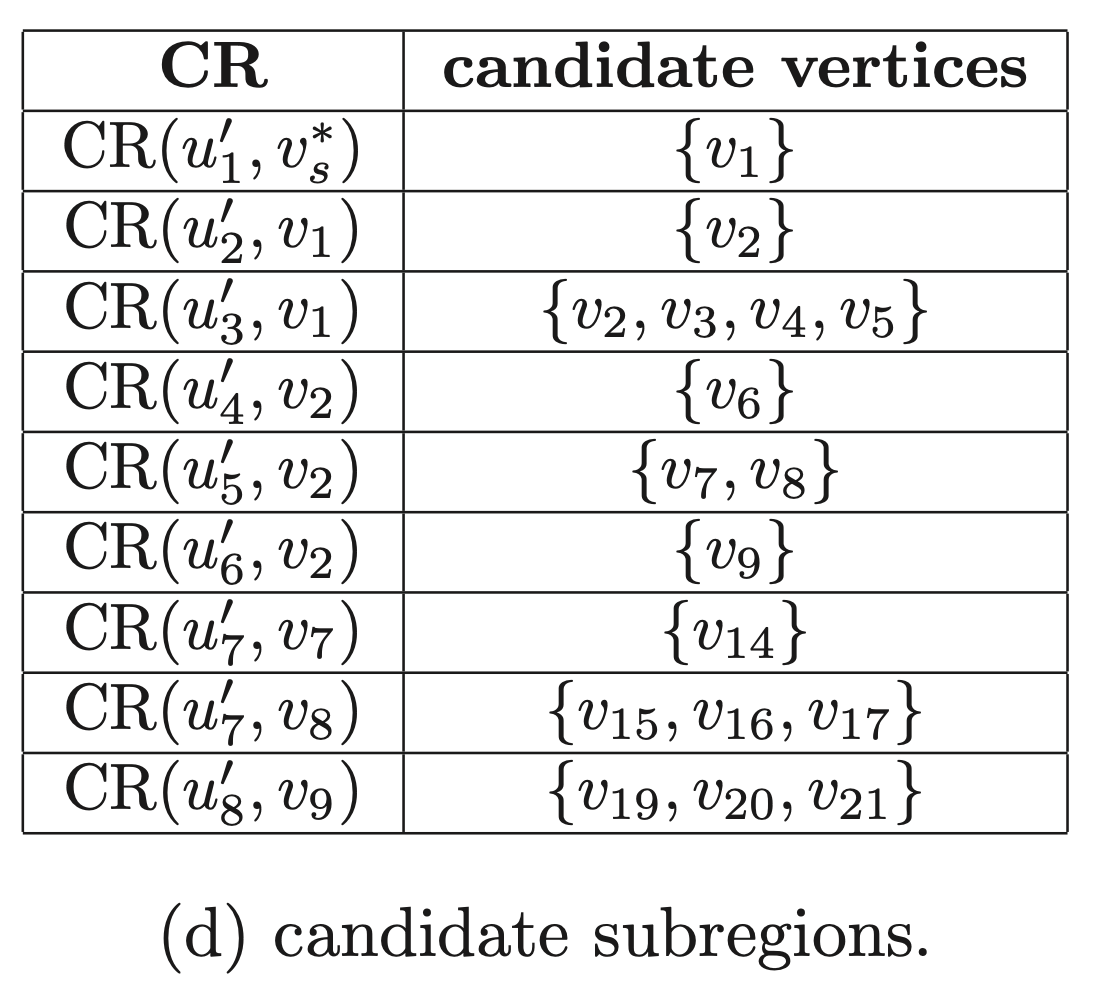

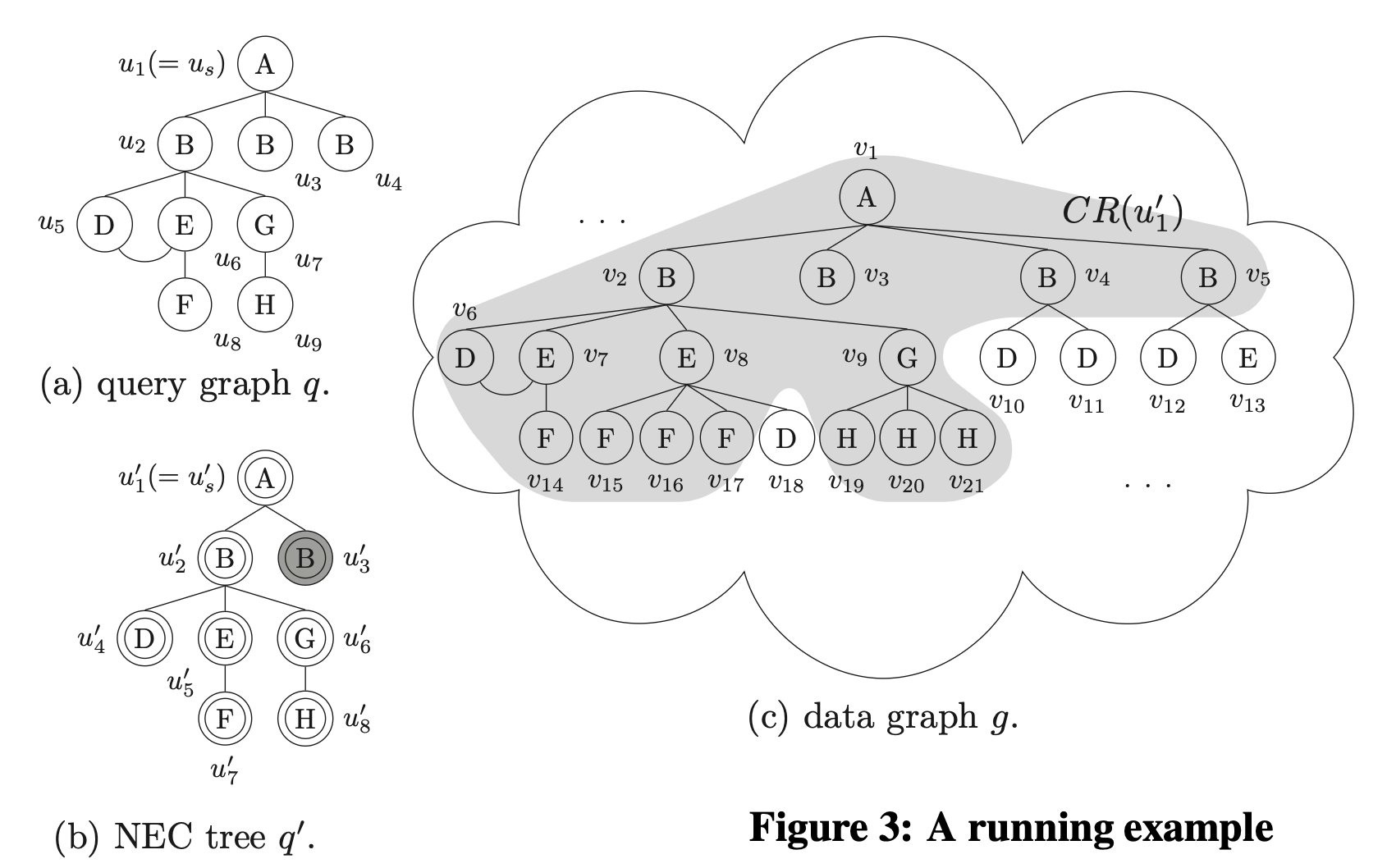
위의 표는 Fig3에 제시된 Candidate Region을 구성하는 Subregion 정보 입니다.

Candidate Subregion을 명확하게 정의해보겠습니다.

$CR(u’, v)$에서 각 항목의 의미는 아래와 같습니다.

• $u’$ = NEC 트리에서 한 쿼리 노드
• $v$ = 데이터 그래프 상의 한 노드
• $CR(u’, v)$는 아래 조건을 만족하는 데이터 노드의 집합 $\left\{ v’ \right\}$
  • $v’$는 $v$의 DFS 트리에서의 자식 노드여야 함.
  • $u’$까지 가는 경로상의 모든 NEC 노드가, $v’$까지 가는 경로상의 모든 데이터 노드와 매칭이 있어야함.
    • 즉, $u’_s \rightarrow u’$ 트리 경로와 $v_s \rightarrow v’$ 경로가 구조적으로 매칭 되어야 함.
  • $u’$의 서브트리가 Candidate Subregion으로 분류된 $v’$의 서브 트리와 구조적으로 매칭 되어야 함.

정의를 곁들여서 다시 수학적으로 표현해보면

\[CR(u) = \bigcup_{u' \in V(q'), v \in V(g)} CR(u', v)\]

TurboIso 논문의 Fig3를 기준으로 Candidate Subregion의 일부를 구해봅시다.

\[CR(u'_2, v_1) = \left\{ v_2 \right\}\]

그 이유는 $v_2$만 $u’_2$의 서브트리 구조와 일치 하기 때문입니다.

같은 $B$-label이지만, $v_3$, $v_4$, $v_5$는 서브트리 구조가 다르므로 제외됩니다.

\[CR(u'_3, v_1) = \left\{ v_2, v_3, v_4, v_5 \right\}\]

$v_3$, $v_4$, $v_5$는 서브트리 구조가 같으니 포함됩니다.

그런데, $v_2$도 Candidate Region으로 포함 됩니다! 왜냐하면, $u’_3$의 서브트리 구조가 존재하기만 하면 되는데, $u’_3$는 서브트리가 없습니다. 그런데 emptyset($\emptyset$)은 모든 집합에 포함되므로

\[\emptyset \subseteq \text{subtree}({v_3})\]

$v_2$로 Subregion에 포함 됩니다!

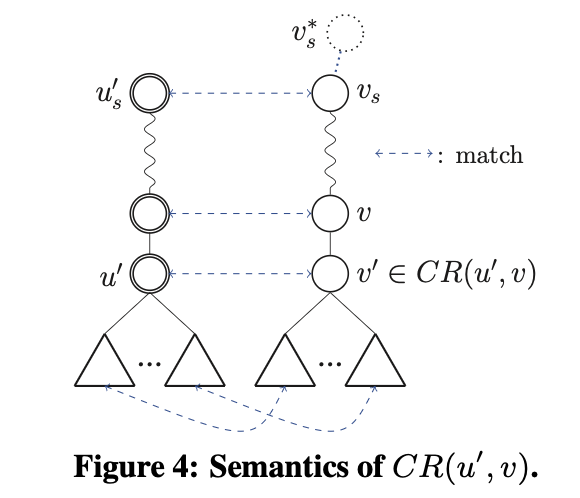
그리고 데이터 그래프에 가상 노드인 $v^\ast_s$를 추가합니다. 이것은 $u’_s$의 매칭 후보인 데이터 정점 $v_s$를 저장하기 위해, 추가한 가상의 노드 입니다.

$v^\ast_s$가 없고, $v_s$가 어떤 다른 부모 노드와 연결된 상황이었다면 $v_s \rightarrow v$의 경로를 엄밀히 정의하기 어렵기 때문입니다.

Explore Candidate Region

Degree-based filtering

NEC 노드 $u’$과 데이터 노드 $v$가 주어졌을 때, $CR(u’, v)$에 속하는 $v’$를 빠르게 구하기 위해 degree 기반으로 필터링을 먼저 한다고 합니다.

만약, $(v, v’) \in E(g)$인 $v’$ 중에서 $\deg (v’) < \deg (u’.NEC[1])$인 노드라면, 해당 데이터 노드 $v’$는 $CR(u’, v)$에 포함될 수 없습니다. 왜냐하면, $u$의 자식 중에 매칭 되지 않는 녀석이 적어도 하나 존재하기 때문입니다.

논문에서는 아래와 같이 예시를 제공 합니다.

• $\deg (u_1) = 3$
• $\deg (u’_1) = 2$

인데, $\deg (v_1) = 4$이므로 $v_1$은 $u’_1.NEC$가 될 가능성이 있습니다.

\[\deg (u_1) = \deg (u'_1.NEC[1]) \le \deg (v_1) \quad \rightarrow \quad \text{possible to belong CR!}\]

Neighborhood Label Frequency (NLF) Filtering

TurboIso는 NLF Filter를 적용해 $CR(u’, v)$에 포함될 수 있는 $v’$를 필터링 합니다.

NLF Filter는 TreeSpan(2012) 논문에서 “Neighborhood Aggregates”라는 이름으로 제시된 필터링 방식입니다. 이름이 무서워서 그렇지 아이디어는 정말 간단합니다 ㅋㅋ

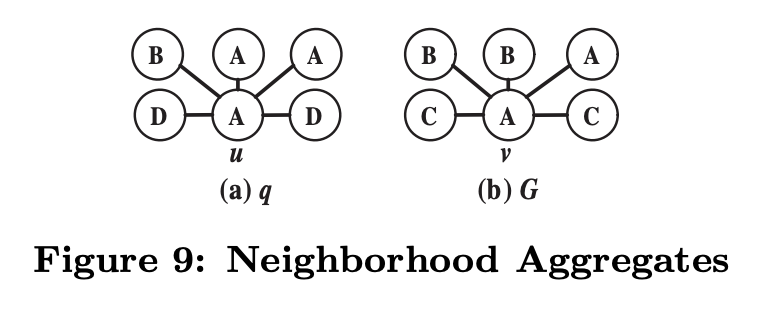
Neighborhood Aggregates $N(v, g)$는 노드 $v$와 인접한 노드들의 Label의 빈도수를 센 값입니다. 예시를 들어서 살펴보면,

Let $(L_1, L_2, L_3, L_4) = (A, B, C, D)$,

\[N(u, q) = (2, 1, 0, 2)\] \[N(v, G) = (1, 2, 2, 0)\]

쿼리 노드 $u$와 데이터 노드 $v$ 두 노드가 매칭되기 위해서는 아래의 조건이 만족 되어야 합니다.

둘의 Neighborhood Aggregates $N(u, q) = (x_1, \dots, x_n)$, $N(v, G) = (y_1, \dots, y_n)$에 대해서

\[\forall i, x_i \le y_i\]

를 만족한다면, 두 노드는 매칭될 가능성이 있습니다. 만약 어느 한 레이블이라도 $x_i > y_i$인, 즉 특정 레이블을 가진 노드와 덜 연결되어 있다면, 쿼리 노드 $u$아 데이터 노드 $v$는 매칭될 수 없습니다.

논문에는 이렇게 쓰진 않지만, 저만의 표현으로 적어보자면

\[N(u, q) \le N(v, G)\]

조건을 만족해야, 매칭이 가능 합니다.

TurboIso 논문에서는 아래와 같이 기술합니다.

[NLF Filter (TurboIso ver)]

For every distinct label $l$ of adjacent vertices of $u$, check if

\[\left\vert adj(u, l) \right\vert \le \left\vert adj(v, l) \right\vert\]

TurboIso는 Candidate Subregion을 계산하기 위해 NLF Filter를 적용합니다. 논문의 Algo3에 이 부분이 코드로 나와 있습니다.

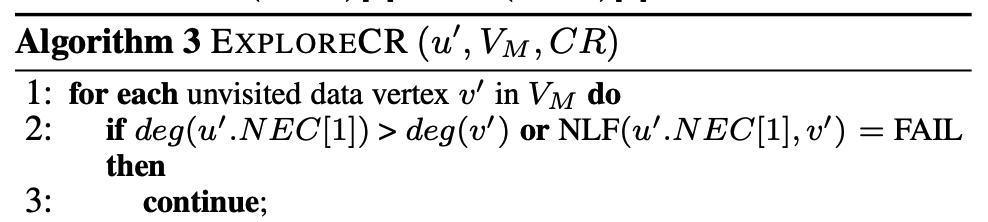
DFS Traversal

$u’$와 $v’$가 Degree 조건과 NLF Filter 조건을 만족한다면, 이제 서브그래프에 대해 구조적으로 매칭 되는지를 확인 합니다.

쿼리 노드 $u’$의 자식 노드 $u’_c$들을 순회하면서 재귀적으로 Candidate Region 탐색을 진행합니다.

이때, 자식 노드 $u’_c$를 순회하는 순서는 $\left\vert adj(v’, L(u’_c)) \right\vert$가 작은 순서부터 큰 순서로 순회 합니다. 이것은 $v’$와 인접한 노드 중에서 가장 적은 빈도를 가진 레이블과 일치하는 자식 노드부터 순회하게 됩니다.

만약, 자식 노드에 대해서 ExploreCR() 한 결과가 실패 였다면, $v’$ 노드는 $u’$의 Candidate Region이 될 수 없습니다.

이때는 ExploreCR() 과정에서 찾은 $u’_c$와 $v’$ 사이에 Candidate Region을 구축할 수도 있습니다. 즉, $CR(u’_c, v’) \ne \emptyset$라는 것이죠. 하지만, $v’$는 $u’$와 매칭 되지 않을 수 있습니다!

이런 경우는 $v’$에 대해서 찾은 결과가 모두 무의미 해집니다. 그래서 $CR(u’_c, v’)$ 초기화 해야 합니다. 이것을 수행하는 것이 ClearCR() 함수 입니다.

매칭이 실패했으니 matched = false로 설정하고 순회를 종료 합니다.

만약 매칭이 가능 했다면(matched = true), 데이터 노드 $v’$를 Candidate Subregion $CR(u’, v)$에 추가합니다.

마지막으로, 완성된 $CR(u’, v)$ 집합과 $u’.NEC$ 집합을 비교 합니다.

이때, $CR(u’, v)$로 매핑되는 데이터 노드가 존재하기는 하는데, $u’.NEC$ 집합의 크기보다 작다면, 매핑이 성립하지 않습니다. 왜냐하면, $u’.NEC$에 속하는 노드 중 일부는 매칭 되지 않기 때문입니다.

그래서 $\left\vert CR(u’, v) \right\vert \le \left\vert u’.NEC \right\vert$를 확인하고, 매칭 가능한 노드 수가 부족한다면, (기껏만든) $CR(u’, v)$ 집합을 ClearCR() 처리 합니다.

Candidate Region을 구성하는 전체 흐름을 살펴보면, 요렇습니다!

Candidate Region Data Structure

이제 Candidate Region을 효율적으로 저장하고, 관리하는 자료구조 구현에 대해 살펴봅시다…! 아직도 남은거냐…

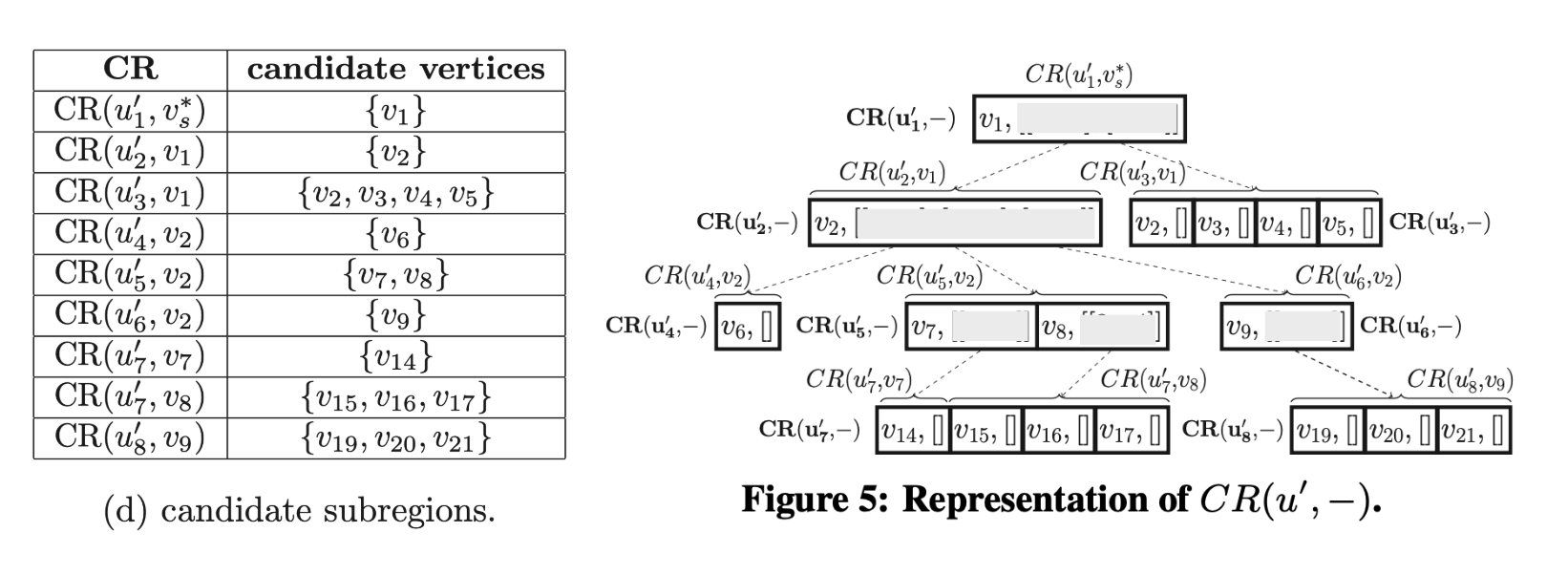
처음에는 이런 표와 같은 형태로 $CR$을 정리 했습니다. 이제 이걸 NEC 트리 $q’$와 같이 그래프 형태로 표현해보면 오른쪽과 같이 표현할 수 있습니다. $CR(u’, v)$가 노드가 되고, 그 안에 $v’ \in CR(u’, v)$의 원소들이 존재 합니다.

$CR(u’, -)$는 “NEC 노드 $u’$와 데이터 노드 $v$에 대한 모든 Subregion을 모은 배열” 입니다. 그래서 $CR(u’_7, -)$를 보면, $CR(u’_7, v_y) \cup CR(u’_7, v_8)$로 이뤄진걸 볼 수 있습니다. 왜냐하면, $u’_7$의 경우 가능한 Candidate Subgraph이 2개 있기 때문입니다. 나머지 노드들은 Candidate Subregion이 하나만 있습니다.

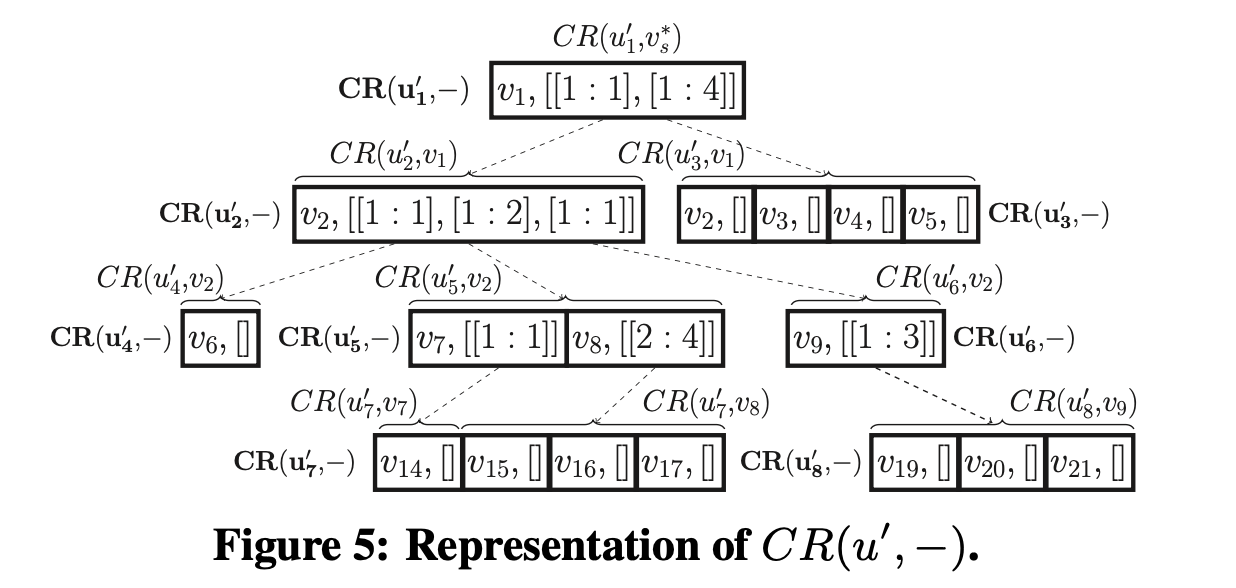
이때, $CR(u’, -)$ 배열 안에서는 어떤 $v$에서 온 것인지 구분 없이 저장합니다. $CR(u’, -)$ 배열에는 $(v’, L)$가 저장 되는데, 매칭 되는 데이터 노드인 $v’$이고, $L$은 “list of ranges $[s, e]$”라고 합니다. 이때, 배열 표현은 inclusive 입니다.

예를 들어, 하나의 $CR(u’, -)$을 코드로 적어보면,

CR_u2_arr = [
   (v2, [[1, 1], [1, 2], [1, 1]]),
]
CR_u7_arr = [
   (v14, []),
   (v15, []),
   (v16, []),
   (v17, []),
]

이때, $L$의 크기는 $u’$의 NEC 자식 노드의 갯수만큼 가집니다. 그래서 자식이 없는 NEC 노드는 L = []로 empty list가 됩니다.

만약 자식이 3개인 NEC 노드($u’_2$)라면, 배열 $L$는 L = [l_1, l_2, l_3]이 됩니다. 이때, $l_i$에는 $[s, e]$로 시작과 끝 값이 저장 되는데, 이것은 하위 NEC 노드에서 이 $v’$과 연결되는 것의 (연결된) 자식이 무엇인지 구분하는 녀석 입니다.

예를 들어, $CR(u’_5, -)$에 있는

• $(v_7, [[1, 1]])$
  • $v_7$의 자식은 $CR(u^\prime_7, -)$의 $v_14$ 입니다.
• $(v_8, [[2, 4]])$
  • $v_8$의 자식은 $CR(u^\prime_7, -)$의 $v_{15}$, $v_{16}$, $v_{17}$ 입니다.

참… 어렵다… 그죠…? ૮(˶ㅠ︿ㅠ)ა

맺음말

내용이 길어져서 포스트를 분리합니다! “Matching Order”에 대한 내용부터는 아래 포스트로 고고!

➡️ TurboIso - Matching Order