Paper Reading: TurboFlux

2025년 저는 데이터베이스 랩에 컨택하여 학부 졸업 연구 주제를 받아서 진행하고 있습니다. 저의 주제는 “Continuous Subgraph Matching”과 관련해 코드를 최적화 하고 개선하는 것으로 그래프 쿼리 관련 논문을 읽고, C++ 코드를 튜닝하고 있습니다. 졸업 마지막 학기에 듣는 수업인데 많은 노하우와 경험을 쌓고 졸업하기를 기대하고 있습니다 ㅎㅎ

Kyoungmin Kim, In Seo, Wook-Shin Han, Jeong-Hoon Lee, Sungpack Hong, Hassan Chafi, Hyungyu Shin, and Geonhwa Jeong. 2018. TurboFlux: A Fast Continuous Subgraph Matching System for Streaming Graph Data.

들어가며

졸업연구를 진행하면서, Symbi(2021)에서 기대만큼의 성능 차이가 잘 보이게 되어서 TurboFlux(2018) 논문에 대해서도 실험을 진행하게 되었습니다. 그래서 논문에 대한 파악이 필요하게 되었는데요! 이 포스트에서 논문을 이해하기 위한 과정을 기록 합니다.

참고로 유튜브에 TurboFlux의 저자가 발표한 10분짜리 영상도 있는데, 처음에 컨셉을 잡는데 도움이 되었습니다! [Youtube]

SJ-Tree

논문에 SJ-Tree(2013)에 대한 내용이 나와서 간단하게 요약합니다! 논문을 이해하는데 곁지식 정도라서 컨셉만 이해하고 넘어갔습니다.

일단 SJ-Tree는 주어진 쿼리 그래프를 작은 서브 그래프로 “분해(decomposition)” 합니다. 분해한 서브 쿼리 사이에는 공통 노드가 있으며, 이후 이것을 기준으로 계층 조인을 수행 합니다.

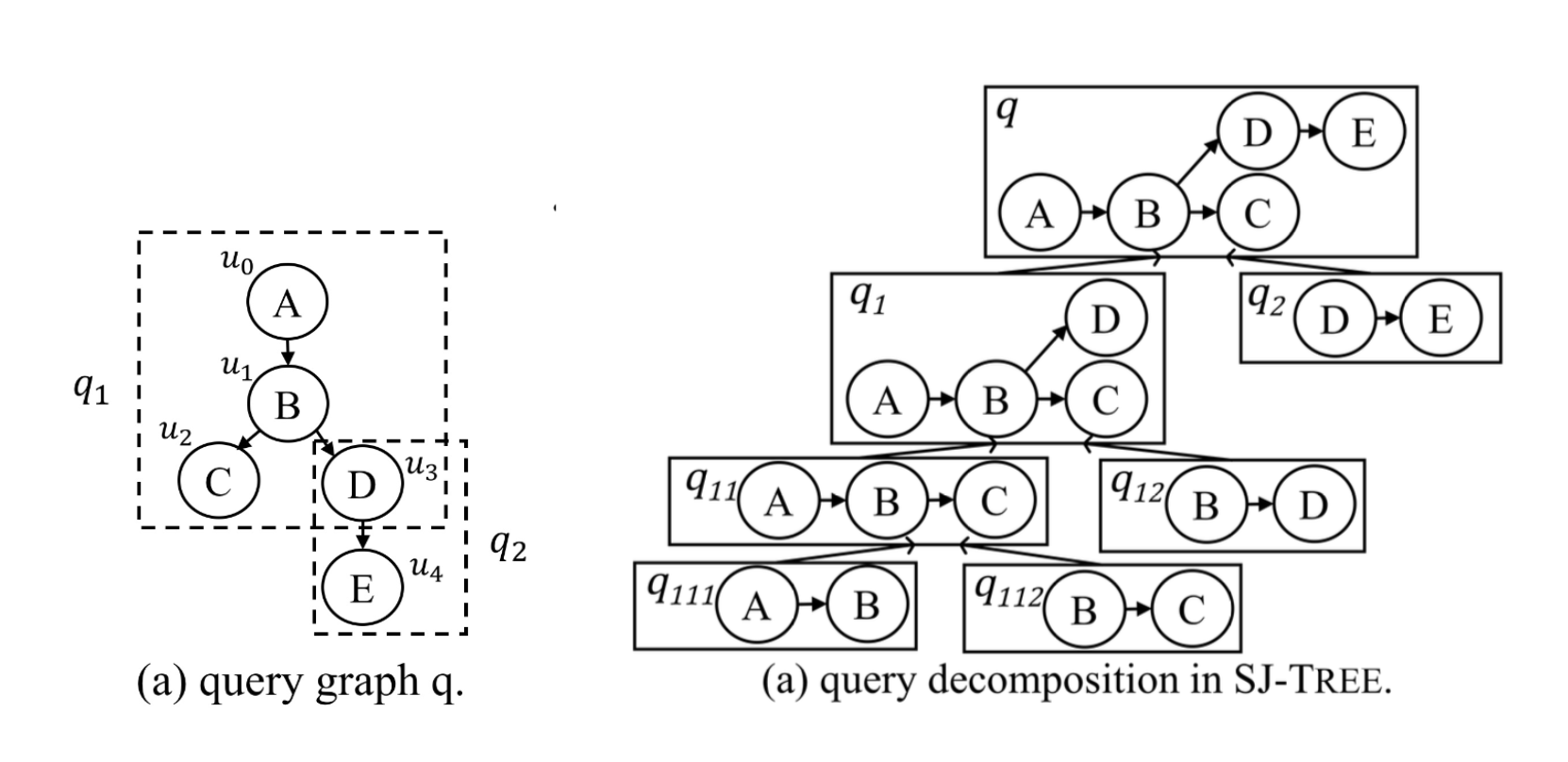
분해로 만들어진 서브 그래프 마다 매칭 결과를 Partial Solution으로 저장합니다. 그리고 업데이트 연산 $\Delta o_i$가 생길 때마다, 이 Partial Solution을 업데이트 하고, 이것을 계층적으로 조인하여 최종 솔루션을 찾아낸다고 합니다. 이런 컨셉에서 “SJ(Subgraph Join)”-Tree의 이름이 유래된 것 입니다.

계층적으로 조인 하는 과정은 아래와 같습니다. 위의 캡처에서 $g_2$ 상황을 기준으로 설명하겠습니다.

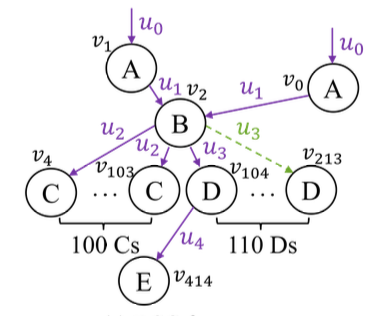
1. 먼저 가장 리프 노드인 $q_{111}$과 $q_{112}$를 계층 조인 하여 $q_{11}$를 구합니다.
   1. 각각이 $q_{111} \Join q_{112} = 2 \times 100 = 200 = q_{11}$이 됩니다.
2. 마찬가지로 $q_{11}$과 $q_{12}$를 계층 조인하여 $q_1$을 구합니다.
   1. $q_{11} \Join q_{12} = 200 \times 110 = 22,000 = q_1$
3. 마지막으로 $q_1 \Join q_2$하여 원본 쿼리 $q$에 대한 매칭을 찾습니다.
   1. 이때는 $q_1 \times q_2 = 22,000$가 아니라, $q = 200$이 됩니다.
   2. 이유는 $B - D$ 연결 중에서 딱 한 경우만 $D - E$ 연결을 가지기 때문 입니다.
   3. 그래서 $q_{111} \times q_{112} \times 1 \times 1 = 200$이 됩니다.

그런데, SJ-Tree의 단점은 아주 큰 공간 복잡도가 필요하다는 것 입니다. 쿼리를 서브 쿼리로 분해하기 때문에, 이 서브 쿼리에 대한 Partial Solution을 유지하는 것만 해도 아주 큰 공간이 필요합니다. 캡쳐에서는 Partial Solution이 $1$ 또는 $200$이라는 숫자로 나왔지만, 실제로는 (해시) 테이블로 관리합니다.

SJ-Tree의 공간 복잡도는 아래와 같다고 합니다.

\[O(\vert V(q) \vert \times \vert E(g) ^ {E(q)} \vert)\]

TurboFlux는 SJ-Tree의 단점을 해결하고자 “DCG(Data Centric Graph)”라는 자료구조를 새롭게 제안 합니다.

이 자료구조는 SJ-Tree 보다 더 작은 공간으로 동작하며, 조인을 기반으로 하는 SJ-Tree와 달리 DCG를 그래프 순회하는 것으로 CSM의 해를 찾아냅니다.

Introduction to Data-centric method

기존의 서브 그래프 매칭은 각 쿼리 노드마다 후보 데이터 노드들을 기억 해두었습니다. 그런데, TurboFlux에서는 반대로 “각 데이터 노드마다 어떤 쿼리 노드가 매칭 가능한지를 저장해보자“고 합니다. 이것이 바로 “Data-centric method” 입니다!

즉, 데이터 노드마다 매칭할 수 있는 “candidate query vertices”를 관리합니다. 그리고 매핑을 계산하는 중간 결과 역시 “data-centric” 방식으로 저장한다고 합니다.

DCG Graph Nodes

이어지는 부분부터 쿼리 그래프 $q$를 사이클을 제거해 쿼리 트리 $q’$로 만듭니다. 만약 쿼리 그래프에 사이클이 있는 경우는 논문의 후반후에 다룰거라고 합니다.

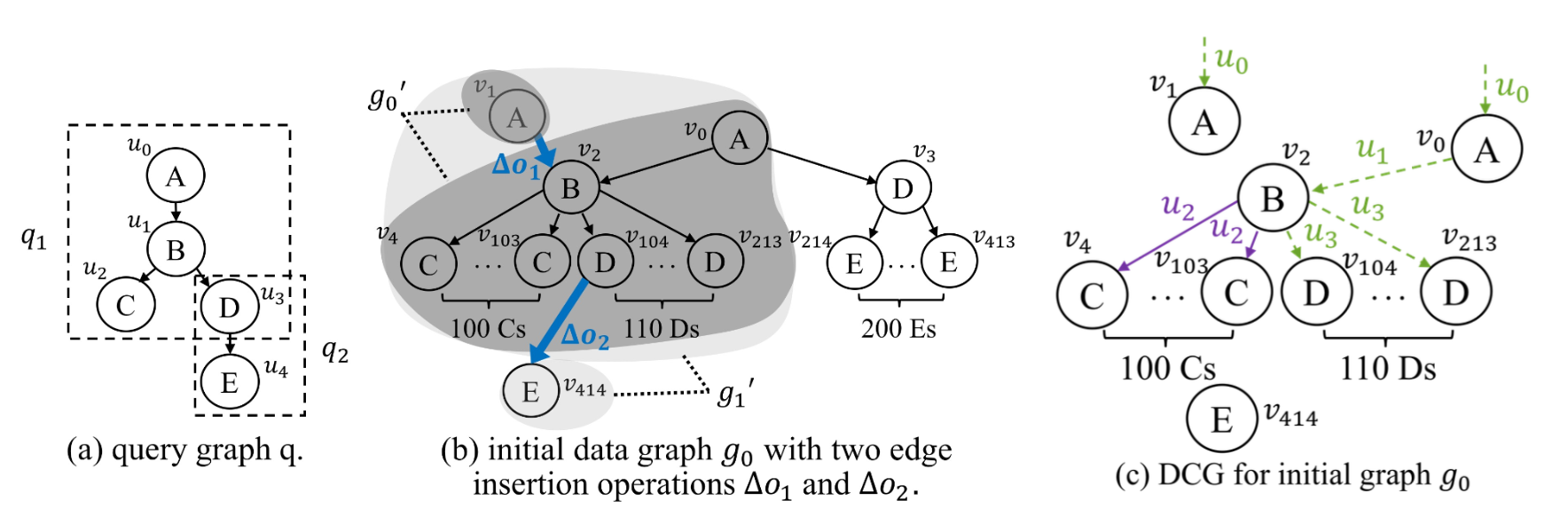
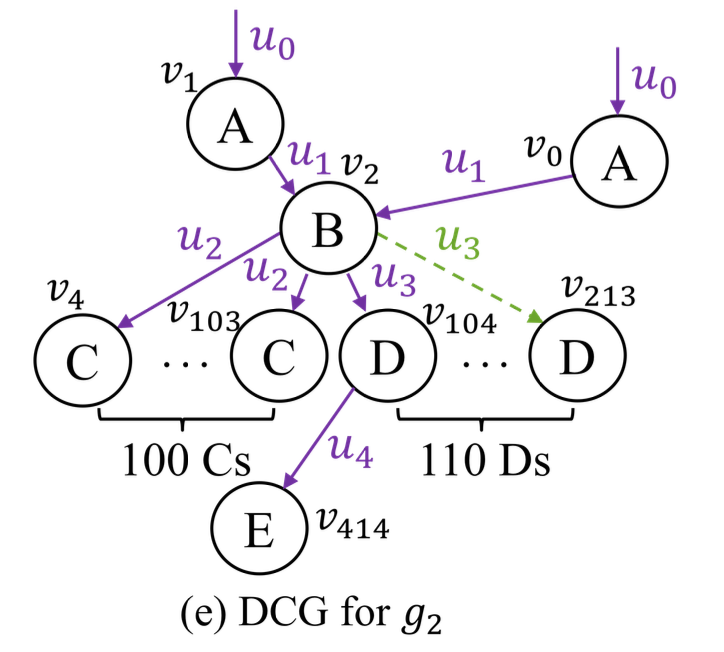
위의 그림은 DCG 그래프의 예시 입니다. DCG는 데이터 중심의 그래프이기 때문에, 데이터 그래프 $g_0$의 노드가 DCG에 모두 존재합니다.

DCG Graph Edges

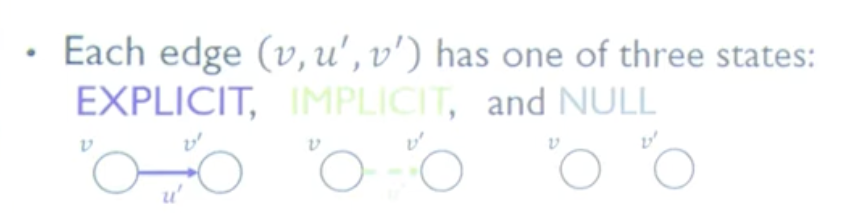논문 저자의 발표 영상에서 가져와서 화질이 좀 안 좋습니다 ㅠㅠ

DCG의 각 엣지는 $(v, u’, v’)$의 형태로 표현 되는데, 이것은 아래 3가지 상태를 가질 수 있습니다.

• Explicit
• Implicit
• NULL

Explicit과 Implicit 둘다 $v’$에 대한 후보 쿼리 노드 $u’$가 존재한다는 것을 나타냅니다. 이때, 후보 쿼리 노드가 존재하려면,

• 데이터 그래프의 시작 노드 $v_s$에서 $v$를 거쳐 $v’$까지 도달하는 경로
• 쿼리 그래프의 시작 노드 $u_s$에서 $P(u’)$를 거쳐 $u’$까지 도달하는 경로

두 경로가 같은 구조(노드 레이블, 거쳐온 노드 갯수와 순서)를 가지고 있음을 의미 합니다.

이것을 아래와 같이 표기할 수 있습니다.

\[\begin{aligned} v_s &\rightarrow v.v' \\ &\equiv \\ u_s &\rightarrow P(u').u' \end{aligned}\]

그리고 Explicit과 Implicit의 차이는

논문 저자의 발표 영상에서 가져와서 화질이 좀 안 좋습니다 ㅠㅠ

$u’$의 모든 서브 트리가 $v’$의 서브 트리와 매칭 된다면, Explicit이라고 분류 하고,

논문 저자의 발표 영상에서 가져와서 화질이 좀 안 좋습니다 ㅠㅠ

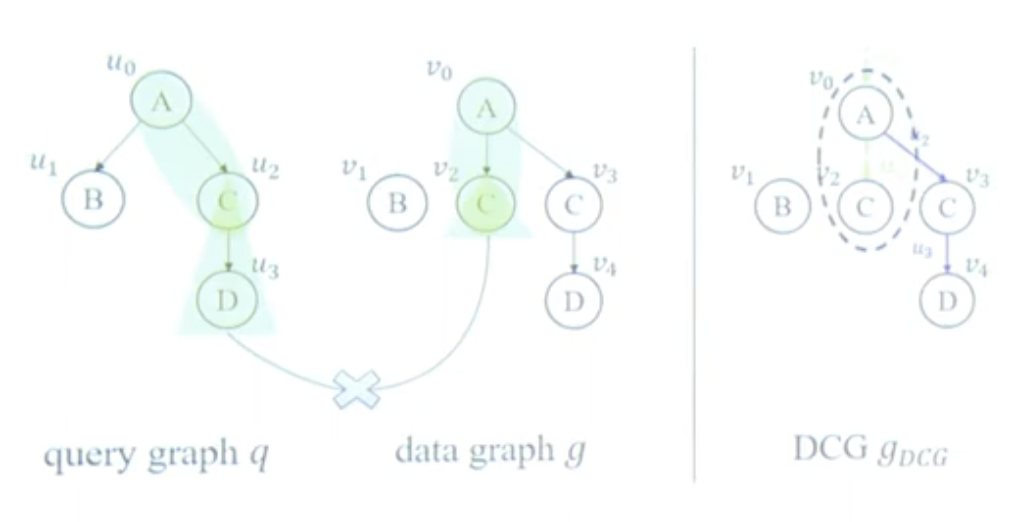
$u’$의 서브 트리 중에 $v’$의 서브 트리와 매칭 되지 않는 것이 있다면, Implicit이라고 분류 합니다.

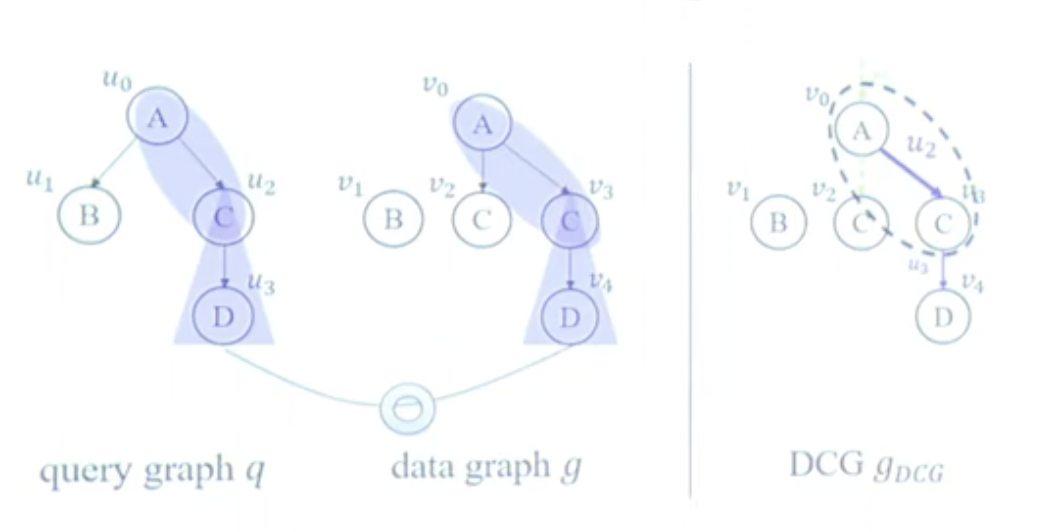
논문의 다이어그램에서는 이를 Edge 색깔로 구분하는데, Explicit이면 보라색 실선, Implicit이면 연두색 점선으로 그려집니다.

참고로 NULL 엣지는 가상의 상태입니다. 이것은 데이터 노드와 매칭 되는 쿼리 노드가 전혀 없거나 아직 매칭 되는 쿼리 노드를 찾지 못 했음을 표현합니다.

Example

다시 캡처를 가져와서 DCG 구조를 이해해봅시다.

먼저 Explicit 엣지부터 살펴봅시다. $u_0 \rightarrow u_1.u_2$ 경로는 $v_0 \rightarrow v_2.v_4$ 경로와 매칭 됩니다. 그리고 $u_2$와 $v_4$ 둘다 서브 트리가 없는 리프 노드 입니다. 따라서, $(v_2, u_2, v_4)$는 DCG에서 Explicit 엣지가 됩니다.

Implicit 엣지도 살펴봅시다. $u_0 \rightarrow u_1.u_3$ 경로와 $v_0 \rightarrow v_2.v_{104}$ 경로와 매칭 됩니다. 그러나, $u_3$에는 서브 트리 $(u_3, u_4)$가 있고, $v_{104}$에는 서브 트리가 없습니다. 따라서, $(v_2, u_3, v_{104})$는 DCG에서 Implicit 엣지가 됩니다. 이는 $v_{104}$가 $u_3$와 부분적으로만 매칭 되며, 추가 검증이 필요함을 의미 합니다.

위의 그림은 매칭이 존재하는 상황 입니다. 데이터 노드의 루트 노드인 $v_s$에 매칭된 $u_0$ 엣지가 “Explicit”이 되면 “Positive 매칭”이 발생합니다!

DCG에서 엣지는 $(v, u’, v’)$ 형태로 표현 됩니다. 그런데, 데이터 노드의 $v_s$가 쿼리 노드의 $u_s$와 매칭 될 때는 가상의 데이터 노드 $v_s^\ast$가 사용 됩니다. 그래서 시작 노드에 대한 매칭은 $(v_s^\ast, u_s, v_s)$로 표현 합니다. 하지만, $v_s^\ast$는 가상의 노드이기 때문에 DCG 그래프에 해당 노드를 저장하거나 시각화 하지는 않습니다.

Compare with SJ-Tree

논문의 초반에 DCG는 SJ-Tree 보다 더 좋은 공간 복잡도를 가진다고 하였습니다. 실제로 논문의 Fig 2를 기준으로 두 자료구조가 저장하는 데이터를 비교해보면,

• DCG of $g_0$
  • 213개의 엣지를 저장
• SJ-Tree of $g_0$
  • 11,311개의 부분 솔루션을 저장

이것은 DCG가 SJ-Tree보다 훨신 적은 공간을 사용하면서도 매칭 정보를 유지할 수 있음을 뒷받침 합니다.

Compare with Query-centric

기존의 쿼리 중심 자료구조(QCG)에서는 각 쿼리 노드 $u$에 대해 매칭 되는 후보 데이터 노드 $v$의 집합을 관리해야 했습니다. 그리고 과정을 진행하다보면, 한 데이터 노드가 여러 쿼리 노드에 매칭 후보로 들어가는 경우가 종종 있었습니다. 이 경우, 해당 데이터 노드 $v$에 업데이트가 발생할 때마다, 그걸 후보 노드로 갖는 모든 쿼리 노드 $u$를 찾아야 했습니다. 이렇게 하려면, “Duplicate Key Index”라는 추가적인 인덱스 자료구조가 필요 했습니다.

DCG 방식에서는 이런 인덱스가 필요 없습니다! DCG 자체가 그래프이고, 데이터 노드 $v$를 기준으로 작성되었습니다. 그리고 데이터 노드 $v$에 업데이트가 발생하면, 그것의 인접 데이터 노드에 대해서만 접근하고 자료구조를 업데이트 하면 됩니다. QCG에서는 서로 다른 캐시 라인(메모리 공간)에 저장된 쿼리의 후보 리스트에 접근해야 했던 것과는 비교 되는 장점 입니다.

세번째 장점으로는 코드 측면에서도 실용적인 장점이 있다고 하는데요. 요건 TurboFlux의 코드와 기존 코드들을 자세히 알고 있어야 와닿는 것 같습니다 ㅇㅅㅇ

Compare with TurboIso

“TurboIso(2013)“도 서브 그래프 매칭 문제를 풀기 위해 고안된 알고리즘 중 하나입니다. 본 포스트에서 살펴보고 있는 “TurboFlux(2018)”의 저자의 선행 연구 입니다!

TurboIso는 “Candidate Subregion”을 정의하고 이것을 트리 구조로 관리합니다. 이 Candidate Subregion은 (1) 도달 경로와 (2) 서브 트리가 모두 매칭 되는 것들만 모았습니다. 그래서 “완전해(complete solution)”입니다.

TurboFlux도 이것을 “Explicit 엣지”라는 개념으로 저장합니다! 그런데, TurboFlux는 “Implicit 엣지”라는 부분해(partial solution)을 저장합니다. 이 부분해들은 (1) 도달 경로 조건은 만족하지만, (2) 서브 트리 매칭을 만족하지 못 합니다. 이들은 적절한 Update Stream $\Delta o_i$이 발생하면, “Implicit”에서 “Explicit”으로 변화할 가능성이 존재하는 후보 매칭 입니다.

	TurboIso	TurboFlux
Complete Solution	Candidate Subregion	Explicit Edge
Partial Solution	-	Implicit Edge

DCG Edge Transition Model

TurboFlux는 DCG 자료구조를 통해 중간 결과(intermediate result)를 저장합니다. 이것은 “Edge Transition Model”라는 매커니즘에 의해 동작하는데요. 데이터 그래프에서 엣지 추가/삭제가 발생 했을 때, 이것이 Positive/Negative Match에 기여하는지를 효율적으로 판단합니다.

엣지 업데이트가 발생할 때마다, 전체 서브 그래프를 전탐색 하는 것은 비효율적입니다. 그래서 이미 구축된 DCG를 기반으로 업데이트를 수행해야 하는데, 이것에 대한 동작 규칙을 적은 것이 “Edge Transition Model” 입니다.

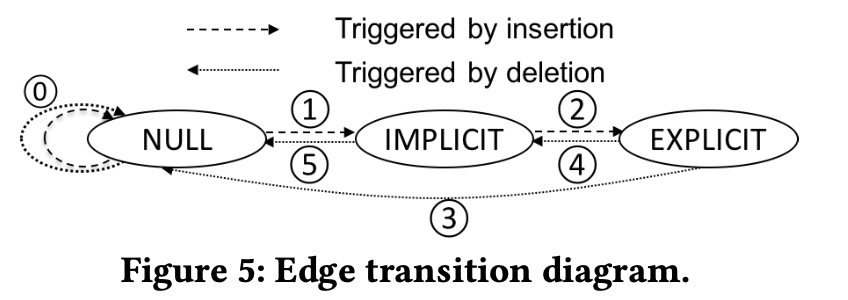
논문은 5가지의 전이 규칙을 정의하고 이것을 엣지 업데이트가 일어날 때마다 호출합니다.

Transition 0: NULL -> NULL

엣지 업데이트가 발생 했지만, 엣지의 상태가 변경되지 않고, 그대로 NULL인 경우 입니다. 즉, 아무것도 일어나지 않는 상황 입니다.

[Case 1]

데이터 그래프에 데이터 엣지 $(v, v’)$가 삽입/삭제 되었지만, 이 엣지가 쿼리 그래프의 어떤 엣지 $(u, u’)$와도 매칭되지 않았습니다.

[Case 2]

데이터 엣지가 $(v, v’)$가 쿼리 엣지 $(u, u’)$와 매칭 됩니다.

DCG에서 $(v, u’, v’)$인 엣지가 존재하지 않고, 부모 노드에 대해서도 $u$와 $v$ 노드가 서로 매칭 되지 않습니다.

이 경우는 부모 노드끼리 매칭 되지 않는 상황이므로, 자식 노드 사이의 업데이트가 발생할 수 없습니다. 따라서, NULL 상태로 유지 됩니다.

이때, NULL 상태는 어디에도 저장되지 않는 가상의 상태임에 유의합니다.

Note that NULL edges are hypothetical edges in order to explain the edge transition … Thus, we do not store edges whose states are NULL in the DCG.”

그래서 NULL -> NULL 전이는 어떤 상태를 바꾸는 것이 아니라, 들어온 엣지 업데이트를 “무시 해도 된다”라는 조건을 체크하는 것 입니다.

Transition 1: NULL -> Implicit

[Case 1]

새로운 엣지 $(v, v’)$가 추가 되었을 때, 이 엣지와 매칭되는 쿼리 엣지 $(u, u’)$가 존재합니다.

그리고, DCG에서 부모 노드 $v$가 $u$ 노드와 매칭을 갖고 있다면, 이를 바탕으로 $(v, u’, v’)$라는 새로운 엣지를 Implicit 상태로 전이 합니다.

뒤에 나오겠지만, 이것은 Implicit 엣지를 저장하는 bitmap에 해당 위치를 false -> true로 전환하는 것을 말합니다.

[Case 2]

DCG의 엣지 $(v, u’, v’)$가 Implicit으로 전이 되었을 때, 그에 따라 $v’$의 이웃과 $u’$의 자식들 사이에도 새로운 매칭 생길 수 있습니다. 그래서 이 전이 과정을 이웃 노드에도 전파합니다.

DCG의 부모 엣지가 “Implicit”으로 전이 되었다면, 자식 노드 $v’$의 자식 노드(손자 노드) $v’‘$와 쿼리 엣지에서의 자식 노드 $u’’$ 사이에 매칭이 존재하는지 확인합니다. 만약 매칭이 존재한다면, DCG 엣지에서 $(v’, u’’, v’’)$ 상태를 Implicit으로 전이 합니다.

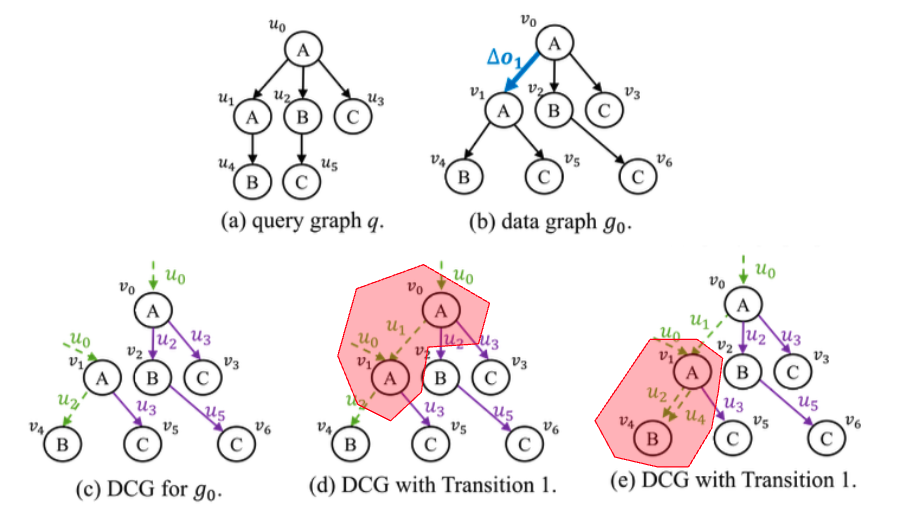
논문의 Fig 4. 다이어그램에서 NULL -> Implicit의 예시를 볼 수 있습니다. 엣지 업데이트 $\Delta o_1$이 발생하면서, $(v_0, u_1, v_1)$ 엣지가 NULL -> Implicit로 전이합니다(Fig4-(d)). 그리고, 이 전이에 의해 $(v_1, u_4, v_4)$ 엣지도 NULL -> Implicit으로 전이 합니다. DCG에서 $v_4$ 노드는 $u_2$와 $u_4$, 2개 쿼리 노드에 대해 Implicit 매칭이 존재하게 됩니다.

Transition 2: Implicit -> Explicit

이 전이는 부분해(Implicit)이 완전해(Explicit)으로 확정되는 규칙을 다룹니다!

[Case 1-1]

DCG 엣지 $(v, u’, v’)$가 NULL -> Implicit로 전이 했을 때, 쿼리 노드 $u’$가 자식이 없는, 리프 노드라면 해당 DCG 엣지를 “Explicit”으로 전이 한다.

[Case 1-2]

DCG 엣지 $(v, u’, v’)$가 NULL -> Implicit로 전이 했을 때, DCG에서 $v’$가 Explicit 엣지를 가지는데, 그들의 쿼리 노드 레이블 $u’‘$가 모두 $u’$의 자식 노드들의 것이 모두 존재한다면, 부모 엣지인 $(v, u’, v’)$의 상태를 “Explicit”으로 전이 한다.

[Case 2]

DCG 엣지 $(v, u’, v’)$가 Implicit -> Explicit으로 전이 되었을 때, 그것의 부모 노드 $v$가 자식들에 대한 서브 트리 매칭을 전부 만족하게 될 수 있습니다! 그러면, $v$로 들어오는 Implicit 엣지들도 모두 Explicit으로 전이할 수 있습니다!

이 경우는, 전이의 전파가 역방향(자식 -> 부모) 방향으로 일어납니다! NULL -> Implicit에서는 전이의 전파가 순방향(자식 -> 부모) 방향으로 일어났던 것과 비교 됩니다.

Transition 3,4,5 (Edge Deletion)

나머지 전이 규칙은 엣지 삭제에 대한 경우 입니다.

[Explicit -> NULL]

데이터 그래프에서 엣지 $(v, v’)$가 삭제 되었습니다. 이 엣지가 쿼리 엣지 $(u, u’)$와 매칭 되었고, DCG에서 $(v, u’, v’)$ 엣지가 Explicit 상태였다면, 이 엣지는 더이상 유효하지 않으므로, Explicit -> NULL로 전이 됩니다.

DCG에서 $(v, u’, v’)$ 엣지가 NULL로 전이 되면서, $v’$의 자식 노드들과 부모 노드들에 대한 핸들링이 필요합니다.

[Explicit/Implicit -> NULL]

부모 노드가 $v’$인 DCG 엣지 $(v’, u’’, v’’)$ 중에서 원래 매칭을 맺었던 쿼리 노드 $u’$와 연결되었던 쿼리 노드 $(u’, u’’)$와 매칭이 있었다면, 이것을 Explicit/Implicit -> NULL로 전이 합니다. (경로가 끊어지기 때문에, 완전히 NULL로 전이 합니다.)

[Explicit -> Implicit]

$v’$를 자식 노드로 갖는 DCG 엣지 $(v, u, v’)$ 중에서 해당 엣지가 “Explicit” 상태 였다면, 이 엣지의 상태가 “Implicit”으로 전이 합니다. 서브 트리 매칭이 깨지기 때문입니다!

[Implicit -> Implicit]

$v’$를 자식 노드로 갖는 DCG 엣지 $(v, u, v’)$ 중에서 해당 엣지가 “Implicit” 상태 였다면, 이 엣지의 상태는… 그대로 “Implicit”로 남아있습니다! 애초에 서브 트리 매칭이 성립하지 않았기 때문입니다.

Edge Logic EL()

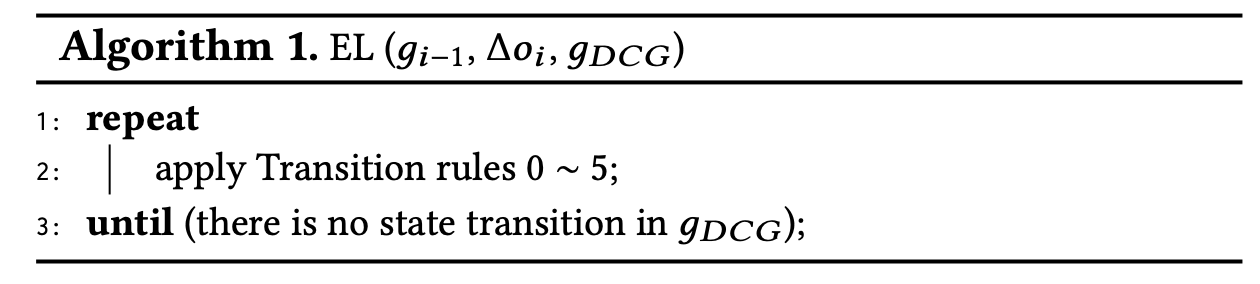
EL() 함수는 엣지 업데이트가 발생할 때마다 호출되는 함수로, 데이터 그래프 $g$, 그래프 업데이트 $\Delta g$, DCG $g_{DCG}$ 정보를 바탕으로 엣지의 상태 전이를 수행하는 함수 입니다.

이 과정은 어디상 상태 전이가 발생하지 않을 때까지 반복 됩니다.

전이 모델의 단순한 구현은 실제 환경에서 성능 문제가 있었다고 합니다. 그래서 실제 구현에서는 효율적인 동작을 위해 여러 테크닉들을 적용 했다고 합니다.

TurboFlux Algorithm

이 문단에서는 TurboFlux의 전체 과정을 단락 별로 살펴봅니다.

Choose Start Q Vertex

TurboFlux는 매칭을 가장 “효율적으로 시작할 수 있는” 정점 $u_s$를 고르기 위해, 선택도(selectivity)를 정의하고, 이를 기준으로 판단 합니다.

1. 가장 좁은 쿼리 엣지를 탐색

쿼리 그래프의 엣지 $(u, u’)$ 중에서 데이터 그래프와 매칭 되는 엣지가 가장 적은 것을 찾습니다. 이렇게 하는 이유는 좁근 조건에서 시작해야 탐색의 가지수가 줄어들기 때문입니다.

2. 가장 좁은 엣지에서 쿼리 노드를 선택

엣지 $(u, u’)$를 이루는 두 노드 중에 하나를 선택해 $u_s$를 정해야 합니다. 이것은 두 노드 중, 데이터 그래프에서 매칭 가능한 정점이 더 적은 것을 선택 합니다.

3. 만약 동률이라면, 차수가 더 높은 정점을 고른다.

만약 $u$와 $u’$에 매칭 되는 정점 수가 동률이라면, 차수(degree)가 더 높은 정점을 고릅니다.

Transform to tree

쿼리 그래프 $q$를 쿼리 트리 $q’$로 변환 합니다.

처음엔 앞에서 선택한 시작 정점 $u_s$ 하나으로 트리를 시작합니다. 그리고 한번에 하나의 엣지를 추가하면서 트리를 확장 합니다.

이때, 엣지는 현재 트리에 포함된 쿼리 정점과 연결된 엣지 중에서, “선택도가 높은 엣지”부터 트리에 포함시킵니다.

이렇게 그래프를 트리로 변환하게 되면, 나중에 트리에 포함되지 못한 “non-tree edge“가 남게 됩니다. 이들은 따로 저장해두어 마지막에 매칭 여부를 확인할 때, 추가 조건으로 사용합니다.

Initialize DCG

DCG를 구축하기 위해 시작 쿼리 노드 $u_s$와 매칭 되는 데이터 노드 쪽 $v_s$를 찾아야 합니다. 이것은 $L(u_s) = L(v_s)$가 되는 데이터 노드를 찾으면 됩니다.

이런 시작 데이터 노드를 찾으면, 이들을 대상으로 BuildDCG() 함수를 트리거 합니다.

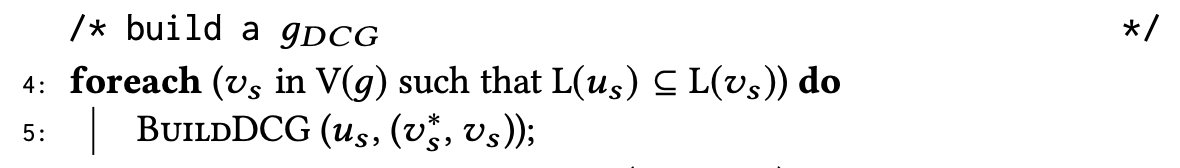
논문의 알고리즘에서는 각 $v_s$마다 DCG가 구축되는 것처럼 보이지만, 실제로는 하나의 DCG만 존재하고, 공통 노드가 있다면 이들은 그 DCG 안에서 연결 되어 있습니다!

Determine Matching Order

DCG가 완성된 후에, 어떤 순서로 쿼리 정점을 처리해야 매칭을 계산하는게 가장 효율적인지 결정해야 합니다.

이 매칭 오더는 정말 중요한데, 매칭 순서에 따라서 중간 결과의 수가 폭발할 수도 있고, 중간 결과가 줄어들어서 알고리즘이 더 효율적으로 동작할 수도 있기 때문입니다.

이제 몇가지 notation이 등장하는데, 매칭 오더

\[mo = <u_{o_1}, u_{o_2}, \dots, u_{o_n}>\]

에 대해서, $T_i$는 그 순서까지의 쿼리 노드들도 만든 “서브 (쿼리) 트리” 입니다.

\[T_i \subseteq q'\]

그리고 이를 바탕으로 매칭 비용을 계산합니다. 매칭 비용은 각 단계 $T_i$에서의 매칭 비용 $c(T_i)$를 모두 더한 값으로 계산합니다.

\[\text{Total Matching Cost} = \sum_i c(T_i)\]

단계별 매칭 비용 $c(T_i)$는 처음 생성한 DCG 그래프를 활용해 계산 합니다. (지금은 전체적인 과정을 훑어보고 있어서, 구체적인 방법은 뒷부분에 다루겠습니다.)

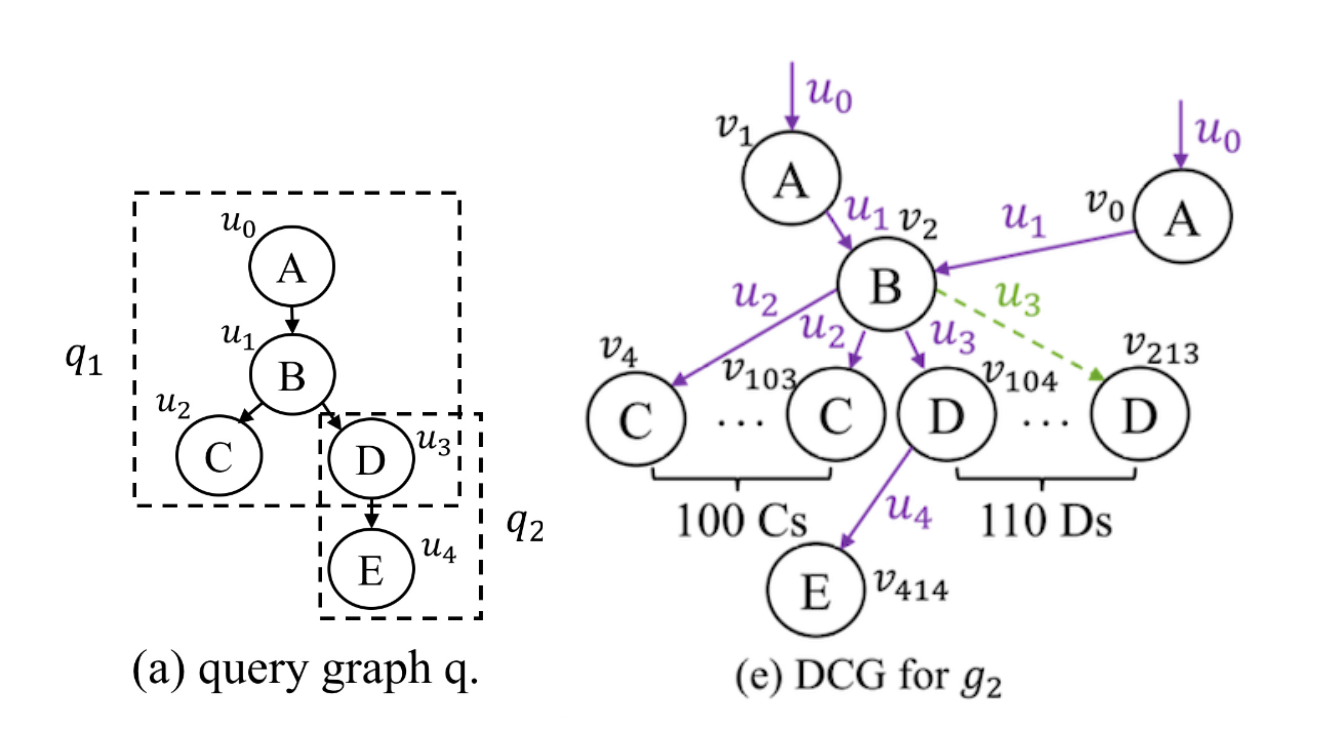
논문에서 제시한 예시인데, 이때는 $mo = <u_0, u_1, u_3, u_4>$가 매칭 오더로 결정된다고 합니다. 그 이유는 DCG $g_2$를 기준으로 할 때, $<u_0, u_1, u_3>$를 서브 매칭 오더로 했을 때, 가능한 매칭 수가 2개로 가장 적기 때문이라고 합니다.

Subgraph Matching on Init DCG

매칭 오더가 결정 되면, 초기 데이터 그래프 $g_0$에 대해 초기에 매칭 되는 서브 그래프를 찾아서 리포트 해야 합니다.

이 과정은 $u_s$와 매칭 되는 $v_s$ 중에서, $(v_s^{\ast}, u_s, v_s)$의 상태가 “Explicit”인 정점들에 대해서 수행 합니다. 이것은 $v_s$는 쿼리 트리에 대해 완전히 매칭된 서브 트리를 가지고 있기 때문입니다.

매핑을 구성하기 위해 $m(u_s) \leftarrow v_s$로 설정 합니다. 그리고 나머지 DCG 노드들에 대해서 SubgraphSearch를 수행합니다. 이 과정은 매칭 오더 $mo$를 따라 수행 됩니다.

과정이 종료되면, $m(u_s) \leftarrow \text{NIL}$를 통해 이전 매핑으로 되돌려 주십니다.

Subgraph Matching for each update stream

TurboFlux는 Continuous Subgraph Matching을 위한 알고리즘 입니다. 따라서, 업데이트 스트림에 대해 적절히 대응해줘야 합니다.

이 과정은 업데이트 스트림이 발생할 때마다, DCG 자료구조를 업데이트 하고, 그 위에서 서브 그래프 매칭 결과를 다시 평가합니다.

이때, 엣지 삽입과 삭제의 처리 방식이 다른데,

[엣지 삽입]

먼저 엣지를 실제 데이터 그래프 $g$에 삽입 합니다. 그 다음 DCG를 갱신하면서 positive match를 찾습니다.

[엣지 삭제]

먼저 DCG에 기반해, 어떤 매칭이 사라질지 판단하고 negative match를 리포트 합니다.
그 다음에 삭제된 엣지를 데이터 그래프 $g$에서도 삭제 합니다.

삽입에서는 “엣지 추가 -> 평가” 순서로 진행했고, 삭제는 “평가 -> 엣지 삭제” 순서로 알고리즘이 수행 되어야 합니다. 엣지를 삭제한 다음에 DCG를 업데이트 하려고 하면, DCG 변경 전 상태를 알 수 없게 되므로 정확한 매칭 변화를 추적하기 어려워지기 때문입니다!

Adjust Matching Order

업데이트 스트림에 의해 데이터 그래프 $g$와 DCG가 계속 업데이트 되고 있습니다. 만약, 어떤 쿼리 경로에 대해서 “Explicit Path”의 수가 크게 변동 한다면, 이것은 각 쿼리 노드에 대한 선택도가 달라졌다는 것을 의미합닌다. 그래서 매칭 오더를 현재 DCG에 맞게 다시 계산함으로써 알고리즘의 효율을 확보할 수 있음을 말합니다.

Overview

논문에서 제공한 TurboFlux의 전체 알고리즘은 아래와 같습니다.

TurboFlux Implementation

Bitmap Representation

TurboFlux는 Implicit 엣지에 대한 정보를 비트맵에 저장합니다. 각 데이터 노드는 “쿼리 그래프의 노드 수 만큼” 비트맵을 가지고, 이 비트맵의 $i$번째 비트는 쿼리 노드 $u_i$에 대응되고, $i$번째 비트맵의 값이 true라면, 해당 데이터 노드와 $u_i$ 노드 사이에 Implicit 엣지가 존재한다고 표시 합니다.

즉, Implicit 엣지는 DCG 자료구조에 직접 저장하지 않고, bitmap에 저장되고 간접 추적 됩니다.

---

DCG는 minimal representation이다?