Bisection Method

수학과 복수전공을 위해 졸업 마지막 학기에 “수치해석개론” 수업을 듣게 되었습니다. 수학과 졸업시험도 겸사겸사 준비할 겸 화이팅 해봅시다!! 전체 포스트는 “Numerical Analysis“에서 확인할 수 있습니다.

Bisection Method

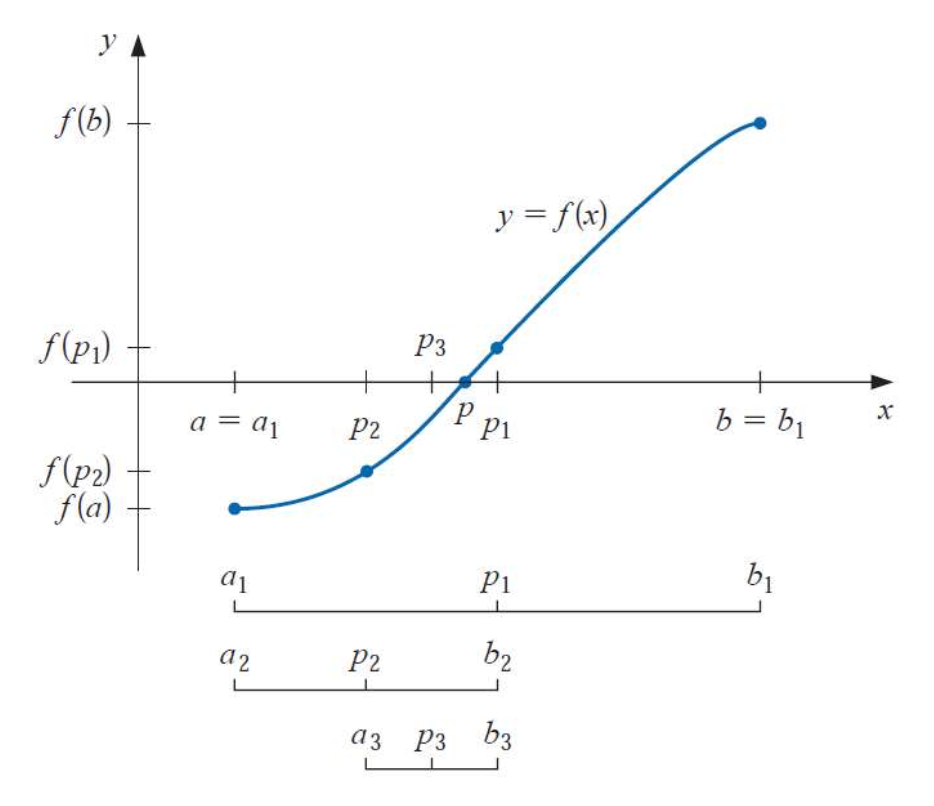
비선형 방정식 $f(x) = 0$의 근을 찾기 위한 수치적 방법 입니다. 특정 구간에서 함수 부호 변화를 이용해 근이 존재 가능한 범위를 점진적으로 좁혀나갑니다.

특징

해를 찾기 위해서 큰 아이디어가 필요하지도 않으며 직관적 입니다.

하지만, 몇가지 단점이 존재하는데, 수렴 속도가 다른 수치적 방법에 비해 느립니다. 뒤에서 다루겠지만, Bisection Method의 수렴 속도는 “선형 수렴(Linear Convergence)”이고, $O(c^n)$으로 표현 합니다. 반면에 “뉴턴-랩슨법“(곧 다룸)은 “이차 수렴(Quadratic Convergence)”의 속도로 수렴 합니다. 이런 관점에서 Bisection Method의 수렴이 느리다고 표현하는 것 입니다.

Error Bound

Supp. that $f \in C[a, b]$ and $f(a)f(b) < 0$.

The Bisection method generates a sequence $\left\{ p_n \right\}_{n=1}^{\infty}$ approximating a zero $r$ of $f$ with

\[\| p_n - r \| \le \frac{b-a}{2^n}, \quad n \ge 1\]

이 명제는 Bisection Method롤 $n$번 수행 했을 때의 오차의 상한에 대해 보장 합니다. 오차의 상한은 $(b-a)/2^n$ 입니다.

Rate of Convergence

Supp. $\left\{ \beta \right\}_{n=1}^{\infty}$ is a sequence known to converge to zero,

and $\left\{ \alpha_n \right\}_{n=1}^{\infty}$ converges to a number $\alpha$.

If there exists a positive constant $K$ s.t. for large $n$,

\[\| \alpha_n - a \| \le K \| \beta_n \|\]

then we say that $\left\{ \alpha_n \right\}_{n=1}^{\infty}$ converges to $\alpha$ with “rate of converge $O(\beta_n)$”.

\[\| p_n - r \| \le \frac{b-a}{2^n}, \quad n \ge 1\]

이분법에서는 수렴 속도를 $O(1/2^n)$라고 합니다.

참고로 “수렴 차수(order of convergence)”라는 개념도 있습니다! 뒤에 뉴턴법으로 root-finding을 할 때, 살펴볼 건데요! 이때, 이분법은 1차 수렴성을 갖고, 뉴턴법은 2차 수렴성을 갖습니다! (자세한 건 뉴턴법을 정리한 포스트에서… link)

Correctness

A solution is “correct within $p$-decimal places”,

if the error is less than $0.5 \times 10^{-p}$.

근사값 $x_n$과 참값 $x$를 $p$번째 자리까지 반올림 했을 때 같은 값이 나오면, 그 근사값은 소수점 $p$자리까지 정확하다고 표현합니다.

예를 들어, $\pi$의 근사값

• 참값: $\pi \approx 3.141592$
• 근사값: $x_n = 3.1415$

그리고 두 값을 3번째 자리까지 반올림 하면

• 참값: $\pi \approx 3.141592 \rightarrow 3.142$
• 근사값: $x_n = 3.1415 \rightarrow 3.142$

따라서 두 값이 같으므로 근사값은 참값과 소수점 3자리까지 정확함.

맺음말

이어지는 포스트에서는 다른 접근 방법들을 살펴봅니다.

• Fixed-point Method
• Newton’s Method
• Secant Method