Fixed-point Method

수학과 복수전공을 위해 졸업 마지막 학기에 “수치해석개론” 수업을 듣게 되었습니다. 수학과 졸업시험도 겸사겸사 준비할 겸 화이팅 해봅시다!! 전체 포스트는 “Numerical Analysis“에서 확인할 수 있습니다.

Fixed Point Iteration

FPI 방식은 비선형 방정식 $f(x) = 0$의 근을 찾기 위한 수치적 방법 입니다.

함수 $f(x)$에 대해 $f(r) = 0$를 만족하는 $r$을 찾기 위해 $f(x) = x - g(x)$로 표현하고, $r = g(r)$을 만족하는 $r$을 찾도록 합니다. 그리고 아래의 점화식을 이용해 $r$을 찾을 수 있습니다.

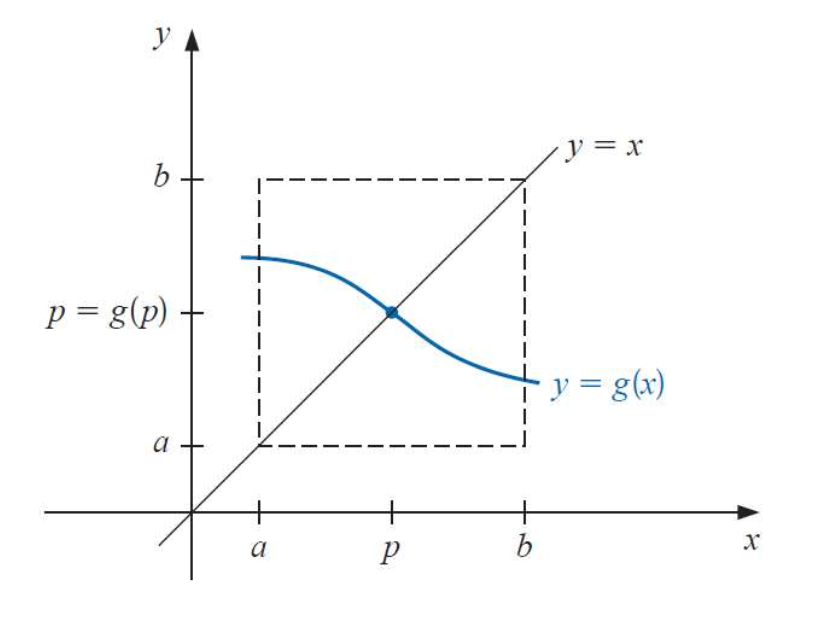
1. 초기값 $p_0$가 있습니다.
2. $p_{n+1} = g(p_n)$ 점화식을 수행합니다.

Convergence

Lipchitz Continuity

함수 $f(x)$가 어떤 구간에서 아래의 조건을 만족한다면,

\[\|f(x) - f(y) \| \le L \| x - y \|\]

이 함수를 “Lipschitz Continuous”라고 합니다. 그리고 $L$을 “Lipschitz constant”라고 합니다.

조건을 좀더 쉽게 표현하면, 도함수 $f’(x)$의 크기가 Bounded인 상황이라고 볼 수 있습니다. 그러면, 함수 그래프의 기울기가 너무 가파르게 변화하거나 폭발하지 않는다는 것을 말합니다.

\[\| f'(x) \| \le L\]

Contraction Mapping

함수가 Lipschitz Continuity를 만족하고 $L < 1$라면, 이 함수가 “수축 사상(Contraction Mapping)”을 만족한다고 합니다. 이것은 두 점 사이의 거리 $| x - y|$가 함수 매핑에 의해 $| f(x) - f(y) |$로 저 가까워짐을 말합니다.

\[\|f(x) - f(y) \| < \| x - y \|\]

예시를 들자면, $f(x) = x/2$와 같은 함수가 될 수 있습니다.

수축 사상은 “모든 점들은 점점 더 가까이 움직이게 만드는 함수”입니다. 이것은 수축의 본질이고, 이번 포스트에서 다룰 “Fixed-point Iteration”의 핵심이라고 할 수 있습니다.

Locally Convergence

FPI 방식에서 사용하는 $g(x)$에 아무 조건도 걸려 있지 않다면, 점화식으로 솔루션 $r$를 찾을 수 있음을 보장하지 않습니다. (해를 찾을 수도 있고, 못 찾을 수도 있다는 말입니다.)

그런데, 함수 $g(x)$가 구간 $[a, b]$ 내에서 “수축 사상($| g’(x) | < 1$)”을 만족한다면, 이 구간에서 수렴을 기대할 수 있습니다. 단, 수렴을 보장하지는 않습니다.

수렴하는 고정점은 $[a, b]$ 구간내에 존재한다고 기대 되지만, FPI으로 그 고정점에 반드시 수렴한다는 걸 보장하지 않습니다.

그 고정점에 수렴하기 위해선, 초기값 $p_0$가 고정점 $r$에 충분히 가까워야 선형 수렴이 보장 됩니다.

“충분히 가까워야 한다”니 뭔가 표현이 찜찜-합니다;; 구간 $[a, b]$ 내의 일부의 초기값에 대해서만 수렴한다는 말이고, 그래서 이걸 “국소 수렴”이라고 표현합니다.

Global Convergence (Fixed-Point Theorem)

만약 구간 $[a, b]$ 내에서 어떤 초기값을 잡더라도 항상 고정점으로 수렴하고 싶다면 추가 조건이 필요 합니다!

만약 함수 $g(x)$가 “자기 사상(self-mapping)”을 만족한다면 FPI는 전역 수렴을 보장 합니다.

For any $x \in [a, b]$,

\[g(x) \in [a, b]\]

이제 이 두 조건을 정리해 다시 기술해보겠습니다. 이것을 고정점 정리라고 합니다.

Let $g \in C[a, b]$ be s.t. $g(x) \in [a, b]$ for all $x$ in $[a, b]$. (self-mapping)

Supp. that $g’$ exists on $(a, b)$ and there is a constant $0 < K < 1$ s.t. for all $x \in (a, b)$, $| g’(x) | \le K$. (contraction mapping)

Then for any number $p_0$ in $[a, b]$, the sequence defined by $p_n = g(p_{n-1})$ for $n \ge 1$,
converges to the unique fixed point $r$ in $[a, b]$.

저번 학기에 들었던 “상미분방정식(MATH412)” 과목이 생각나는 정리 입니다. 그때, “바나흐 고정점 정리(Banach Fixed-point Theorem)”에 대해 배웠는데요. 그때는 정리가 임의의 “완비 거리 공간 $X$”를 대상으로 했다면, 여기에서는 유계의 닫힌 실수 구간 $[a, b]$에 대해서 얘기 합니다.

상미분방정식을 듣던 당시에는 수업에서 오랜만의 수학과 수업에 정신을 아예 못차렸는데, 만약 “수치해석개론”을 미리 들었더라면, 좀더 쉽게 이해하고 수업을 따라갔을 것 같네요 😅

Error Bound

Fixed-point Iteration이 위의 고정점 정리를 만족하는 상황이라면, 이 근사법에 대한 오차 경계를 유도할 수 있습니다. 이때, 2가지 오차 경계를 유도할 수 있습니다.

Error Bound - 1

If $g$ satisfies the “Fixed-point Theorem”, then bounds for the error involved in suing $p_n$ to approximate the fixed point $r$ are given by

\[\| p_n - r \| \le K^n \max \left\{ p_0 - a, b - p_0 \right\}\]

TODO: 증명

Error Bound - 2

If $g$ satisfies the “Fixed-point Theorem”, then bounds for the error involved in suing $p_n$ to approximate the fixed point $r$ are given by

\[\| p_n - r \| \le \frac{K^n}{1-K} \| p_1 - p_0 \|\]

TODO: 증명

둘 중 어떤 것을 쓰는게 좋을까?

TODO

맺음말

먼저 살펴본 “/2025/03/12/bisection-method/”는 이분 탐색의 컨셉으로 근을 찾는 방식 입니다. “Fixed-point Iteration”은 고정점(fixed-point)을 찾기 위한 재귀적인 방법이라고 할 수 있습니다. 이때, 재귀적인 방법이 발산하지 않고 수렴하기 위해서는 함수가 자기 사상(self-mapping)라는 성질이 필요한 것이구요!