Method of False Position

수학과 복수전공을 위해 졸업 마지막 학기에 “수치해석개론” 수업을 듣게 되었습니다. 수학과 졸업시험도 겸사겸사 준비할 겸 화이팅 해봅시다!! 전체 포스트는 “Numerical Analysis“에서 확인할 수 있습니다.

Improved Bisection Method

근을 찾는 방법으로 제일 먼저 배웠던 “이분법(Bisection Method)“를 기억 하는가요?

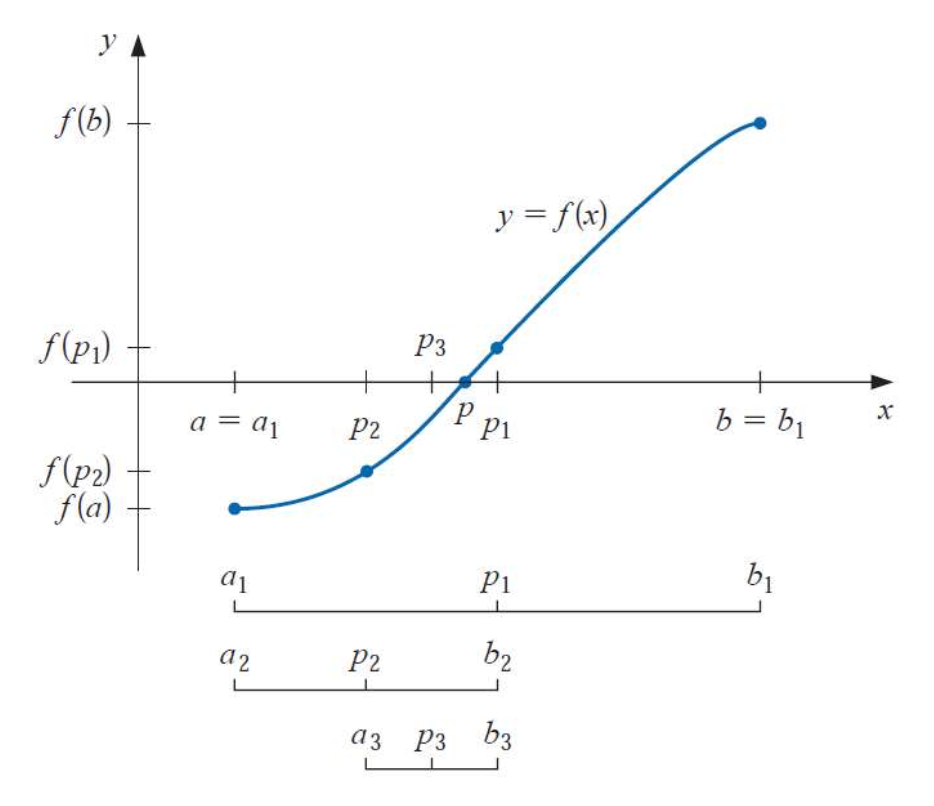
이 방식은 부호를 고려하여, 가운데점을 새로운 끝점으로 업데이트 했습니다.

그러나 1차 수렴 속도를 가지고 있어, 느리다는 단점이 있었고 이걸 개선하기 위해 “고정점 방법”, “뉴턴법”을 살펴보았습니다.

이번 포스트에서는 이분법의 컨셉을 그대로 사용하면서, 개선한 방법인 “Method of False Position” 방법을 살펴봅니다!

Method of False Position

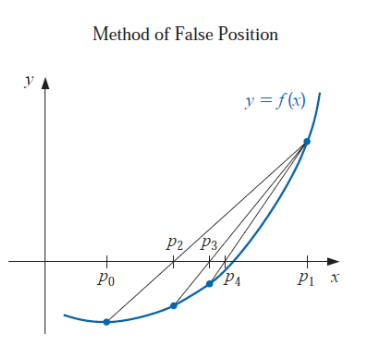
한국에서는 “가위치기” 기법라고 부르기도 하는데요. 이 기법은 이분법에서 다음 지점을 정할 때, 단순히 가운데 지점 $p_{n+2} = \frac{p_n + p_{n+1}}{2}$이 아니라 아래의 조건을 만족하는 지점을 고릅니다.

\[p_{n+2} = p_{n+1} - \frac{f(p_{n+1})}{f'(p_{n+1})}\]

그런데, 일반적으로 $f’(p_{n+1})$를 구하기 어렵기 때문에, 아래와 같이 미분값의 근사값을 사용합니다.

\[p_{n+2} = p_{n+1} - f(p_{n+1}) \cdot \frac{p_{n+1} - p_n}{f(p_{n+1} - f(p_n))}\]

그리고 $f(p_{n+1}) \cdot f(p_{n+2})$의 부호를 판단하여, 양끝 점을 업데이트 합니다.

• $f(p_{n+1}) \cdot f(p_{n+2}) < 0$
  • $[p_n, p_{n+1}] \rightarrow [p_{n+1}, p_{n+2}]$
• $f(p_{n+1}) \cdot f(p_{n+2}) > 0$
  • $[p_n, p_{n+1}] \rightarrow [p_n, p_{n+2}]$

vs Secant Method

사실 이 방식은 “할선법(Secant Method)“에서 $f(a) f(b) < 0$ 조건이 추가된 것 입니다. 할선법은 이 조건 없이 일반적으로 상황에서 근을 찾습니다.

\[x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} \approx x_n - f(x_n) \cdot \frac{x_n - x_{n-1}}{f(x_n) - f(x_{n-1})}\]

할선법은 $f(x) = 0$인 근을 반드시 찾는다고 보장하지 않습니다. 그러나, Method of False Position은 근을 찾을 수 있다는게 보장 됩니다.

맺음말

이것으로 “근 찾기(Root Finding)” 챕터를 모두 살펴보았습니다. 이어지는 포스트에선 함수를 근사하는 방법인 “보간(Interpolation)”에 대해 살펴봅니다. 화이팅!