Secant Method
수학과 복수전공을 위해 졸업 마지막 학기에 “수치해석개론” 수업을 듣게 되었습니다. 수학과 졸업시험도 겸사겸사 준비할 겸 화이팅 해봅시다!! 전체 포스트는 “Numerical Analysis“에서 확인할 수 있습니다.
Newton’s Method
지난 포스트에서 살펴본 “Newton’s Method“는 방정식의 근을 찾기 위한 방법이고, 이차 수렴 하는 방식 입니다.
\[p_{n+1} = p_n - \frac{f(p_n)}{f'(p_n)}\]하지만, 도함수 $f’(x)$를 정확히 알고 있어야 하기에 미분 계산이 어려운 경우는 사용하기 어려웠습니다. 이것을 보완한 방식이 “Secant Method” 입니다.
Secant Method
도함수 $f’(x)$를 직접 구하는 것이 아니라 아래와 같이 근사 합니다.
\[f'(x) \approx \frac{f(x_n) - f(x_{n-1})}{x_n - x_{n-1}}\]이제 “Secant Method”에 따라 공식을 다시 작성하면 아래와 같습니다.
\[x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} \approx x_n - f(x_n) \cdot \frac{x_n - x_{n-1}}{f(x_n) - f(x_{n-1})}\]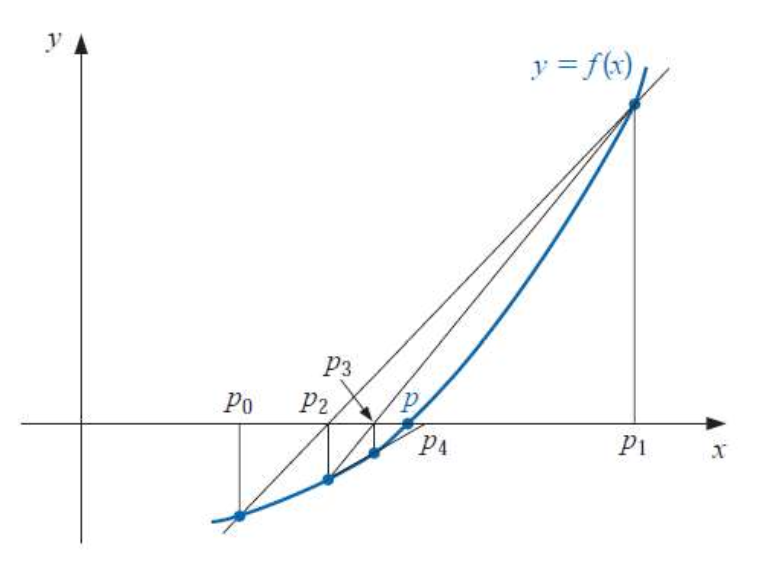
Convergence
이차 수렴의 속도를 갖는 뉴턴 방법 보다는 수렴 속도가 느려집니다.
맺음말
이어서 할선법과 이분법을 결합한 방법인 “Method of False Position”에 대해 살펴봅니다!
