Lagrange Interpolation

수학과 복수전공을 위해 졸업 마지막 학기에 “수치해석개론” 수업을 듣게 되었습니다. 수학과 졸업시험도 겸사겸사 준비할 겸 화이팅 해봅시다!! 전체 포스트는 “Numerical Analysis“에서 확인할 수 있습니다.

주어진 데이터의 점들을 정확히 통과하는 다항식을 찾는 방법 입니다. 라그랑주 다항식(Lagrange Polynomial)을 사용해 데이터를 보간(interpolation) 하는 기법 입니다. 다른 보간법으로는 뉴턴의 보간법이 있습니다.

Linear Interpolation

2차원의 두 점 $p_0 = (2, 4)$와 $p_1 = (5, 1)$이 있을 때, 둘을 잇는 직선의 방정식을 고안해봅시다. 그러면,

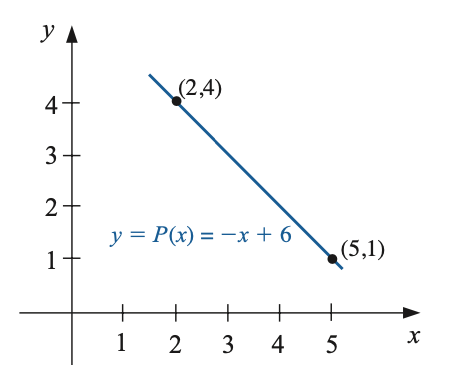
이런 일차 방정식이 됩니다. 라그랑지 보간법은 동일하게 이 식을 유도하지만, 컨셉이 다릅니다. 라그랑지 보간법에서 기저 다항식은 아래와 같습니다.

\[\begin{aligned} L_0(x) &= \frac{x-5}{2-5} \\ L_1(x) &= \frac{x-2}{5-2} \end{aligned}\]

이 기저 다항식은 특별한 성질을 가지고 있는데요. $p_0$에서는 1인 값을 가지고, 다른 모든 점에서는 0인 값을 갖습니다. 이건 마치 “스포트라이트” 같은 역할을 합니다. $p_0$에서 빛나고, 다른 곳에서는 꺼집니다.

기저 다항식 들을 모아서 아래와 같이 구성 합니다.

\[P(x) = y_0 \cdot L_0(x_0) + y_1 \cdot L_1(x_1)\]

이렇게 전체식을 구성하면, 다항식의 값이 그 점 $p_i$에서 그 점 $y_i$ 값을 갖고 통과하게 됩니다.

Lagrange Interpolation

위의 아이디어를 확장한 것이 “라그랑주 보간법” 입니다. 라그랑주 다항식 $L_i(x)$는 아래와 같이 정의 합니다.

\[L_i (x) = \prod_{j=1, j \ne i} \frac{x-x_j}{x_i - x_j}\]

그리고 라그랑주의 보간점은 아래와 같은 보간 다항식 $P(x)$으로 정의 합니다.

For given $n+1$ data pints: $(x_0, y_0), (x_1, y_1), …, (x_n, y_n)$,

\[P(x) = \sum_{i=0}^n y_i L_i (x)\]

Property

Interpolating Constant Function

$f(x) = 1$인 상수 함수를 라그랑주 보간법으로 표현한다고 해봅시다.

\[P(x) = \sum_i f(x_i) \cdot L_i(x) = 1\]

그런데, $f(x) = 1$이기 $f(x_i) = 1$이 됩니다. 따라서

\[P(x) = \sum_i 1 \cdot L_i(x) = 1\]

즉, $\sum L_i = 1$를 만족 합니다!

Degree of Lagrange Interpolation

라그랑주 다항식 $L_i(x)$는 $n-1$차 다항식 입니다. 그런데, 이것들의 선형 결합인 $P(x) = \sum y_i L_i(x)$의 차수는 $n-1$ 보다 낮아질 수 있습니다.

바로 직관적인 예시가 바로 위에서 살펴본 상수 함수에 대한 보간 함수 입니다. $n-1$차 다항식을 조합하여 0차 다항식을 $P(x)$를 유도 하였습니다.

이 이야기는 뒤에 나올 “라그랑주 다항식이 다항 공간의 기저를 이룬다”와 이어 집니다.

Degree of Lagrange Polynomial

정상적인 상항에서 라그랑주 다항식 $L_i(x)$의 차수는 $n-1$로 고정 입니다. 그러나, 입력된 점이 $x$ 값이 동일한 “중복 노드”를 가지고 있다면, $L_i(x)$의 차수가 $n-1$보다 줄어듭니다.

라그랑주 다항식은 아래와 같이 정의 됩니다.

\[L_i (x) = \prod_{j=1, j \ne i} \frac{x-x_j}{x_i - x_j}\]

그런데 만약 $j \ne i$ 중에서 $x_j = x_i$인 노드가 있다면, $\frac{x_i - x_j}{x_i - x_j}$인 부분이 소거 됩니다. 또는 분모가 0이 되어 정의되지 않는다고 볼 수도 있습니다. 이 논의에서는 분모가 0이 되지 않고 소거 된다고 설정 합니다.

이런 데이터의 $x$ 값이 같은 경우가 발생할 때마다, $L_i(x)$의 차수가 낮아집니다.

Lagrange Polynomials forms Polynomial Basis

$\left\{ L_i(x) \right\}$ is the basis of $\mathbb{P}_{n-1}$.

$\mathbb{P}_{n-1}$은 최고차항이 $n-1$ 이하인 다항식들의 공간 입니다. 이 공간의 차원은 $n$ 입니다. (상수(0차) 다항식과 $1$부터 $n-1$차 다항식을 포함하기 때문입니다.)

$\left\{L_i(x)\right\}$는 $n$개 함수로 구성된 집합입니다. 각각은 $\deg \le n-1$ 입니다.

$\left\{L_i(x)\right\}$가 기저를 이루기 위해서는 각각이 “선형 독립”임을 보여야 합니다. 이것은 아래의 조건에 의해 보장 됩니다.

\[L_i(x_j) = \begin{cases} 1 & i = j \\ 0 & i \ne j \end{cases}\]

선형 독립이고, $n$개이므로, $\mathbb{P}_{n-1}$의 기저가 됩니다.

Interpolation Operator

함수 $f(x)$를 $n$개의 점 $(x_1, f(x_1)), \dots, (x_n, f(x_n))$에 Interpolation한 함수를 일반적으로 아래와 같이 표기 합니다.

\[I_n f\]

그리고 $I_n f \approx f$로 근사된다고 표현 합니다. 보간한 함수를 $P(x)$가 아니라 $I_n f$로 표현하는 이유는 표기에서 “몇 개 점으로, 어떤 함수를 보간한 것인지” 알 수 있기 때문입니다.

예를 들어, $f(x) = \sin x$라고 한다면, 표기는 $I_n(\sin x)$로 할 수 있습니다. 이것은 $\sin x$ 함수를 $n$개 점에서 보간한 함수임을 말합니다.

$I_n$을 일종의 “Interpolation Operator”라고 볼 수 있습니다. 표기를 확장하면 아래와 같이 보간 방법을 구분해 표기할 수도 있습니다.

• $I_n^{\text{lag}}$
  • 라그랑주 보간
• $I_n^{\text{newt}}$
  • 뉴턴 보간

Theorem

Let $(x_1, y_1), \dots, (x_n, y_n)$ be $n$ points with distinct $x_i$.
Then there exists a unique polynomial $P \in \mathbb{P}_{n-1}$ s.t. $P(x_i) = y_i$ for $i=1,\dots,n$.

주어진 $n$개 점을 지나도록 하는 다항식이 유일하게 존재한다고 말하는 정리 입니다. 참고로 보간법의 재료에 초월 함수까지 허용한다면, 보간 함수가 유일하지 않을 수 있습니다. 초월 함수는 훨씬 더 “풍부한” 함수 공간이기 때문입니다.

Existence

라그랑지 보간법이 이 정리의 존재성을 증명 합니다.

Uniqueness

유일성에 대한 증명을 위해, 귀류법을 사용합니다. 또다른 보간 다항식 $Q(x)$가 있다고 가정 합니다. 이것은 $Q(x_i) = y_i$를 만족하지만, $Q(x) \ne P(x)$ 입니다.

두 다항식의 차이를 계산하는 $R(x) = P(x) - Q(x)$를 생각해봅시다. 그러면, $R(x)$도 여전히 $R(x) \in \mathbb{P}_{n-1}$ 입니다.

그런데, $R(x_i)$는 그 정의에 따라 $R(x_i) = 0$을 만족 합니다. 즉, $R(x)$는 $n$개의 서로 다른 근을 갖습니다.

“대수의 기본 정리(Fundamental Theorem of Algebra)”에 따르면, $n-1$차 이하의 다항식은 최대 $n-1$개의 서로 다른 근만 가질 수 있습니다. 그런데, $R(x)$는 $n$개의 근을 가지니까, $\deg(R) \ge n$이 됩니다. 그런데, 앞에서 $R(x) \in \mathbb{P}_{n-1}$라고 했으니 모순이 발생 합니다.

모순이 발생 했으니, 처음에 가정한 $Q(x) \ne P(x)$ 가정이 틀렸습니다. 따라서, $Q(x) = P(x)$이고 보간 다항식은 유일 합니다.