Lotteries & Lottery Preference

졸업을 위해 마지막 학기에 “미시경제학” 수업을 듣게 되었습니다. 경제학원론 수업을 재밌게 들어서 경제 쪽이랑 궁합이 좋은 줄 알고 신청 했는데, 웬걸… 이 과목은 사실상 수학과 과목 이었습니다.. ㅋㅋ 그래도 수학과 복수전공도 하고 있으니, 이 수업도 힘내서 잘 들어봅시다! 전체 포스트는 “미시경제학” 카테고리에서 확인하실 수 있습니다.

Lotteries

지금까지 살펴본 선호(Preference), 효용 함수(Utility Functions), 선택 함수(Choice Functions) 모두 선택과 결과가 고정적으로 정해지는 상황이었습니다.

“복권(Lotteries)”는 확률적인 결과를 포함하는 상품 입니다. 선택을 하면, 보상이 확률적으로 결정 됩니다.

어떤 보상의 집합을 $Z$라고 할 때, Lottery $p$는 $z \in Z$에 확률 $p(z)$를 할당 합니다.

로터리에서 확률이 0보다 큰 보상의 집합을 support $\text{supp}(p)$라고 합니다.

\[\text{supp}(p) = \left\{ z \in Z | p(x) > 0 \right\}\]

• $L(Z)$
  • set of all lotteries over $Z$
• $[z]$
  • the lottery that yields the prize $z$ with probability 1
  • Deterministic Lottery, Unity Lottery

그리고 복권 “Lottery”에 대한 표기는 아래와 같이 할 수 있습니다.

each $\alpha_k = p(z_k)$

\[p = \alpha_1 \cdot z_1 \oplus \cdots \oplus \alpha_n \cdot z_n\]

Visualize set of lotteries

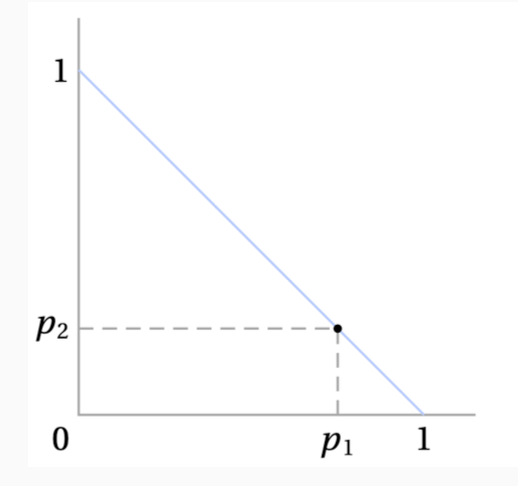
$Z$가 두 개의 상품 $z_1, z_2$로 구성 되어 있고, 각 상품에 대한 확률이 $p_1, p_2$라고 합시다.

확률의 합은 항상 1이어야 하기 때문에 $p_1 + p_2 = 1$을 만족하고, 이는 위의 그림처럼 평면 위에 표현할 수 있습니다.

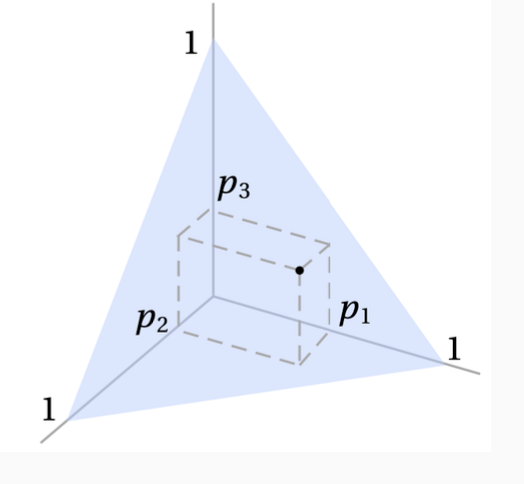
만약, $Z$가 3개의 상품으로 구성 되어 있었다면, 비슷하게 3차원의 공간 뒤에 그릴 수 있습니다.

2차원의 직선과, 3차원의 면은 모두 2개 상품, 3개 상품에서 만들 수 있는 모든 복권의 집합을 표현한 것 입니다.

Preference over Lotteries

어떤 사람 앞에 여러 종류의 복권이 있습니다. 사람마다 선호하는 복권이 다를 테죠. 사람들이 어떤 복권을 선호 하는지에 대해 얘기해봅니다.

Pessimist

비관주의자의 예시 입니다. 이 사람은 복권을 평가할 때, 그 안에서 일어날 수 있는 결과들 중 “가장 나쁜 결과”를 기준으로 판단 합니다.

그 나쁜 결과가 아무리 작은 확률을 갖더라도, 비관주의자는 가장 나쁜 결과를 기준으로 그 복권을 평가 합니다.

비관주의자는 각 복권을 가장 나쁜 결과 $w(p)$로 대체해서 생각 합니다. 그리고, 그 나쁜 결과 중에서 가장 큰 효용을 가지는 복권을 선호 합니다.

Good and Bad

이 사람은 복권은 좋은것(good)과 나쁜것(bad) 두 집단으로 분할 하여 생각 합니다.

그리고, 좋은것의 확률 모두 더해 $G(p)$로 둡니다.

\[G(p) = \sum_{z\in\text{good}} p(z)\]

이 사람은 각 복권에서 확률 $G(p)$를 구하고, 이것이 높은 복권을 선호 합니다.

이 사람은 좋은 결과의 가치는 무시하고, 좋은 결과가 나올 확률만을 기준으로 선택 합니다.

Minimizing Options

이 사람은 일어날 수 있는 경우의 수가 작은 걸 선호 합니다. 이유를 들어보니, 가능한 경우의 수가 적을수록 대비하기 쉽고 안심 된다고 하네요. 즉, 불확실성이 적을수록 선호하는 사람 입니다.

\[p > q \iff \| \text{supp}(p) \| \ge \| \text{supp}(p) \|\]

이런 경우는 어떤 상황을 준비하는게 중요한 상황, 예를 들면 의료 수술이나 군사 작전에선 이 선호가 유용할 수 있습니다.

Summary

위에서 복권에 대한 3가지의 선호 방식을 살펴보았습니다…만 복권에 대한 선호는 정말 다양하게 정의할 수 있습니다.

앞으로는 이런 복권 선호들 중에서 “좋은 성질”을 만족하는 특별한 복권 선호들만 골라서 좀더 살펴보고자 합니다.

Properties

“복권 선호”에서 정의할 수 있는 여러 성질들에 대해 살펴봅니다.

Continuity

상품권 100만원, 70만원, 40만원이 있습니다. 만약 100만원이 0.5 확률, 40만원이 0.5 확률인 복권이 있다면, 그 사람은 70만원과 그 복권을 무차별하게 선호 한다고 합니다.

위와 같은 상황이 복권에 대한 선호가 Continuity를 만족한다고 합니다. 형식을 갖춰서 적어보면,

복권에 대한 보상 $Z$에 대해 아래와 같이 연속적인 선호가 있습니다.

\[[a] \succ [b] \succ [c]\]

그리고, $b$와 동등한 가치로 여겨지는 어떤 복권을 만들어낼 수 있다면,

\[[b] \sim \alpha \cdot a \oplus (1-\alpha) \cdot c\]

“선호 관계가 복권에 대해 연속성을 갖는다”고 말합니다.

비관주의자가 갖는 선호는 연속성을 갖지 못합니다. 왜냐하면, 비관주의자는 $a$와 $c$를 섞은 복권이 있으면 항상 안 좋은 선택지 $c$를 기준으로 판단하기 때문입니다.

“Good and Bad” 선호는 vacuously 연속이라고 합니다. 그 이유는 좋은 결과가 나올 확률의 총합 $G(p)$만 보고 판단하기 때문에 보상에 대한 조합이 의미가 없기 때문입니다. 이 선호에서는 연속성을 테스트할 상황 자체가 없다고 합니다.

“Minimizing Options”도 vacuously 연속이라고 합니다. 왜냐하면, $[a] \succ [b] \succ [c]$와 같은 보상 간의 선호가 아예 정의되지 않기 때문입니다. 그래서 애초에 연속성에 대한 전재가 성립하지 않고, 연속성이 vacuously 만족한다고 봅니다.

* “vacuously 연속한다”는 것은 공허하게 연속이라고 표현하는데, 조건을 만족해야 할 상황 자체가 아예 존재하지 않기 떄문에 조건을 자동으로 만족한다는 것을 말합니다.

Compound Lottery

복합 복권, 복권 안의 복권. 두 단계 이상의 무작위성이 있을 때를 모델링 하는 방법 입니다.

보상에 대한 집합 $Z$가 있고, 그 위에 정의된 복권 $p_1, …, p_k$가 있습니다. 이들은 $L(Z)$의 원소 입니다.

복합 복권은 아래와 같이 정의 됩니다.

\[\alpha_1 p_1 \oplus \alpha_2 p_2 \oplus \cdots \oplus \alpha_k p_k\]

이것을 각 재화 $z \in Z$에 대한 확률을 풀어쓰면 이렇게 됩니다.

\[\text{Prob}(z) = \sum_{i=1}^{k} \alpha_k \cdot p_k(z)\]

Independence

복권에서 특정 항목을 더 선호되는 다른 걸(상품 or 복권)로 바꾼다면, 이전 복권과 신규 복권 사이의 복권 선호는 대체한 상품 사이의 선호 관계를 그대로 따른다. 즉, 대체된 상품만 보면 되고, 대체되지 않은 다른 상품들은 신경 쓰지 않아도 된디. 각 상품들은 서로 영향을 주지 않는 “독립성”을 갖는다.

수식으로 이해하는게 좀더 편합니다.

두 “상품” 사이에 아래와 같은 선호가 성립 합니다.

\[[a] \succcurlyeq [z_k]\]

복권 선호가 독립성을 갖는다면, 신규 복권과 기존 복권은 대체된 상품이 갖는 선호를 그대로 따릅니다.

\[\begin{gather*} \cdots \oplus \alpha_k \cdot {\color{red} a} \oplus \cdots \\ \succcurlyeq \\ \cdots \oplus \alpha_k \cdot {\color{red} z_k} \oplus \cdots \end{gather*}\]

그리고 이 명제에 대한 역도 성립 합니다.

두 “복권” 사이에 아래와 같은 선호가 성립 합니다.

\[\beta \cdot a \oplus (1-\beta) \cdot b \succcurlyeq [z_k]\]

복권 선호가 독립성을 갖는다면, 신규 복권과 기존 복권은 대체된 복권이 갖는 선호를 그대로 따릅니다.

\[\begin{gather*} \cdots \oplus \alpha_k \cdot {\color{red} (\beta \cdot a \oplus (1-\beta) \cdot b)} \oplus \cdots \\ \succcurlyeq \\ \cdots \oplus \alpha_k \cdot {\color{red} z_k} \oplus \cdots \end{gather*}\]

그리고 이 명제에 대한 역도 성립 합니다.

Monotonicity

“단조성”은 상품의 선호 체계와 복권에 대한 선호 체계가 일관성 있도록 하는 성질 입니다.

두 상품 $a$, $b$가 있을 때, 두 상품 사이에는 $a \succ b$의 선호가 존재합니다. 두 상품으로 만들 수 있는 복권 집합 $L(Z)$에 대해서 사람들의 복권에 대한 선호는 $a$ 상품이 당첨될 확률 $\alpha$가 높을수록 선호 됩니다.

합리적인 선택을 하기 위해선, 더 선호되는 상품인 $a$가 나올 확률이 높아질 수록 그 복권을 더 선호해야 합니다. 만약 그걸 좋아하지 않는다면 비합리적인 선택을 한다는 것이죠. 복권의 “단조성”은 선호 체계가 일관성 있게 구성되는 증거로 사용 합니다.

Independence implies Monotonicity

Let $Z$ be a set of prizes.

Assume that $\succcurlyeq$, a preference relation over $L(Z)$, satisfies the independence property.

Let $a$ and $b$ be two prizes with $[a] \succ [b]$, and let $\alpha$ and $\beta$ be two probabilities. Then

\[\begin{gather*} \alpha > \beta \\ \iff \\ {\color{red} \alpha} \cdot a \oplus (1 - \alpha) \cdot b \succ {\color{red} \beta} \cdot a \oplus (1 - \beta) \cdot b \end{gather*}\]

복권 $p_{\alpha}$를

\[p_{\alpha} = \alpha \cdot a \oplus (1 - \alpha) \cdot b\]

라고 합시다. 복권에 대한 선호 관계가 독립성을 만족하므로, 복권 $p_{\alpha}$에서 $a$를 $b$로 대체한 복권에 대해 아래의 선호가 성립 합니다.

\[p_{\alpha} \succ \alpha \cdot b \oplus (1 - \alpha) \cdot b\]

위의 선호 관계는 사실 아래의 같습니다.

\[p_{\alpha} \succ [b]\]

여기에서 잠깐 $p_{\alpha}$를 아래와 같이 바꿔서 표현 합니다.

\[p_{\alpha} = (\beta/\alpha) \cdot p_{\alpha} \oplus (1 - \beta/\alpha) \cdot p_{\alpha}\]

위의 표현은 깊게 생각할 건 없고, 단순히 $p_{\alpha}$를 $\beta / \alpha$의 확률로 분할한 것 입니다. 일종의 수식 전개의 트릭이라고 생각합시다!

다시 선호의 독립성을 사용해 이런 선호 관계를 얻을 수 있습니다.

\[\begin{aligned} p_{\alpha} &= (\beta/\alpha) \cdot p_{\alpha} \oplus (1 - \beta/\alpha) \cdot {\color{red} p_{\alpha}} \\ &\succ (\beta/\alpha) \cdot p_{\alpha} \oplus (1 - \beta/\alpha) \cdot {\color{red} b} \end{aligned}\]

이제 마지막에 얻은 복권에 대한 식을 잘 정리하면

\[\begin{aligned} &(\beta/\alpha) \cdot p_{\alpha} \oplus (1 - \beta/\alpha) \cdot b \\ &= \beta \cdot a \oplus (1 - \beta) \cdot b \end{aligned}\]

따라서,

\[{\color{red} \alpha} \cdot a \oplus (1 - \alpha) \cdot b \succ {\color{red} \beta} \cdot a \oplus (1 - \beta) \cdot b\]

$\blacksquare$

맺음말

이어지는 포스트에서는 “기대 효용(Expected Utility)“에 대해 살펴봅니다.

경제학적 선택을 할 때, 많은 것들이 불확실성을 가지고 있습니다. 이번에 살펴본 복권(Lotteries)는 이 불확실을 모델링한 것 입니다. 기대 효용은 불확실함이 있을 때, 사람들의 선택의 기준이 됩니다. 그리고 사람들이 기대 효용에 따라 행동한다는 것을 전제로 경제학 이론이 발전하게 됩니다.