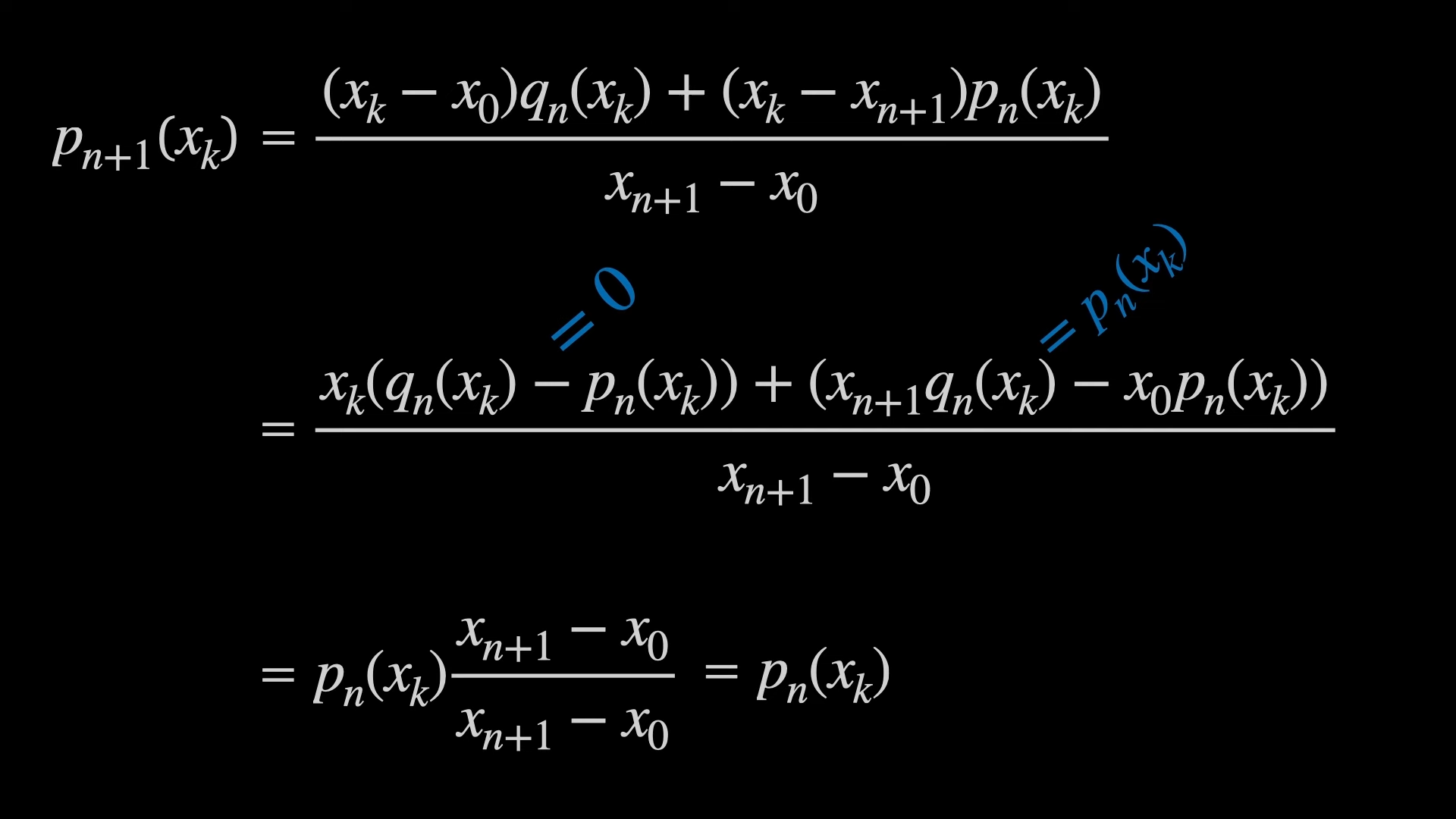Newton’s Divided Differences

수학과 복수전공을 위해 졸업 마지막 학기에 “수치해석개론” 수업을 듣게 되었습니다. 수학과 졸업시험도 겸사겸사 준비할 겸 화이팅 해봅시다!! 전체 포스트는 “Numerical Analysis“에서 확인할 수 있습니다.

Divided Differences

뉴턴의 방법을 알기 전에 기본 재료가 되는 “나눗셈 차분(Divided Difference)”을 먼저 알아야 합니다. 주어진 여러 점들을 이용해서 함수의 변화 양상을 계산하는 방법 입니다.

\[c_0 = f[x_0] = f(x_0)\]

• 0차 나눗셈 차분
  • 말 그대로 함수의 값 입니다.
  • 계수 $c_0$에 해당

\[c_1 = f[x_0, x_1] = \frac{f(x_1) - f(x_0)}{x_1 - x_0}\]

• 1차 나눗셈 차분
  • 두 점 사이의 기울기(평균 변화율) 입니다.

\[c_2 = f[x_0, x_1, x_2] = \frac{f[x_1, x_2] - f[x_0, x_1]}{x_2 - x_0}\]

• 2차 나눗셈 차분
  • 기울기의 변화율 입니다.
  • 두 1차 나눗셈 차분의 값으로 계산한 나눗셈 차분 입니다.

\[c_i= f[x_0, \cdots, x_i] = \frac{f[x_1, \cdots, x_i] - f[x_0, \cdots, x_{i-1}]}{x_i - x_0}\]

• $i$차 나눗셈 차분
  • 두 $(i-1)$차 나눗셈 차분의 값으로 계산한 나눗셈 차분 입니다.

0부터 $i$차 나눗셈 차분을 살펴보면, 그 정의에 모두 하위 차분의 값을 필요로 합니다. 즉, 재귀적(Recursive)으로 나눗셈 차분의 값을 계산하게 됩니다.

Newton’s Divided Difference

뉴턴은 위에서 정의한 나눗셈 차분으로 $n$개 점을 보간하는 방법을 고안합니다. 방법은 아래와 같습니다.

\[\begin{aligned} I_n f(x) = f[x_1] &+ f[x_1, x_2](x-x_1) \\ &+ f[x_1, x_2, x_3](x-x_1)(x-x_2) \\ &+ \cdots \\ &+ f[x_1, \dots, x_n] \prod_{i=1}^{n} (x - x_i) \end{aligned}\]

나눗셈 차분 부분만 계수 $c_k$로 표현하면 아래와 같습니다.

\[\begin{aligned} I_n f(x) &= c_0 + c_1(x-x_1) + c_2(x-x_1)(x-x_2) + \cdots + c_{n-1} \prod_{i=0}^{n-1} (x - x_i) \\ \text{where} \quad c_k &= f[x_1, \dots, x_k] \end{aligned}\]

The divided difference table

‘Dr. Will Wood’의 영상에서는 나눗셈 차분을 쉽게 계산하기 위한 테이블을 제시 합니다.

Dr. Will Wood

손으로 나눗셈 차분을 구해야 한다면, 이렇게 테이블을 만들어서 계산하는게 실수하지 않는 방법일 것 같습니다. 그리고 나눗셈 차분이 재귀에 의해 유도된다는 것도 시각적으로 확인할 수 있습니다.

Dr. Will Wood

각 단계의 나눗셈 차분을 모두 계산했다면, 나눗셈 차분의 맨 윗 부분들만 모아서 최종 형태를 유도할 수 있습니다.

How interpolation works

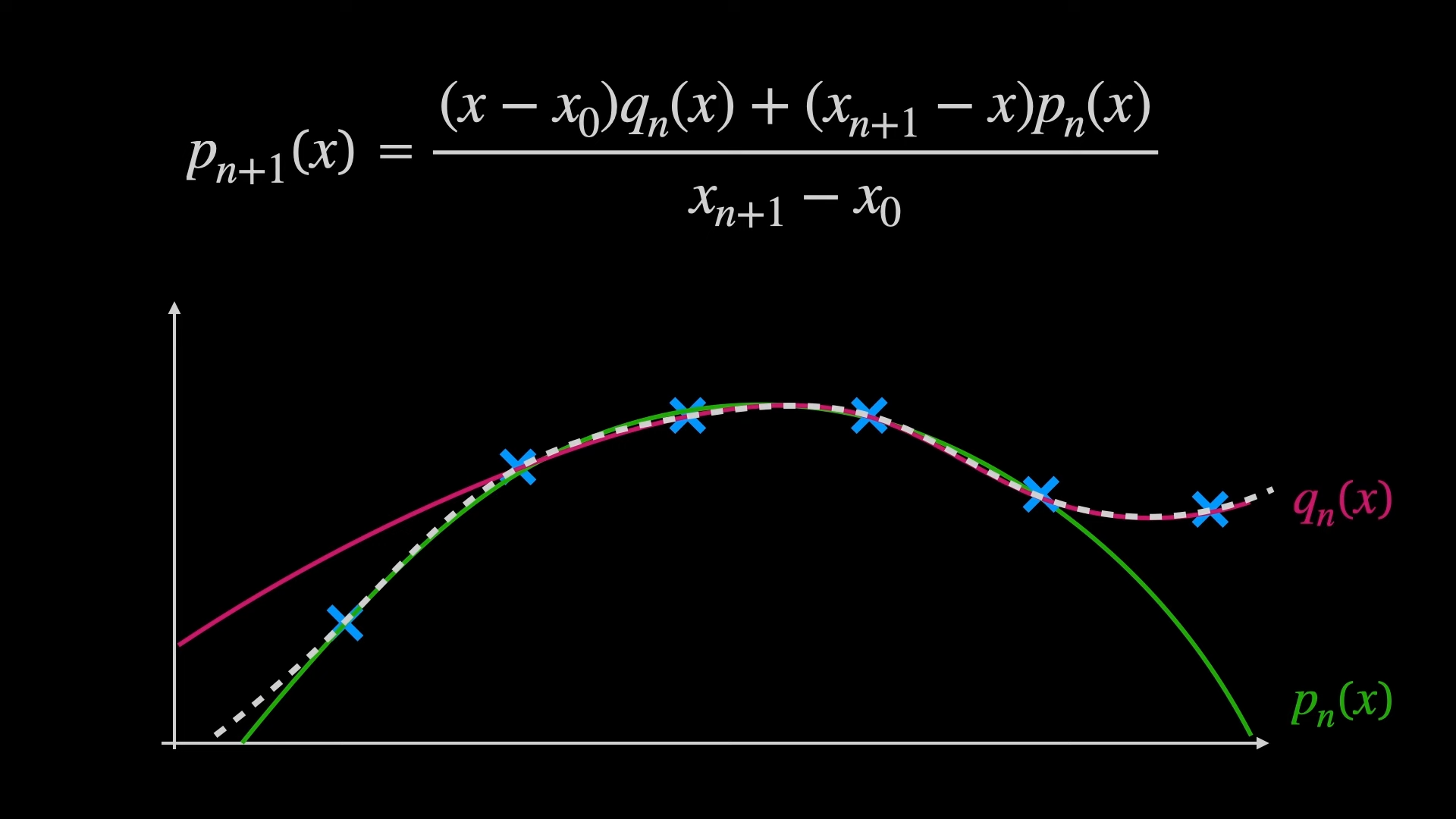
$p_n(x)$를 $0$부터 $n$까지의 점들을 사용해 보간한 함수라고 하고,
$q_n(x)$를 $1$부터 $n+1$까지의 점들을 사용해 보간한 함수라고 합니다.

두 함수를 시각적으로 표현하면 아래와 같습니다.

Dr. Will Wood

이제 두 함수를 조합하여 확장한 함수 $p_{n+1}(x)$를 정의 합니다.

Dr. Will Wood

이 함수는 $0$부터 $n+1$까지 모든 점을 지나갑니다. 그러나 이것이 정말 사실인지 엄밀하게 살펴봐야 합니다.

양 끝점 $x_0$과 $x_{n+1}$에서 함수는 각각 $p_n(x)$와 $q_n(x)$처럼 행동 합니다. 따라서, $p_{n+1}(x)$ 함수는 $x_0$과 $x_{n+1}$를 지나갑니다.

Dr. Will Wood

양 끝점의 사이에 있는 $x_k$에 대해서도 확인해보아야 합니다. 식을 잘 정리하면, $x_k$에서 확장 함수가 $p_n(x_k)$의 값을 가짐을 보일 수 있습니다.

Dr. Will Wood

Proof of Theorem

TODO

vs. Langrage Interpolation

새로운 데이터 노드가 추가될 때, 두 방법의 대응 방식이 다릅니다.

• 라그랑주 보간법
  • 각 점마다 새로운 다항식 항이 생깁니다.
  • 그래서 새로운 데이터 노드가 추가되면, 보간식을 처음부터 다시 계산해야 합니다.
  • 따라서, 점이 추가되는 상황에서는 아주 비효율적입니다.
• 분할 차분 보간법
  • 이전에 계산된 값들을 그대로 활용할 수 있습니다.
  • 새로운 데이터 노드가 들어오면, 새로운 항 하나만 계산하면 됩니다.
  • 그래서 보간 함수의 “실시간 업데이트”가 가능 합니다.

Property

No matter the data points orders

For any permutation $\sigma$ on $\left\{ 1, \dots, n \right\}$,

\[f[x_1, \dots, x_n] = f[x_{\sigma(1)}, \dots, x_{\sigma(n)}]\]

분할 차분 방법은 입력된 $x$들의 순서에 전혀 영향을 받지 않는다는 성질 입니다. 그래서 분할 차분을 계산하거나 표현할 때, 데이터의 순서에서 자유롭습니다.

Connection between Divided Difference and Function’s Differential

Given divided difference $f[x_1, \dots, x_n]$, it can be derived from the $(n-1)$-th derivatives like

\[f[x_1, \dots, x_n] = \frac{f^{(n-1)}(\xi)}{(n-1)!}\]

where $\xi \in \left(\min(\left\{ x_i \right\}), \max(\left\{ x_i \right\})\right)$

가장 간단한 예제는 1차 분할 차분 $f[x_1, x_2]$ 입니다. 이것은

\[f[x_1, x_2] = \frac{f(x_2) - f(x_1)}{x_2 - x_1}\]

를 만족하는데, 이때, “평균값 정리”에 의해

\[f[x_1, x_2] = \frac{f(x_2) - f(x_1)}{x_2 - x_1} = f'(\xi)\]

를 만족하는 $\xi$가 $\xi \in (x_1, x_2)$ 범위 내에 존재합니다. 그래서 이 성질을 “고차 평균값 정리(Generalized Mean Value Theorem)“이라고도 합니다.

Proof: TODO

Finite Differences

\[\Delta f(x) = \frac{f(x+h) - f(x)}{h}\]

요건 곁다리 내용인데요! “유한 차분(finite difference)”라는 것도 있습니다. 분할 차분과 유한 차분의 차이는 등간격 여부 입니다! 유한 차분은 각 데이터 노드의 간격이 일정해야 합니다. 반면, 분할 차분은 데이터 노드의 간격에 대한 제약 조건이 없습니다.

유한 차분도 2차, 3차 차분을 정의할 수 있습니다!

\[\Delta^2 f(x) = \Delta (\Delta f(x)) = f(x+2h) - 2f(x+h) + f(x)\]

참고자료

• ‘섭교수’님의 블로그
• ‘Dr. Will Wood’의 영상