Interpolation for Uniformly Spaced Nodes, Runge Phenomenon

수학과 복수전공을 위해 졸업 마지막 학기에 “수치해석개론” 수업을 듣게 되었습니다. 수학과 졸업시험도 겸사겸사 준비할 겸 화이팅 해봅시다!! 전체 포스트는 “Numerical Analysis“에서 확인할 수 있습니다.

들어가며

지금까지는 주어진 데이터가 균등하게 분포되어 있다면 어떤 좋은 일이 있을까요? 이번 포스트에선 데이터 샘플을 뽑을 때, 균등 샘플링을 했을 때 우리가 무엇을 기대할 수 있는지에 대한 탐구를 다룹니다.

Uniformly Spaced Nodes Interpolation

데이터 노드가 특수하게 배치된 경우를 살펴봅시다.

모든 데이터 노드가 $[a, b]$ 공간 위에 “동일“한 거리만큼 분산 되어 있다고 합시다. 각 점이 떨어진 거리를 $h$라고 한다면, 각 점은 아래와 같이 배치됩니다.

\[x_i = a + i h \quad \text{where} \quad h = \frac{b-a}{n}\]

그리고 보간 오차는 아래와 같이 주어집니다.

\[\| f(x) - I_n f(x) \| \le \frac{\max_{x\in[a, b]} \| \omega_n(x) \| }{n!} M_n\]

Estimate for nodal polynomial error bound

데이터 노드가 균등하게 분배 되어 있다면, nodal polynomial $\omega_n(x)$의 상한을 정확하게 유도할 수 있습니다.

쉽게 진행하기 위해 한점 $x$를 $x = a + hs$로 변수 치환을 합니다. $x$는 데이터 노드 $x_i$가 아니라 임의의 한점인 것에 유의합니다. 그러면 $\omega_n(x)$는 아래와 같이 다시 작성 됩니다.

\[\begin{aligned} \omega_n(x) &= \prod_{j=1}^n (x-x_j) \\ &= \prod_{j=1}^n \left((a + hs)-(a + hj)\right) \\ &= \prod_{j=1}^n h(s - j) \\ &= h^n \prod_{j=1}^n (s - j) \end{aligned}\]

오차 상한 $W$를 정의 합니다.

\[\begin{aligned} W &= \max_{x\in[a, b]} \| \omega_n (x) \| \\ &= \max_{s \in (0, n)} \left\{h^n \prod_{j=1}^n \| s - j \|\right\} \\ &= h^n \cdot \max_{s \in (0, n)} \left\{\prod_{j=1}^n \| s - j \|\right\} \end{aligned}\]

즉, 아래의 곱의 최대값을 구하는 것이 목표 입니다.

\[\prod_{j=1}^n \| s - j \|\]

이것을 구하기 위해 약간의 트릭을 써야 합니다. $s \in (0, n)$는 구간 내에 있는 어떤 실수 입니다. 그래서 어떤 정수 $i \in [0, n]$에 대해 $i < s < i+1$를 만족 합니다. 이 정수 $i$를 기준으로 곱을 나눠줍니다.

\[\begin{aligned} \prod_{j=1}^n \| s - j \| = \left(\prod_{j=1}^{i-1} \| s - j \|\right) \cdot \left( s - i \right) \cdot \left( s - (i+1) \right) \cdot \left( \prod_{j=i+2}^{n} \| s - j \| \right) \end{aligned}\]

절댓값이 있는 부분만 오차 한계를 계산해보면 아래와 같습니다.

\[\|(s-j)(s-(i+1))\| \le \frac{1}{4}\]

그리고 곱의 앞 부분을 살펴보면, $s \le i+1$라는 성질을 활용해 아래와 같은 부등식이 유도 됩니다.

\[\prod_{j=1}^{i-1} \| s - j \| = \prod_{j=1}^{i-1} ( s - j ) \le \prod_{j=1}^{i-1} ( i + 1 - j ) = (i+1)!\]

그리고 곱의 뒷 부분을 살펴보면, $s > i$이기 때문에,

\[\prod_{j=i+2}^{n} \| s - j \| = \prod_{j=i+2}^{n} (j - s) \le \prod_{j=i+2}^{n} (j - i) = (2)(3)\cdots(n-i) \le (i+2)(i+3)\cdots n\]

따라서, 곱의 오차 한계는 아래와 같이 정리 됩니다.

\[\begin{aligned} \prod_{j=1}^n \| s - j \| &= \left(\prod_{j=1}^{i-1} \| s - j \|\right) \cdot \left( s - i \right) \cdot \left( s - (i+1) \right) \cdot \left( \prod_{j=i+2}^{n} \| s - j \| \right) \\ &\le (i+1)! \cdot \frac{1}{4} \cdot \left\{(i+2)(i+3)\cdots n\right\} \\ &= \frac{1}{4} n! \end{aligned}\]

따라서, 아래의 식이 성립합니다.

\[\max \omega_n(x) = W \le h^n \frac{1}{4} n!\]

정리하면,

\[\|f(x) - I_n f(x) \| \le \frac{h^{n}}{4 n!} \max_{x \in [a, b]} \| f^{(n+1)} (x) \|\]

Runge Phenomenon

수학자 “Runge”가 제시한 함수로, 보간법에서 발생하는 아주 유명한 문제 사례 입니다.

Runge는 아래와 같은 간단 함수를 제시 합니다.

\[f(x) = \frac{1}{1+12 x^2}\]

이 함수를 매끄럽고, 전체적으로 잘 생긴 종 모양 함수 입니다. 그런데, 이걸 균등하게 나눈 노드(equally spaced nodes)를 사용해 다항식으로 보간하면 심각한 문제가 발생 합니다!

이 문제는 다항 보간에서, 노드가 균등하게 배치되어 있고 보간 함수의 차수가 높아질수록, 함수 양 끝단에서 보간 다항식이 심하게 진동하는 현상 입니다.

즉, 중심 쪽은 보간이 잘 맞는데 비해, 양 끝 구간에서는 크게 진동(wiggle) 해버립니다.

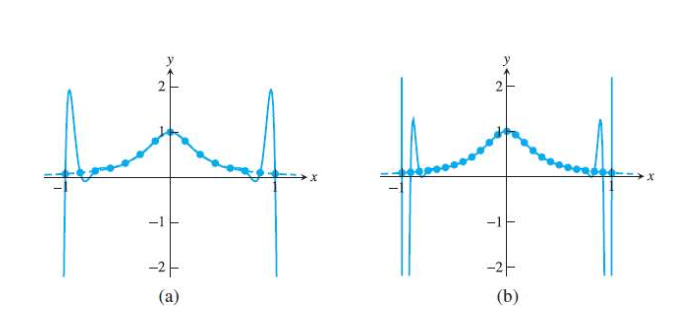
이 현상을 해결하기 위해 등장한 것이 Piecewise Interpolation 방식인 “Spline” 입니다! 다음 포스트에선 이 Spline 보간법에 대해 살펴보겠습니다.

➡️ Spline Interpolation