Cubic Spline

수학과 복수전공을 위해 졸업 마지막 학기에 “수치해석개론” 수업을 듣게 되었습니다. 수학과 졸업시험도 겸사겸사 준비할 겸 화이팅 해봅시다!! 전체 포스트는 “Numerical Analysis“에서 확인할 수 있습니다.

들어가며

지금까지는 하나의 Polynomial을 통해 주어진 데이터를 보간하였습니다. 그러나 이것은 높은 차수의 Polynomial을 만들게 했고, 이로 인해서 “Runge Effect“와 같이 함수가 크게 어긋나는 현상도 볼 수 있었습니다.

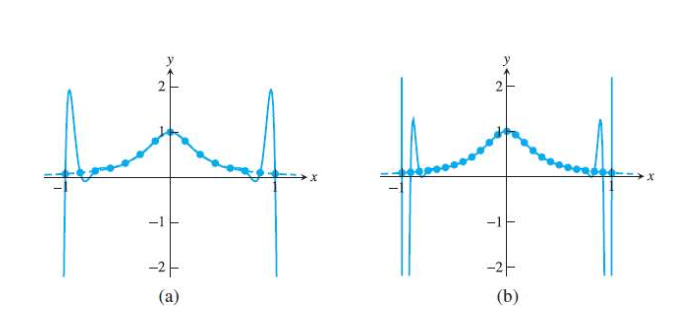
이에 대한 대안으로 나온 것이 “Piecewise-Polynomial Approximation”입니다. 이 접근은 각 구간을 낮은 차수의 $n$차 다항식으로 근사하고 이들을 모음으로써 근사 함수를 얻습니다.

1차 스플라인 (Linear)

Piecewise-Linear Interpolation 방법 입니다.

단순히 주어진 데이터 노드 $(x_1, y_1), \dots, (x_n, y_n)$를 서로 이어주는 라인을 그려주면 됩니다. 수학적으로는

$S(x)$는 각 구간 $[x_j, x_{j+1}]$ 별로 $S_j(x)$ 함수를 정의합니다. 이때, 각 구간 함수 $S_j(x)$는 아래를 만족해야 합니다.

• $S_j(x_j) = f(x_j) = S_j(x_{j+1}) = f(x_{j+1})$
• $S_{j}(x_{j+1}) = S_{j+1}(x_{j+1})$

그러나, 단점은 이 보간 함수는 각 데이터 노드에서 미분 불가능한 함수 입니다. 가장 간단한 방법이지만 그만큼 스무스 하지 않은 근사법입니다.

2차 스플라인 (Quadratic)

이번에는 각 구간 함수를 2차 함수로 근사하는 방법 입니다. 그리고 위의 Piecewise-Linear에서 아래의 조건만 추가 되면 됩니다.

• $S_{j}’(x_{j+1}) = S_{j+1}’(x_{j+1})$

도함수의 값을 고려해 근사를 하는 방식 입니다만, 곡률(2차 도함수)가 연속이 아닙니다. 곡률이 불연속하면 부드러운 곡선의 느낌이 나지 않고 시각적으로도 부자연스러움이 생긴다고 합니다.

그래서 보통은 3차 함수로 근사하는 Cubic Spline 근사가 자주 사용 됩니다.

3차 스플라인 (Cubic)

이번에는 각 구간 함수를 3차 함수로 근사하는 방법 입니다. 곡률에 대한 부분인 2차 도함수에 대한 조건이 추가 됩니다.

• $S_{j}’‘(x_{j+1}) = S_{j+1}’‘(x_{j+1})$

Cubic Spline은 곡률의 연속성이라는 나이스한 조건을 가지고 있기 때문에, 가장 자주 사용되는 스플라인 근사 기법 입니다. 그래서 앞으로의 논의는 모두 Cubic Spline을 기준으로 진행하도록 하겠습니다.

Boundary Condition

이때, 조금더 스무스한 느낌을 주기 위해 경계 노드 $x_0$, $x_n$에서 추가 조건을 만족하도록 근사 할 수 있습니다.

• Natural Boundary
  • $S’‘(x_0) = S’‘(x_n) = 0$
• Clamped Boundary
  • $S’(x_0) = f’(x_0)$ and $S’(x_n) = f’(x_n)$
  • 참고로 “clamp”는 집게라는 뜻 입니다. 스플라인 곡선의 양 끝단을 고정하는 기법이라는 말 입니다.

Number of Constants

주어진 $n$개 데이터 노드 $(x_1, y_1), \dots, (x_n, y_n)$에 대해 $(n-1)$개의 Cubic polynomial은 아래와 같이 정의 됩니다.

\[\begin{aligned} S_1(x) &= a_1 + b_1(x-x_1) + c_1(x-x_1)^2 + d_1(x-x_1)^3 \\ S_2(x) &= a_2 + b_2(x-x_2) + c_2(x-x_2)^2 + d_2(x-x_2)^3 \\ &\vdots \\ S_{n-1}(x) &= a_{n-1} + b_{n-1}(x-x_{n-1}) + c_{n-1}(x-x_{n-1})^2 + d_{n-1}(x-x_{n-1})^3 \\ \end{aligned}\]

즉, Cubic Spline을 구축하기 위해선 $4(n-1)$개의 상수 값들을 알아내야 합니다. 그런데 Cubic Spline을 구하기 위해서는 $4(n-1)$ 전부가 아니라 오직 $c_j$의 값만 모두 계산할 수 있다면 나머지 $a_j, b_j, d_j$의 값도 계산할 수 있다는 것이 증명 되어 있습니다!

Uniqueness of Natural Cubic Spline

IF $f$ is defined at $a = x_1 < \cdots < x_n = b$,

then $f$ has a “unique natural spline” interpolant $S$ on the nodes $x_1, \dots, x_n$;

that is, a spline interpolant that satisfies the natural boundary conditions $S’‘(a) = S’‘(b) = 0$.

Proof

⚠️ 주의! 이어지는 증명은 정신을 아득하게 만듭니다…

Spline 제약 조건에 따라 아래의 식이 성립 합니다.

\[a_j = y_j = S_j(x_j)\]

즉, 모든 $a_j$의 값은 데이터 노드의 $y_j$ 값을 통해서 구할 수 있습니다. 이것은 $4(n-1)$개 상수 중에 $a_j$에 해당하는 $(n-1)$개는 구할 필요가 없다는 것을 말합니다.

인접한 스플라인은 $S_j(x_{j+1}) = S_{j+1}(x_{j+1})$가 성립해야 합니다.

\[\begin{aligned} S_j(x_{j+1}) &= a_j + b_j(x_{j+1} - x_j) + c_j(x_{j+1}-x_j)^2 + d_j(x_{j+1}-x_j)^3 \\ S_{j+1}(x_{j+1}) &= a_{j+1} \end{aligned}\]

다시 정리하면,

\[a_{j+1} = a_j + b_j(x_{j+1} - x_j) + c_j(x_{j+1}-x_j)^2 + d_j(x_{j+1}-x_j)^3\]

인데, $h_j = x_{j+1} - x_j$라고 하고, $\Delta_j = y_{j+1} - y_j = a_{j+1} - a_j$라고 합시다. 참고로 $h_j$와 $\Delta_j$ 둘다 데이터 노드에서 얻을 수 있는 상수값 입니다. 그러면,

\[\begin{aligned} a_{j+1} &= a_j + b_j h_j + c_j h_j^2 + d_j h_j^3 \\ a_{j+1} - a_j &= b_j h_j + c_j h_j^2 + d_j h_j^3 \\ \Delta_j &= b_j h_j + c_j h_j^2 + d_j h_j^3 \\ \end{aligned}\]

이것을 $b_j$에 대해 정리해보면 아래와 같습니다.

\[b_j = \frac{\Delta_j}{h_j} - c_j h_j - d_j h_j^2\]

(여기에서 미지수는 $c_j$와 $d_j$ 뿐인 것을 유념 합니다)

도함수에 대해서도 동일하게 스플라인의 제약 조건으로 등식을 세워봅시다. 그러면,

\[\begin{aligned} S_j'(x_{j+1}) &= b_j + 2 c_j(x_{j+1}-x_j) + 3 d_j(x_{j+1}-x_j)^2 = b_j + 2c_j h_j + 3 d_j h_j^2 \\ S_{j+1}'(x_{j+1}) &= b_{j+1} \end{aligned}\]

스플라인의 성질에 의해 $S_j’(x_{j+1}) = S_{j+1}’(x_{j+1})$

\[b_{j+1} = b_j + 2 c_j h_j + 3d_j h_j^2\]

(참고로 위의 등식이 가장 마지막에 사용됩니다… ㅋㅋ)

마지막으로 곡률에 대해서도 아래의 식이 성립한다.

\[\begin{aligned} S_j''(x_{j+1}) &= 2 c_j(x_{j+1}-x_j) + 6 d_j(x_{j+1}-x_j) = 2 c_j + 6d_j h_j \\ S_{j+1}''(x_{j+1}) &= 2 c_{j+1} \end{aligned}\]

따라서,

\[c_j + 3 d_j h_j = c_{j+1}\]

이걸 $d_j$에 대해서 정리하면,

\[d_j = \frac{c_{j+1} - c_j}{3 h_j}\]

아까 위에서 $b_j$을 미지수 $c_j$와 $d_j$로 표현했던 것을 기억하나요? 거기에서 $d_j$를 $c_j$에 대한 식으로 바꾸면 $b_j$도 $c_j$에 대한 식으로만 표현할 수 있습니다.

\[\begin{aligned} b_j &= \frac{\Delta_j}{h_j} - c_j h_j - d_j h_j^2 \\ &= \frac{\Delta_j}{h_j} - c_j h_j - \frac{c_{j+1} - c_j}{3 h_j} h_j^2 \\ &= \frac{\Delta_j}{h_j} - \frac{h_j}{3}(2c_j + c_{j+1}) \end{aligned}\]

위의 등식은 만약 $c_j$, $c_{j+1}$의 값을 안다면, $b_j$의 값을 결정할 수 있다는 것을 말합니다.

결국, $4(n-1)$개 상수 중에서

• $a_j$는 데이터 노드로 결정했고,
• $d_j$는 $c_j$, $c_{j+1}$의 값으로 결정하고,
• $b_j$도 $c_j$, $c_{j+1}$의 값으로 결정합니다.

그래서 Cubic Spline을 구하기 위해선 “모든 $c_j$의 값만 결정하면 나머지 값들은 따라서 결정” 됩니다.

---

$c_j$에 대한 방정식을 세우기 위해 도함수에 대한 등식 $b_{j+1} = b_j + 2 c_j h_j + 3d_j h_j^2$를 활용해봅시다. $b_j$에 $c_j$들을 대입해줍니다.

\[\frac{\Delta_{j+1}}{h_{j+1}} - \frac{h_{j+1}}{3}(2c_{j+1} + c_{j+2}) = \left( \frac{\Delta_{j}}{h_{j}} - \frac{h_{j}}{3}(2c_{j} + c_{j+1}) \right) + 2 c_j h_j + 3 \left( \frac{c_{j+1} - c_j}{3 h_j} \right) h_j^2\]

이 식을 $c_j, c_{j+1}, c_{j+2}$에 대한식으로 잘 정리해봅시다.

\[\begin{aligned} \left( \frac{2 h_j}{3} - 2 h_j + h_j \right) c_j + \left( - \frac{2h_{j+1}}{3} + \frac{h_j}{3} - h_j \right) c_{j+1} + \left( - \frac{h_{j+1}}{3} \right) c_{j+2} &= \left( - \frac{\Delta_{j+1}}{h_{j+1}} + \frac{\Delta_j}{h_j} \right) \\ \left( - h_j \right) c_j + 2 \left( - h_{j+1} - h_j \right) c_{j+1} + \left( - h_{j+1} \right) c_{j+2} &= 3 \left( - \frac{\Delta_{j+1}}{h_{j+1}} + \frac{\Delta_j}{h_j} \right) \\ h_j \cdot c_j + 2 \left( h_{j+1} + h_j \right) \cdot c_{j+1} + h_{j+1} \cdot c_{j+2} &= 3 \left( \frac{\Delta_{j+1}}{h_{j+1}} - \frac{\Delta_j}{h_j} \right) \end{aligned}\]

식을 전개 하는 과정이 어지러웠지만, 결국 핵심은 이런 일반항 관계가 나온다는 것이다. 이 일반항 관계는 이웃한 세 개의 $c$ 값들 간의 선형관계를 말해줍니다.

\[h_j \cdot c_j + 2 \left( h_{j+1} + h_j \right) \cdot c_{j+1} + h_{j+1} \cdot c_{j+2} = 3 \left( \frac{\Delta_{j+1}}{h_{j+1}} - \frac{\Delta_j}{h_j} \right)\]

그리고 이 선형 관계를 통해 선형 방정식을 유도할 수 있습니다.

\[A\mathbf{c} = \mathbf{b}\]

where

\[A = \left( \begin{matrix} 1 & 0 & 0 \\ h_1 & 2 (h_1 + h_2) & h_2 & \ddots \\ 0 & h_2 & 2(h_2 + h_3) & h_3 & \ddots \\ & \ddots & \ddots & \ddots & \ddots \\ & & & h_{n-2} & 2 (h_{n-2} + h_{n-1}) & h_{n-1} \\ & & & 0 & 0 & 1 \end{matrix} \right)\]

그리고

\[\mathbf{c} = \left( \begin{matrix} c_1 \\ c_2 \\ \vdots \\ c_{n-1} \\ c_n \end{matrix} \right) , \quad \mathbf{b} = \left( \begin{matrix} 0 \\ 3 \left(\frac{\Delta_2}{h_2} - \frac{\Delta_1}{h_1}\right) \\ \vdots \\ 3 \left(\frac{\Delta_{n-1}}{h_{n-1}} - \frac{\Delta_{n-2}}{h_{n-2}}\right) \\ 0 \end{matrix} \right)\]

이때, $A$ 행렬에 $\left(1, 0, 0\right)$ 파트가 있는 이유는 Natural Cubic Spline 이기 때문에, $c_1 = c_n = 0$을 만족해야 하기 때문이다.

행렬 $A$가 삼대각 행렬이기 때문에, $A\mathbf{c} = \mathbf{b}$에는 Unique Solution이 존재한다. 삼대각(tridiagnoal) 행렬이라는 것은 대각선과 그 바로 위의 대각선과 그 바로 아래의 대각선만이 0이 아닌 값을 가지는 행렬을 말합니다. 참고로 일반적인 $n\times n$ 선형 방정식을 가우스 소거법으로 풀면 $O(n^3)$의 계산량이 필요하지만, 삼대각 시스템은 “Thomas Algorithm”이라는 특별한 알고리즘을 통해 $O(n)$ 시간 안에 해결 가능 합니다!

이것은 곧 Natural Cubic Spline에 대한 유일해가 존재함을 말한다.

Degree of Freedom

스플라인 근사를 구하기 위해서 처음에는 $4(n-1)$개의 상수를 구하는 것으로 시작 했습니다. 그러나 실제로는 $c_j$읙 값만 알, 나머지 $a_j$, $b_j$, $d_j$도 모두 구할 수 있으므로, 문제는 $c_j$들을 구하는 문제로 환원 되었습니다.

게다가 $c_j$에 대한 일반항 관계는 이웃한 세 개의 $c$ 값들 간의 선형 관계를 보여주며,

\[h_j \cdot c_j + 2 \left( h_{j+1} + h_j \right) \cdot c_{j+1} + h_{j+1} \cdot c_{j+2} = 3 \left( \frac{\Delta_{j+1}}{h_{j+1}} - \frac{\Delta_j}{h_j} \right)\]

이를 통해 $c_1, \dots, c_n$을 구하는 선형 방정식 시스템을 유도할 수 있었다.

\[A \mathbf{c} = \mathbf{b}\]

이 관계식은 삼대각 연립방정식이 되며, 여기에서 $A$는 삼대각 행렬로 계산이 $O(n)$ 밖에 걸리지 않습니다.

결국 $4(n-1)$를 구하는 문제는 $c_1, .., c_n$개 변수로 구성된 문제로 환원 되었으며, Natural Boundary 조건 $c_1 = c_n = 0$이 있다면, 최종적으로 $(n-2)$의 자유도를 갖는 선형 시스템으로 환원 됩니다.

Clamped Cubic Spline

참고로 Spline의 유일성은 Clamped Spline에서도 성립 합니다.

맺음말

Spline은 예전에 “Statistical Data Mining(IMEN472)” 수업 때 배웠던 과목인게 생각이 납니다. 그때는 수업 내용이 진짜 하나도 머릿속에 들어오지 않았는데 ㅋㅋㅋ 수치해석개론을 먼저 듣고, 그 과목을 들었다면 더 재밌게 수업을 들었을 것 같네요. 당시에 저 수업 듣고 막 회사에 들어가서 첫 인턴 업무로 받는 것에 “Cubic Spline”을 적용 했던 기억도 새록새록 납니다 ㅋㅋ (그때는 멋인 DS가 되어 있을 줄 알았는데…)

암튼 다시 봐서 반가운 친구였구요! 내일이 중간고사인데 이제 이걸 보고 있습니다… ㅋㅋ 화이팅!!