Bundle of Goods

졸업을 위해 마지막 학기에 “미시경제학” 수업을 듣게 되었습니다. 경제학원론 수업을 재밌게 들어서 경제 쪽이랑 궁합이 좋은 줄 알고 신청 했는데, 웬걸… 이 과목은 사실상 수학과 과목 이었습니다.. ㅋㅋ 그래도 어영부영 수학과 복수전공을 하고 있으니, 이 수업도 힘내서 잘 들어봅시다! 전체 포스트는 “미시경제학” 카테고리에서 확인하실 수 있습니다.

Bundle

소비자는 두 재화를 선택할 수 있습니다. 그리고, 그 재화를 선택하는 조합을 $X = \mathbb{R}^2_{+}$라고 하면, 그 묶음(bundle)은 $(x_1, x_2) \in X$로 표현 됩니다. 번들은 이 가능한 모든 조합들을 말합니다.

예를 들어,

• $(3, 0)$: 3개의 감자, 0개의 고구마
• $(1, 2)$: 1개의 감자, 2개의 고구마
• $(0, 0)$: 아무것도 없음. (가능한 선택이지만 선호하지 않음)

물리적인 재화를 묶어 번들을 구상할 수도 있지만, 추상적인 대상으로도 구상할 수 있습니다.

• 시간: 여가 시간 vs. 일하는 시간
• 행복: 나의 행복 vs. 아내의 행복

번들은 이런 조합을 2차원의 좌표로 표현하는 개념이자 접근 입니다.

Bundle Space

아까 번들이 이루는 조합은 선택 공간 $X = \mathbb{R}^2_{+}$를 사용한다고 했습니다. 이 이걸 사용하는지, 그리고 이 선택 공간 위에서의 연산이 어떤 의미를 갖는지 살펴봅니다.

Continuous

감자 $1/2$개, 자동차 $0.2$대를 선택할지 논의하는게 의미가 있을까?

대부분의 상품은 이산(discrete)적으로 거래 됩니다. 그런데, $\mathbb{R}^2_{+}$ 공간은 연속(continuous) 공간 입니다.

이것은 모델링의 편의상 번들의 공간을 “연속적”으로 간주하는 것 입니다. 실제 세상에서는 물건을 쪼갤 수 없지만, 경제학에서는 계산과 이론 전개의 편의를 위해 이렇게 설정 한다고 합니다.

재화의 양을 연속 변수로 생각한다면, 미분(differential)이 가능하고, 수학적 분석이 쉬워집니다.

Algebraic Operations

재화의 묶음(bundle)을 수학적으로 쉽게 조작할 수 있습니다.

두 묶음을 하나로 합치는 것과 묶음을 비율만큼 확장하거나 축소하는 연산을 정의할 수 있습니다.

\[\mathbf{x} + \mathbf{y} = (x_1 + y_1, x_2 + y_2)\] \[\lambda \mathbf{x} = (\lambda x_1, \lambda x_2)\]

Preference over bundles

소비자는 여러 소비 묶음 중에 어떤 것을 더 선호할 수 있습니다.

이런 선호 관계는 무차별 집합 또는 무차별 곡선(indifference curve)를 통해 표현할 수도 있습니다.

어떤 번들 $\mathbf{a}$에 대해 무차별적인 번들의 집합은 아래와 같습니다.

\[\left\{ \mathbf{y} \in X : \mathbf{y} \sim \mathbf{a} \right\}\]

여기서 $\mathbf{y} \sim \mathbf{a}$는 번들 $\mathbf{y}$와 $\mathbf{a}$가 소비자에게 동일한 만족감을 준다는 의미 입니다.

만약 선호 관계를 효용 함수 $u$로 표현할 수 있다면, 무차별 집합은 아래와 같습니다.

\[\left\{ \mathbf{y} \in X : u(\mathbf{y}) = u(\mathbf{a}) \right\}\]

그리고 이 $\mathbf{y}$가 그리는 연속적인 곡선을 효용 함수의 “등고선(contour)“으로 해석할 수 있습니다.

Constant Tradeoff

소비자는 두 재화에 대해 효용값 $v_1$, $v_2$를 가지고 있습니다.

번들에 대한 선호 관계는 아래와 같이 정의 됩니다.

\[\mathbf{x} \succcurlyeq \mathbf{y} \iff v_1 x_1 + v_2 x_2 \ge v_1 y_1 + v_2 y_2\]

그리고 효용 함수는 아래와 같이 정의 됩니다.

\[u(x) = v_1 x_1 + v_2 x_2\]

이 효용 함수의 “무차별 곡선”은 아래와 같이 정의 됩니다.

\[\left\{ (x_1, x_2) \in X : v_1 x_1 + v_2 x_2 = v_1 a_1 + v_2 a_2 \right\}\]

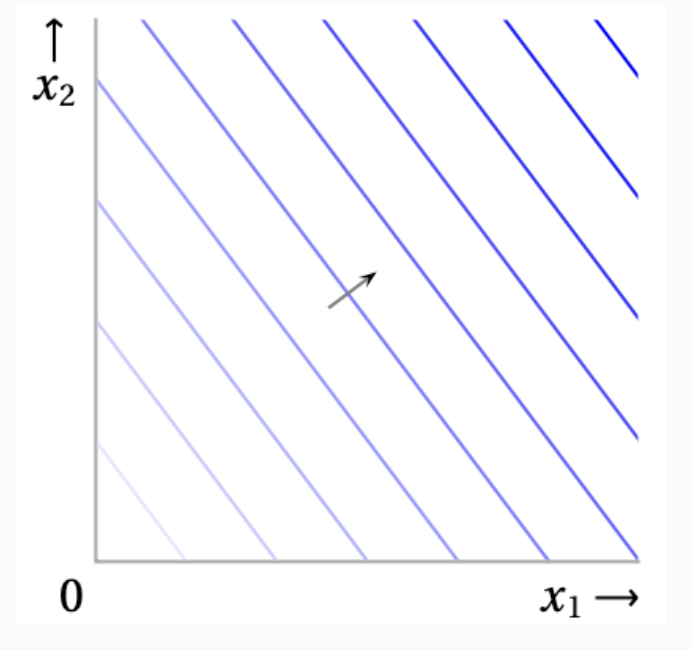
위의 그림은 무차별 곡선을 표현한 것으로 직선으로 표현 됩니다. 그리고 같은 직선 위에 있는 번들은 서로 무차별하게 선호 됩니다.

그리고 화살표는 무차별 직선 사이에 선호 관계를 표현 합니다. 위쪽과 오른족으로 갈수록 더 선호 되는 번들 조합 입니다.

Only Preference

소비자가 오직 하나의 재화에만 관심이 있을 수 있습니다. 두번재 재화 $x_2$에만 관심이 있다고 한다면, 번들을 구성할 때, $x_1$의 값은 상관이 없습니다. 그래서 효용 함수는 $u(x) = x_2$로 정의되고, 무차별 곡선이 아래와 같이 정의 됩니다.

\[\left\{ (x_1, x_2) \in X : x_2 = c \right\}\]

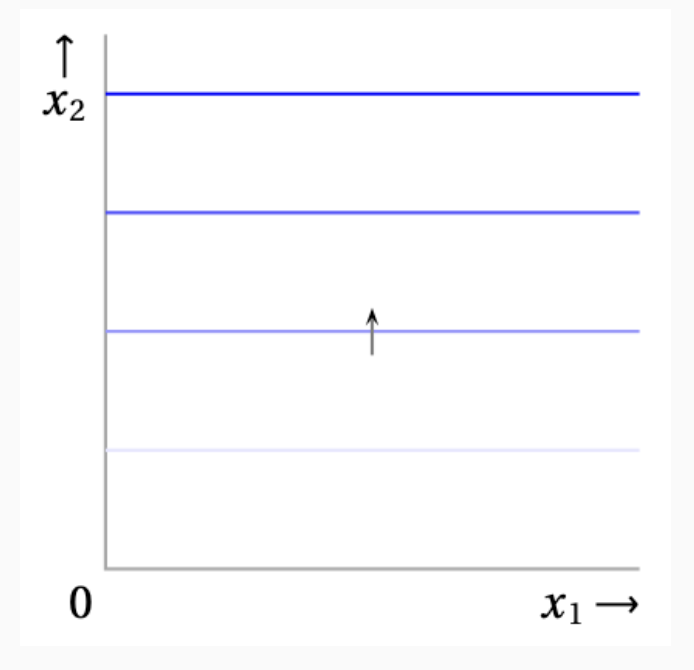
이런 경우는 $x_1$이 아무리 변해도 $x_2$가 같다면, 소비자에게 동일한 만족을 줍니다. 그리고 무차별 곡선은 모두 “수평선”으로 그려집니다.

그리고 화살표는 무차별 곡선이 더 많은 $x_2$를 주는 방향으로 선호한다는 것을 알려줍니다.

Stepwise Preference

첫번째 재화가 특성 수준이 될 때까지는 첫번째 재화만 신경 쓰고, 그 이후부터는 두번째 재화만 신경 쓰는 특이한 선호 구조 입니다.

소비자는 처음에 첫번쨰 재화의 양만 신경 씁니다. 그 양이 10을 초과하기 전까지는 두번째 재화에는 관심도 없습니다.

\[(x_1, x_1) \succcurlyeq (y_1, y_2) \quad \text{if} \quad \quad y_1 \le 10 \quad \text{and} \quad x_1 \ge y_1\]

첫번재 재화가 10보다 많아지면, 그 이후부터는 두번째 재화의 양이 소비자의 선호를 결정 합니다.

\[(x_1, x_1) \succcurlyeq (y_1, y_2) \quad \text{if} \quad \quad x_1, y_1 > 10 \quad \text{and} \quad x_2 \ge y_2\]

이걸 효용 함수로 표현하면 아래와 같습니다.

\[u(x_1, x_2) = \begin{cases} x_1 & \text{if} \quad x_1 \le 10 \\ 11 + x_2 & \text{if} x_1 > 10 \end{cases}\]

무차별 곡선은 아래와 같이 그려집니다.

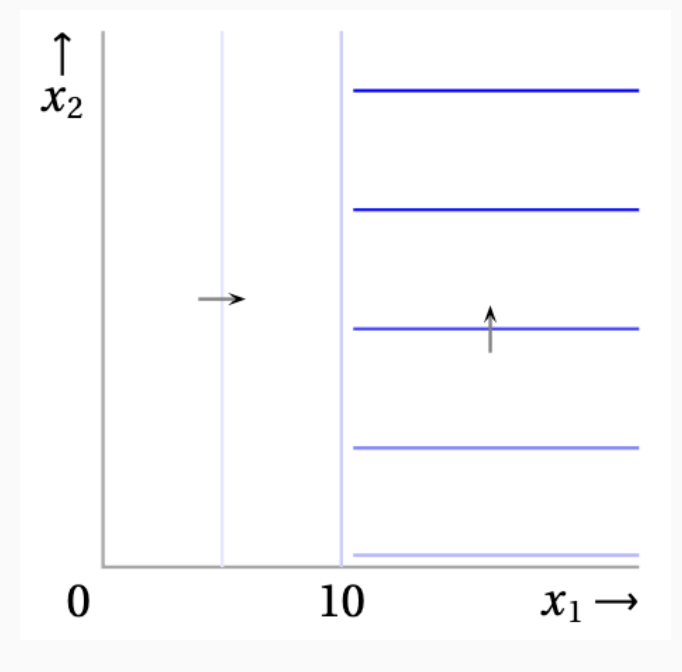
$x_1 \le 10$까지는 곡선이 수직선의 형태로 표현 됩니다. $x_1$의 양만으로 선호가 결정 됩니다.

$x_1 > 10$이 되면, 곡선이 수평선의 형태가 됩니다. $x_2$의 양만으로 선호가 결정 됩니다.

그러한 효용의 형태를 “단계적 선호(stepwise preference)”라고 합니다. 그리고 위에서 살펴본 경우와 달리 “비연속적” 형태를 보입니다.

Complementary Goods

“보완재(Complementary)”는 두 재화를 함께 소비해야만 효용이 올라가는 경우 입니다.

소비재는 두 재화를 동일한 양만큼 가지고 싶어 합니다. 예를 들어, 왼쪽 신발과 오른쪽 신발처럼 둘이 짝이 맞아야 제대로 사용할 수 있습니다. 한 쪽 신발이 많아봐야 소용 없습니다.

이런 번들의 경우, 소비자의 효용은 두 재화 중 더 적은 쪽의 수량에 의해 결정 됩니다. 즉,

\[u(x_1, x_2) = \min (x_1, x_2)\]

무차별 곡선은 “꺽쇠” 형태를 띄게 됩니다.

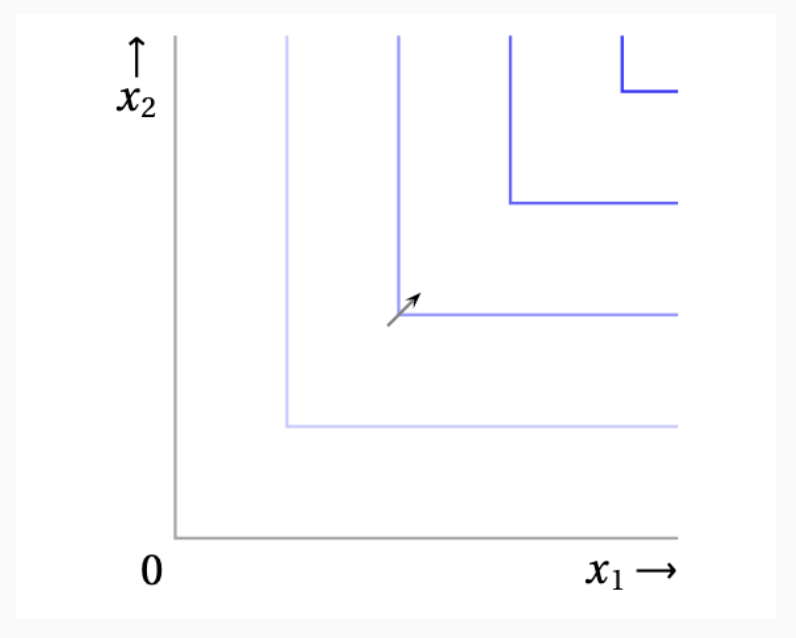
번들 $(2, 5)$와 $(2, 2)$는 동일한 효용을 줍니다. 그 이유는 둘다 최소 재화의 갯수가 2이기 때문입니다.

무차별 곡선 상의 점들은 모두 동일한 $\min(x_1, x_2)$ 값을 가지고 있습니다. 그래서 이 곡선 $x_1 = x_2$를 기준으로 수직/수평으로 뻗어나가는 꺽쇠 형태로 구성 됩니다.

두 재화는 쌍으로 사용되어야 하기 때문에, 한 재화를 아무리 많이 가져도 다른 재화가 없으면 의미가 없습니다. 그리고 번들에 대한 선호는 더 많은 쌍이 있을수록 더 선호되는 방향을 갖습니다.

이번에 살펴본 번들은 두 재화가 “완전한 보완재(perfect complements)” 관계에 있는 재화입니다.

Ideal Bundle

소비자가 번들의 선택 집합 $X$에서 이상적인 번들을 마음속에 가지고 있을 때의 선호 구조를 살펴봅니다.

소비자는 어떤 이상적인 조합 $\mathbf{x}^\ast = (x_1^\ast, x_2^\ast)$을 선호 합니다.

그리고 어떤 두 번들이 주어지면, 그 번들이 이상적인 조합 $\mathbf{x}^\ast$와 더 가까울수록 선호 됩니다. 거리의 척도는 정하기에 따라 달라질 수 있지만, 여기에서는 절댓값 거리인 L1-distance로 표현하겠습니다.

\[\begin{gather*} \mathbf{x} \succcurlyeq \mathbf{y} \\ \iff \\ \| x_1 - x_1^\ast \| + \| x_2 - x_2^\ast \| \le \| y_1 - x_1^\ast \| + \| y_2 + x_2^\ast \| \end{gather*}\]

이 선호를 표현하는 효용 함수는 아래와 같습니다.

\[u(x_1, x_2) = - \left( \| x_1 - x_1^\ast \| + \| x_2 - x_2^\ast \| \right)\]

이것은 이상적인 점에서 멀어질수록 효용이 낮아지는 것을 표현 합니다.

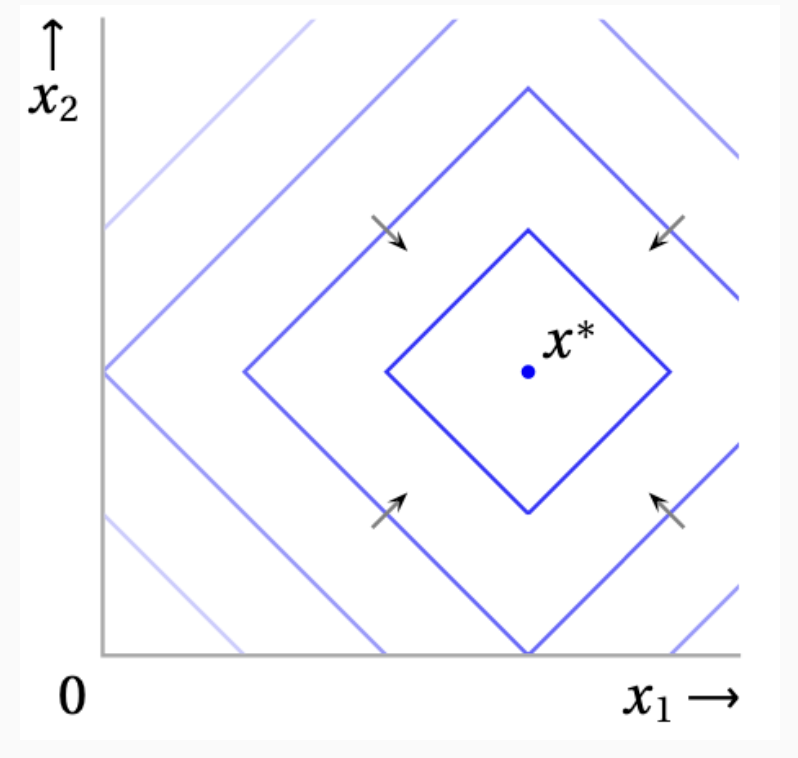
무차별 곡선으로 표현하면 위와 같습니다. 중앙의 점 $\mathbf{x}^\ast$는 이상적인 번들을 나타냅니다. 주변에 그려진 파란색 마름모는 무차별 곡선으로 “같은 거리”를 가진 번들의 집합 입니다.

중심에서 멀어질수록 효용은 떨어지고, 중심 방향의 번들이 더 선호 됩니다.

Lexicographic Preference

사전식 선호 구조입니다. 이 선호 구조는 일반적인 효용 함수로는 표현할 수 없는 중요한 예외 사례 입니다.

소비자는 첫번째 재화를 절대적으로 우선시 합니다. 오직 첫번째 재화의 양만으로 우열을 가리고, 첫번째 재화의 양이 동일한 경우에만 두번째 재화를 기준으로 판단 합니다.

\[\begin{gather*} \mathbf{x} \succcurlyeq \mathbf{y} \\ \iff \\ \begin{cases} x_1 > y_1 \quad \text{or} \\ x_1 = y_1 \quad \text{and} \quad x_2 \ge y_2 \end{cases} \end{gather*}\]

사전식 선호에서는 어떤 두 번들이 주어지는 항상 하나가 더 선호 됩니다. 그래서 “무차별 곡선이 존재하지 않습니다!” 어떤 번들과 무차별한 번들은 그 번들 자신 밖에 없기 때문입니다!

이런 선호는 연속적이지 않고, 비선형적이기 때문에 어떤 효용 함수로도 표현할 수 없습니다.

사전식 선호에서는 번들에서 첫번째 재화가 아주아주아주 조금만 증가해서 선호가 바뀌어 버립니다. 그래서 연속성이 존재하지 않는다고 말하기도 합니다.

맺음말

지금까지 번들의 정의와 번들 위에서 정의되는 선호에 대해 살펴보았습니다. 아직 내용이 남았습니다… ㅋㅋ

이어지는 포스트에서는 번들의 성질들을 살펴보겠습니다.

• Monotonicity
• Continuity
• Convexity
• Differentiability