Bundle Preference: Convexity

졸업을 위해 마지막 학기에 “미시경제학” 수업을 듣게 되었습니다. 경제학원론 수업을 재밌게 들어서 경제 쪽이랑 궁합이 좋은 줄 알고 신청 했는데, 웬걸… 이 과목은 사실상 수학과 과목 이었습니다.. ㅋㅋ 그래도 수학과 복수전공도 하고 있으니, 이 수업도 힘내서 잘 들어봅시다! 전체 포스트는 “미시경제학” 카테고리에서 확인하실 수 있습니다.

들어가며

번들과 번들 선호에 대해 살펴보고, 번들에 대한 선호가 가질 수 있는 특징에 대해서 살펴보고 있습니다.

• Monotonicity
• Continuity
• Convexity
• Differentiability

이번 포스트에선 번들 선호의 오목성(Convexity)에 대해서 살펴봅니다.

On the Linear Space

다섯명의 정치 후보 A, B, C, D, E가 있습니다. 곧 대선후보 경선인데 ㅋㅋ 이들이 좌/우 스펙트럼 상에 아래와 같이 정렬 되어 있습니다.

\[\rightarrow D \rightarrow A \rightarrow C \rightarrow B \rightarrow E\]

어떤 사람이 “자신은 후보의 정치적인 위치”만 고려하며, 후보 $A$보다 후보 $B$를 더 선호한다고 말했습니다.

이 정보를 바탕으로 한다면, 그 사람은 $C \succ B$라고 추론할 수 있습니다. 이유는 그 사람에 왼쪽 방향인 $B$에서 $A$ 이동하는게 개선이라면, 두 사람의 중간에 위치한 $C$로 이동하는 것도 더 선호할 것 입니다.

하지만, $A$와 $C$ 후보 사이에서는 선호를 판단할 수 없습니다. 이것은 추가적인 정보가 있어야 합니다.

또, 직선 상에서 $D$가 $A$보다 왼쪽에 있다고 해서, $D \succ A$라고 생각할 수는 없습니다. 우리는 $A$와 $B$ 사이의 선호에 대해서만 추론할 수 있습니다.

그러나, $B \succ E$는 추론할 수 있습니다. 그 이유는 후보 $E$는 후보 $B$보다도 $A$에게 멀리 떨어져 있기 때문입니다.

이것은 $A \succ B$라는 선호가 주어졌을 때, $A$에게 가까워지는 방향인지(후보 $C$), 아니면 $A$에게 멀어지는 방향인지(후보 $D$)를 기준으로만 선호를 추론할 수 있음을 말합니다.

후보 $D$의 경우도, $A \succ D$도 가능할 수 있는게, $A$가 선호 중심 $\mathbf{x}^\ast$라고 한다면, $A$가 항상 선호되는 후보이기 때문입니다.

Definition

For every $a \sim b$ and $a \ne b$, and for every $\lambda \in [0, 1]$,

\[\begin{gather*} \lambda a + (1 - \lambda) b \, \succcurlyeq \, a \\ \text{and} \\ \lambda a + (1 - \lambda) b \, \succcurlyeq \, b \end{gather*}\]

같은 무차별 곡선 위에 있는 $a$와 $b$ 사이의 어떤 “중간 지점”도 $a$와 $b$보다 선호된다는 성질 입니다.

$\lambda \in (0, 1)$로 $a$와 $b$ 사이의 선형 결합을 하는데, 이는 2차원 번들 평면 상에서 $a$와 $b$를 연결하는 선분의 임의의 점을 의미합니다. (기하학적 해석)

[Youtube] 미시경제학 (Microeconomics) Week 2-1: Indifference Curves and MRS

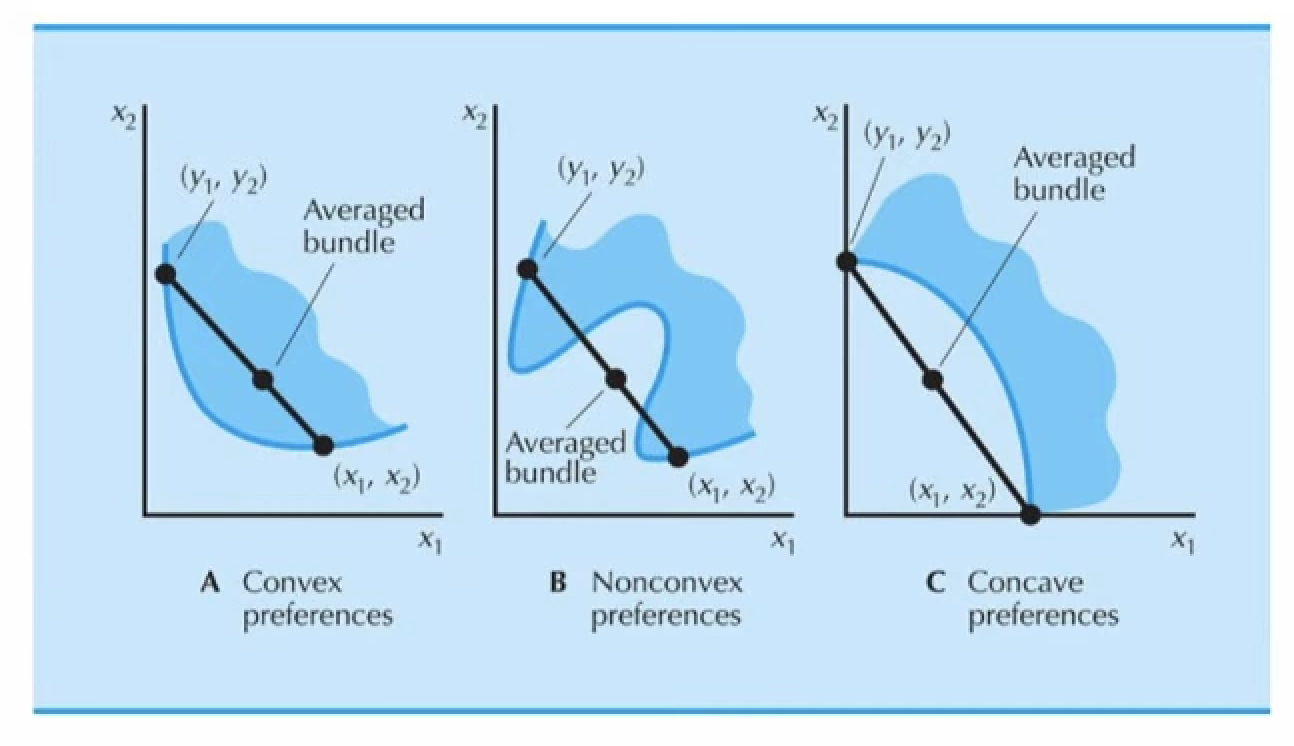
위의 그림은 번들 선호 그래프가 가질 수 있는 3가지 경우 입니다.

Strictly Convex

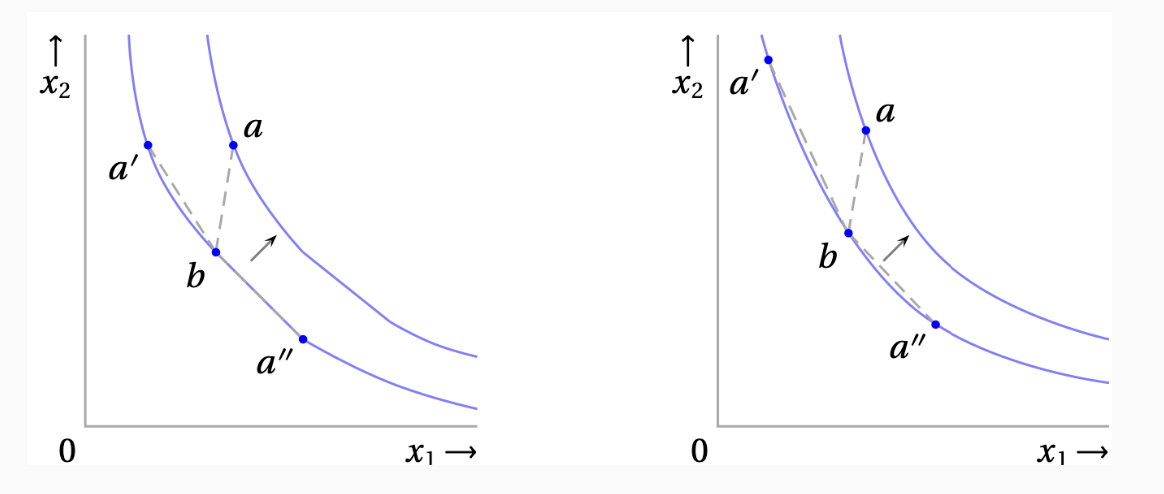
그래프에서 왼쪽은 “볼록한 선호”를 표현하고, 오른쪽은 “엄밀히 볼록한 선호”를 표현합니다.

차이는 선호 부등식에서 등호의 여부 입니다. “strictly convex”에서는 $\succ$로만 표현 합니다.

\[\begin{gather*} \lambda a + (1 - \lambda) b \, {\color{red} \succ} \, a \\ \text{and} \\ \lambda a + (1 - \lambda) b \, {\color{red} \succ} \, b \end{gather*}\]

Lexicographic preference

Lexicographic preferences are convex.

Assume $(a_1, a_2) \succ (b_1, b_2)$.

If $a_1 > b_1$, then for every $\lambda \in (0, 1)$, we have $\lambda a_1 + (1 - \lambda) b_1 > b_1$, and thus

\[\lambda a + (1 - \lambda) b \succ b\]

---

If $a_1 = b_1$, then $\lambda a_1 + (1 - \lambda) b_1 = b_1 = a_1$. In this case, we can do same thing on $a_2$ and $b_2$.

If $a_2 \ge b_2$, and hence $\lambda _2 + (1 - \lambda) b_2 \ge b_2$, so that $\lambda a + (1 - \lambda) b \succcurlyeq b$.

Properties

Upper Contour Set is Convex

어떤 소비 묶음 $x^\ast$가 주어졌을 때, 이것보다 선호되거나 무차별한 소비 묶음의 집합을 생각할 수 있습니다. 이것을 “상위선호 집합(Upper Contour Set)”라고 합니다.

\[\left\{x \in X: x\succcurlyeq x^\ast\right\}\]

The bundle preference is “convex” if and only if

for all $x^\ast \in X$, its “upper contour set” is convex.

상위선호 집합이 “볼록”하다는 것은 무슨 의미일까요? 이것은 집합의 볼록성에서 유래한 것인데,

그 집합 안에서 임의의 두 소비 묶음을 고르면, 그 둘 사이의 선형결합도 반드시 그 집합 안에 포함된다

라는 성질 입니다.

이것을 좀더 풀어서 얘기하면, 소비자가 $a$와 $b$ 상품 둘다 더 좋은 묶음이라고 판단했다면, 그 둘을 섞은 소비 묶음도 더 좋은 것이라고 판단다는 성질 입니다.

TODO… 일단은 스킵…

Utility Function is concave

효용 함수 $u(x)$가 오목(concave, convex가 아닙니다!)하다는 것은 “접선이 함수 위에 있는” 경우 입니다.

이것은 임의의 $a, b \in \mathbb{R}$에 대해 아래 부등식이 성립함을 말합니다.

\[u(\lambda a + (1 - \lambda)b) \ge \lambda u(a) + (1 - \lambda) u(b)\]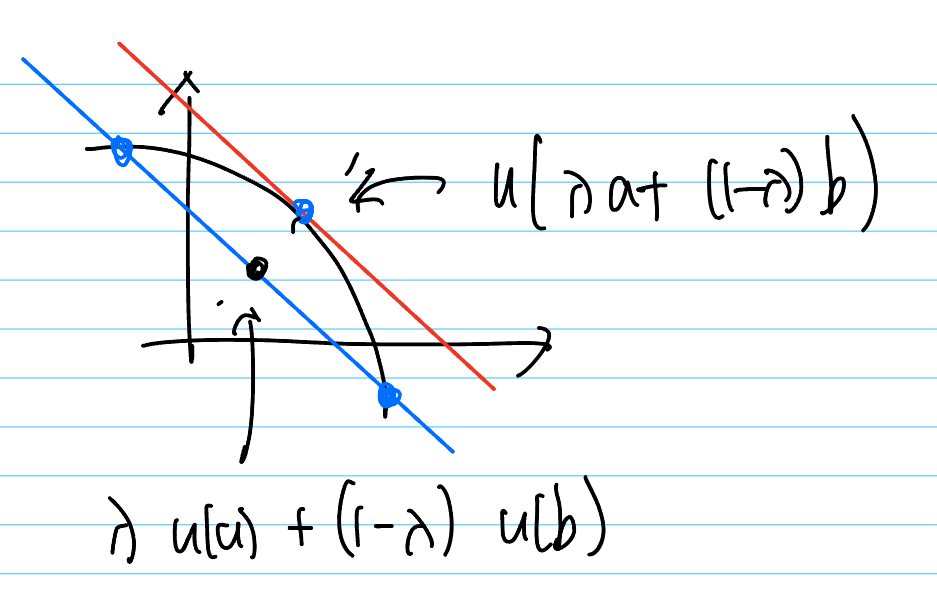

이것은 중간점의 함수값이, 함수의 기댓값보다 크다는 것을 말합니다. 즉, 이 둘을 섞은 선택이 (가중) 평균보다 더 좋거나 같다는 것을 말합니다.

Let $\succcurlyeq$ be a preference relation that is represented by a concave function $u(x)$.

Assume that $a \succcurlyeq b$, so that $u(a) \ge u(b)$.

By the concavity of $u(x)$,

\[u(\lambda a + (1-\lambda) b) \ge \lambda u(a) + (1-\lambda) u(b)\]

For right-side, due to $u(a) \ge u(b)$,

\[\lambda u(a) + (1-\lambda) u(b) = u(b) + \lambda (u(a) - u(b)) \ge u(b)\]

So,

\[u(\lambda a + (1-\lambda) b) \ge \lambda u(a) + (1-\lambda) u(b) \ge u(b)\]

Thus, $\lambda a + (1 - \lambda) b \succcurlyeq b$, so that $\succcurlyeq$ is convex.

그러나 이것의 역은 성립하지 않습니다! 왜냐하면, Convex preference 이지만, utility function이 non-concave인 경우가 있기 때문 입니다!

(ex) the convex preference represented by the concave function $\min(x_1, x_2)$ Also, by the function $(\min(x_1, x_2))^2$ is non-concave, but the preference is convex.

Convexity, strong monotonicity, and decreasing MRS

강한 단조성과 convexity를 가진 번들 선호는 감소하는 MRS 특성을 갖는다.

TODO… 증명이랑 예시도 있는데 와닿지 x…

Summary

[Youtube] 미시경제학 (Microeconomics) Week 2-1: Indifference Curves and MRS

보조 자료로 같이 보고 있는 유튜브 강좌에서 지금까지의 번들 선호를 이렇게 요약하고 있습니다.

맺음말

이제 나머지 번들 선호의 성질들도 살펴봅시다!

• Monotonicity
• Continuity
• Differentiability