Bundle Preference: Differentiability

졸업을 위해 마지막 학기에 “미시경제학” 수업을 듣게 되었습니다. 경제학원론 수업을 재밌게 들어서 경제 쪽이랑 궁합이 좋은 줄 알고 신청 했는데, 웬걸… 이 과목은 사실상 수학과 과목 이었습니다.. ㅋㅋ 그래도 수학과 복수전공도 하고 있으니, 이 수업도 힘내서 잘 들어봅시다! 전체 포스트는 “미시경제학” 카테고리에서 확인하실 수 있습니다.

들어가며

번들과 번들 선호에 대해 살펴보고, 번들에 대한 선호가 가질 수 있는 특징에 대해서 살펴보고 있습니다.

• Monotonicity
• Continuity
• Convexity
• Differentiability

이번 포스트에선 마지막 특성인 번들 선호의 “미분가능성(Differentiability)”에 대해서 살펴봅니다.

Smooth Indifference Curve

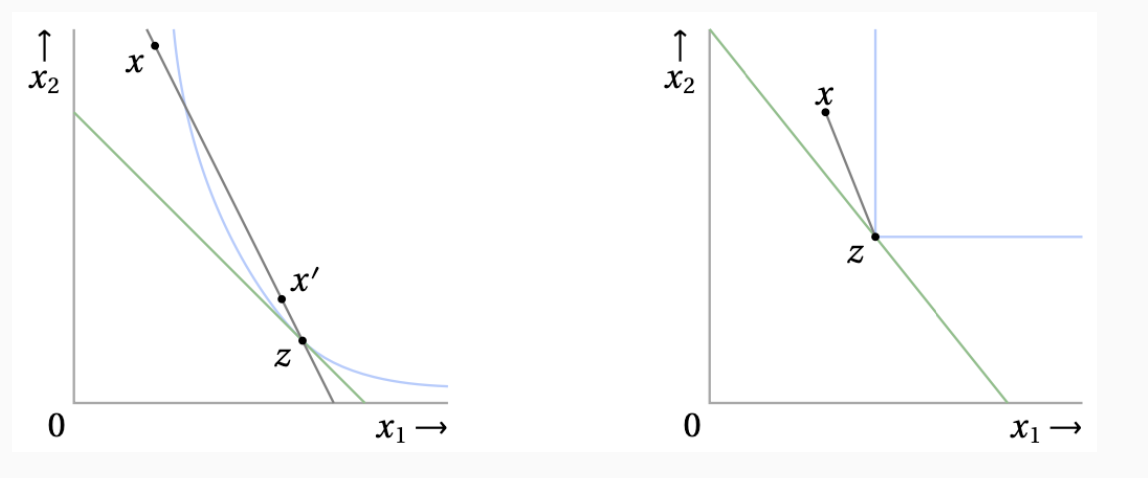
왼쪽 그래프는 Smooth 무차별 곡선 입니다. 점 $z$를 기준으로 뾰족한 부분 없이 부드럽게 연결 되어 있고, 점 $z$를 기준으로 접선을 그릴 수도 있습니다.

오른쪽 그래프는 non-smooth 무차별 곡선 입니다. 점 $z$를 기준으로 뾰족한 부분이 있고, 이로 인해 MRS가 불연속적이거나 정의되지 않을 수 있습니다.

Marginal Rate of Substitution

“한계 대체율(MRS)”는 소비자가 한 재화를 포기할 때, 다른 재화를 얼마나 더 가져야 같은 효용 수준을 유지할 수 있는지를 나타내는 비율 입니다.

수식으로 적으면 아래와 같습니다.

\[\text{MRS}_{xy} = - \frac{dy}{dx}\]

$dx$는 $x$ 재화를 아주 조금 더 소비하는 것을 말하고, $dy$는 이때, 소비자가 같은 효용을 유지하기 위해 줄여야 할 $y$ 재화의 양을 말합니다.

MRS는 “무차별 곡선”의 기울기와도 같습니다. 그러나, 곡선의 기울기가 각 점마다 다르듯이 MRS는 고정값이 아닙니다. (물론 곡선이 아니라 직선이라면 MRS가 고정값 입니다.) 이렇게 하나의 무차별 곡선 위에서도 MRS 값이 달라지는 것을 바탕으로 소비자가 현재 보유하는 재화의 양에 따라서 교환 비율인 MRS가 달라진다고 해석할 수 있습니다.

예를 들어, $x$ 재화는 엄청 많이 가지고 있는데, $y$ 재화는 하나도 없는 경우를 생각해봅니다. 그러면 그 사람은 $y$ 재화를 얻기 위해 $x$ 재화는 좀 크게 내놓을 의향이 있을 것 같습니다.

그리고 이런 MRS 경향을 가진 소비자는 무차별 곡선이 오목한 형태를 갖습니다. 그리고 경제학에서는 사람들의 무차별 곡선이 이런 오목한 형태를 가진다는 것을 가정 합니다.

반대로 무차별 곡선이 원점이 볼록한 형태라면, 이것은 비정상적이고 극단적인 선택 성향을 가진 사람 입니다. 이 사람은 한 재화가 적으면 적을수록 그 재화를 덜 중요하게 생각 합니다. 그리고 그 재화를 대체할수록 더 대체하고 없애버리고 싶어 합니다.

이런 극단적인 경향을 가진 사람은 오히려 한 재화만을 극단적으로 소비하려는 경향이 있습니다. 그래서 $x$ 재화만 전부 갖거나 $y$ 재화만 전부 갖는 상황을 혼합해서 가지고 있는 것보다 더 선호 합니다.

Marginal Utility

바로 정의로 들어가니까 너무 헷갈리더라구요… 일단 선행 개념을 먼저 다지고 들어가봅시다.

어떤 번들 $z = (z_1, z_2)$에 대해서 효용 함수 $u(z)$와 그 값은 소비자가 그 번들 $z$를 얼마나 좋아하는지 스칼라 값으로 표현한 것 입니다. 이것은 그 번들의 종합 효용 입니다.

이 스칼라 함수 $u(z)$를 $z_1$, $z_2$에 대해 편미분 하면, $z$ 위치에서 각 재화를 조금 늘렸을 때 효용이 얼마나 증가하는지를 알 수 있습니다. 이것을 “Marginal Utility”라고 합니다. 좀더 쉽게 이름 붙이면, “한계 효용”이라고 합니다. (수업 자료에서는 “Local Valuation”라고 표현 합니다만 저는 유튜브 강좌의 표현이 더 와닿는 것 같습니다!)

\[\begin{aligned} MU_1(z) &= \frac{\partial u}{\partial z_1}(z) \\ MU_2(z) &= \frac{\partial u}{\partial z_2}(z) \end{aligned}\]

이 편미분 값은 $z$ 근처에서 방향을 조금 바꿨을 때, 그 방향이 효용에 + 영향을 주는지 - 영향을 주는지, 그리고 얼만큼 영향을 주는지에 대해 판단하는 기준이 될 수 있습니다.

만약, 주어진 번들 $z$에 대해서 편미분 값인 $(MU_1(z), MU_2(z)) = (0, 0)$라고 한다면, 효용이 포화된 지점이라고 할 수 있습니다. 어느 지점으로 이동해도 효용이 변할 수 없는 지점 입니다. 이런 지점은 아주아주 예외적인 경우로 현실적으로 존재할 수 없고, 경제학에서도 예외적인 케이스로 분류합니다. 뒤에 이어지는 내용에서도 이것에 대해서는 제외하고 정의 합니다.

MRS vs. Marginal Utility

또 헷갈렸던 것은 MRS와 한계효용 입니다. MRS는 두 재화의 교환비 입니다. 반면에, 한계 효용은 다른 재화와 상관 없이 어떤 재화를 아주 조금 늘릴 때의 효용의 변화량 입니다. MRS는 효용을 유지하면서 교환하는 비율이라는 점도 명심 합니다.

한계 효용(MU) 하나만 가지고는 이 재화의 가치나 교환비를 알 수 없습니다. 그래서 아무 의미가 없습니다. 한계 효용 값은 같은 지점에서 $MU_1$, $MU_2$를 알고 이것을 나누어 비율을 내야 그제서야 “한계 교환비(MRS)”라는 의미를 갖게 됩니다!!

그래서 한계 효용를 사용해 MRS를 아래와 같이 정의 합니다.

\[\text{MRS} = \frac{\partial u(z) / \partial z_1}{\partial u(z) / \partial z_2}\]

Non-differentiable bundle preference: Kinky Preference

아직 정의를 살펴보지도 않았는데 ㅋㅋ 미분불가능한 번들 선호의 사례들부터 먼저 살펴봅시다.

[Youtube] 미시경제학 (Microeconomics) Week 2-4: Consumer choice

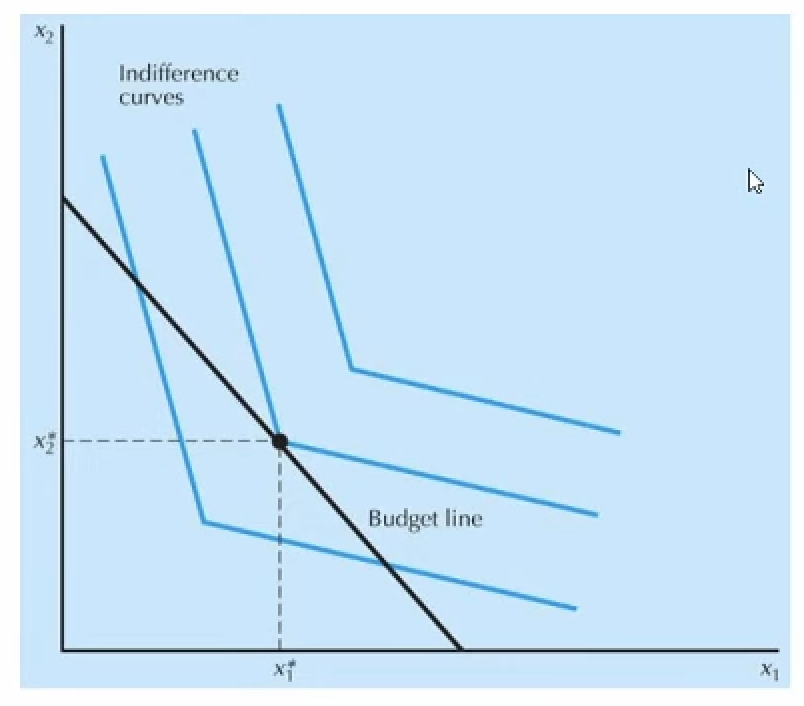
그림의 곡선은 아래의 Utility Function을 갖는 번들 선호 입니다.

\[u(x_1, x_2) = \min \left\{ 2x_1 + x_2, x_1 + 2 x_2 \right\}\]

이 선호는 “non-strictly convex” 입니다. 기울기가 strictly decreasing 하지 않습니다.

또, 이 선호는 미분불가능 번들 선호 입니다. 꺽이는 지점에서 한계 효용(MU)으로 그리는 접선이 하나로 일치하지 않습니다.

사실 이것 왜에도 “Perfect Complements”나 “꺽인 점”이 있는, 불연속점이 있는 다른 모든 번들 선호는 모두 미분불가능 성질을 갖습니다.

Differentiable Bundle Preference

좋았어! 이제 정의를 살펴봅시다!

A monotone and convex preference relation $\succcurlyeq$ is “differentiable”,

if for every bundle $z$,

there is $(v_1(z), v_2(z)) \ne (0, 0)$ of non-negative numbers
(called the consumer’s local valuations at $z$),

then for all numbers $\delta_1$ and $\delta_2$,

\[\begin{gather*} v_1(z) \delta_1 + v_2(z) \delta _2 > 0 \\ \iff \\ \exists \quad \epsilon > 0 \quad \text{s.t.} \quad z + (\epsilon \delta_1, \epsilon \delta_2) \succ z \end{gather*}\]

이 파트를 공부하면서 헷갈린게, “무차별 곡선이 미분가능”이라고 생각했던 것 입니다. 미분가능성은 “번들 선호”에 대해 정의하는 것 입니다. 무차별곡선은 전체 선호체계의 한 단면에 불과합니다. 그래서 무차별 곡선에 대해서는 매끄럽고 미분 가능하더라도 전체 선호 체계가 불연속적이거나 모순적일 수 있습니다.

local valuation $v_1(z), v_2(z)$는 각각의 재화를 조금 더 가질 때, 소비자가 느끼는 좋아지는 정도를 표현한 값 입니다. $(\delta_1, \delta_2)$는 방향 벡터 입니다. 지금 $z$에서 어떤 방향으로 움직이려고 하는지 표현하는 벡터 입니다.

$v_1(z) \delta_1 + v_2(z) \delta_2$는 그 방향으로 갔을 때, 효용이 얼만큼 증/감 하는지 표현한 값 입니다. 그리고 이게 증가하는 상황이라면 $\ast > 0$ 이 방향은 소비자에게 더 나은 방향이라는 것 입니다.

그러면, 아주 조금만 $\epsilon$ 만큼만 움직여도 그 선호 변화가 실제로 느껴진다는 것을 말합니다. 그 결과가

\[z + (\epsilon \delta_1, \epsilon \delta_2) \succ z\]

로 표현된 것 입니다.

참고로 $z + (\epsilon \delta_1, \epsilon \delta_2)$ 이 표현은 미적분학에서 스칼라 함수 $u(z)$에서 $z$에 접하는 접평면을 정의하는 방법 입니다. 접평면 위의 점이 접점의 효용보다 더 크다면, 당연히 선호되겠죠? 이 접면이 정의되고, 그게 번들 선호로 이어진다는 걸로 미분가능성을 정의하는 흐름인 것 같습니다.

(주저리 주저리 적었지만 아직 확 와닿지는 않네요..;;)

Lexicographic preferences are not differentiable

사전식 선호에서 소비자는 첫번째 재화의 양을 “절대적”으로 우선시 합니다. 그래서 사전식 선호에서 소비자가 선호를 느끼는 유일한 방법은 첫번째 재화를 늘리는 방향 밖게 없습니다.

그 외의 모든 방향은 선호에 영향을 미칠 수도 있고, 아닐 수도 있습니다. 예측 불가능 하죠.

그래서 $(1, 0)$ 방향만이 유일하고 명확하게 더 좋아지는 방향입니다.

$(0, 1)$ 방향으로 움직인다고 해봅시다. 첫번째 재화는 그대로이고, 두번째 재화만 늘어납니다. 한계 효용은 $v_1(z) = 1$, $v_2(z) = 0$로 정의해봅시다. 그러면 $v_1(z) \delta_1 + v_2(z) \delta_2 = 0$이 됩니다.

그런데, 만약 $z_1$ 값이 고정되어 있다면, $z_2$이 커지는 방향 $(0, 1)$으로 이동하면 선호는 더 나아집니다. 그래서 실제로는 $z + \epsilon(0, 1) \succ z$ 입니다. 그러나 $\ast = 0$이기 때문에, 미분가능성의 조건을 만족 하지 않습니다!!

(미분가능성의 정의는 양쪽을 모두 만족해야 합니다.)

Differentiable when Smooth Utility

번들 선호의 미분가능성을 어렵게 구할 필요 없이, 번들 선호를 정의하는 효용 함수를 알고 있다면, 그걸로 번들 미분가능성을 유도할 수 있습니다.

증명은 스킵!

Summary

[Youtube] 미시경제학 (Microeconomics) Week 2-1: Indifference Curves and MRS