Introduction: Numerical Differentiation

수학과 복수전공을 위해 졸업 마지막 학기에 “수치해석개론” 수업을 듣게 되었습니다. 수학과 졸업시험도 겸사겸사 준비할 겸 화이팅 해봅시다!! 전체 포스트는 “Numerical Analysis“에서 확인할 수 있습니다.

들어가며

지금까지 함수 $f(x)$를 매끄러운 함수로 보간하는 방법에 대해 다뤘고, 이렇게 보간한 함수로 도함수 $f’(x)$를 근사하는 것도 살펴보았습니다.

이번 포스트부터 보간 기반이 아닌 다른 방식으로 접근하게 됩니다! 그리고 도함수 $f’(x)$에 대한 다른 근사 방법인 “뉴턴-코츠 방식”에 대해 살펴봅니다.

Forward, Backward Difference

본래 함수의 도함수는 아래와 같이 극한을 사용해 정의 합니다.

\[f'(x) = \lim_{h\rightarrow 0} \frac{f(x+h) - f(x)}{h}\]

그런데, 수치적 접근에서는 $h \rightarrow 0$ 같은 걸 할 수 없으니, 적당한 미소값 $h$를 잡은 후 아래와 같이 미분 근사값을 구합니다.

\[D_+ f(x) = \frac{f(x+h) - f(x)}{h}\]

그리고 이것을 “전방 차분(Forward Difference)”라고 부릅니다. 반대로 이전 값을 사용할 수도 있습니다.

\[D_{-} f(x) = \frac{f(x) - f(x-h)}{h}\]

이것을 “후방 차분(Backward Difference)”라고 부릅니다. 전방 차분과 후방 차분은 한쪽에 대한 근사 입니다: one-sided approximation of $f’(x)$.

1st order Accuracy

$D_{+}f(x)$와 $D_{-}f(x)$ 모두 “1차 정확도”를 가지는 근사법 입니다. 이것은 실제 미분값과 전방/후방 차분으로 근사한 값의 오차가 $h$에 비례하는 $O(h)$로 정의된다는 것을 말합니다.

이것은 $h$ 값을 작게 할수록 실제값과의 차이가 선형으로 감소한다는 것을 말합니다.

Centered Difference

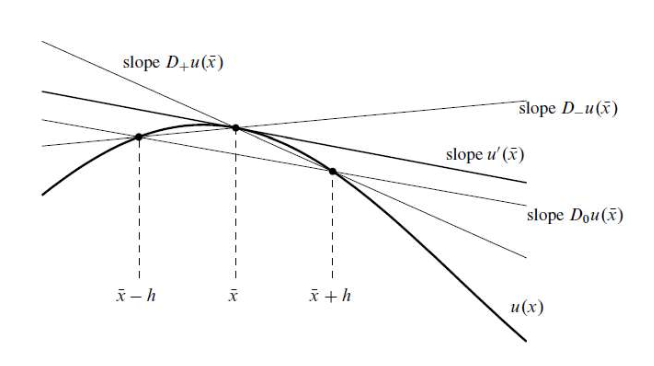
요렇게 볼록점에서의 미분값을 근사한다고 하면, 전방 차분과 후방 차분은 그리 좋은 값을 제시하지 못 합니다. 그래서 등장한 것이 이 둘의 평균값을 사용하는 중앙 차분 입니다.

\[D_0 f(x) = \frac{f(x+h) - f(x-h)}{2h} = \frac{D_{+}f(x) - D_{-}f(x)}{2}\]

위 그림에서 볼 수 있듯이 중앙 차분 $D_0 f(x)$가 한쪽만 보는 차분보다는 더 좋은 근사를 보여주는 걸 알 수 있습니다.

그리고 중앙 차분은 “2차 정확도”를 제공 합니다. 이것은 실제값과의 오차가 $h^2$에 비례한다는 것으로 $O(h^2)$라고 표현 합니다.

Higher-order Accuracy

중앙 차분보다 더 높은 정확도를 갖도록 하는 것도 가능 합니다.

\[D_3 f(x) = \frac{2f(x+h) + 3f(x) - 6 f(x-h) + f(x-2h)}{6h}\]

라고 차분을 정의합니다. 이 차분은 $x-2h, x-h, x, x+h$ 4개 점을 활용해 차분을 구합니다. 이 차분은 “3차 정확도”를 제공 합니다: $O(h^3)$.

위와 같은 공식을 유도하는 시스템이 “뉴턴-코츠 방식”입니다. 앞으로 이어지는 내용에서 이 방식에 대해 살펴볼 예정 입니다.

log-log scale

… 스킵!

Truncation Error

$f(x+h)$와 $f(x-h)$를 테일러 전개 해봅시다.

\[\begin{aligned} f(x+h) &= f(x) + hf'(x) + \frac{1}{2}h^2 f''(x) + \frac{1}{6}h^3 f'''(x) + O(h^4) \\ f(x+h) &= f(x) - hf'(x) + \frac{1}{2}h^2 f''(x) - \frac{1}{6}h^3 f'''(x) + O(h^4) \end{aligned}\]

그리고 이걸 전방/후방 차분의 공식에 대입해보면…

\[D_{+} f(x) = \frac{f(x+h) - f(x)}{h} = f'(x) + \frac{1}{2}h f''(x) + \frac{1}{6} h^2 f'''(x) + O(h^3)\]

전방 차분은 $f’(x)$는 정확히 나온 것이고, 그 다음 오차항은 $\frac{h}{2} f’‘(x)$ 크기로 나옵니다. 그래서 전방 차분의 오차는 $O(h)$가 됩니다. 후방 차분의 오차도 마찬가지로 $O(h)$로 나옵니다.

중앙 차분에 대해서도 구해봅시다. 중앙 차분은 전방/후방 차분을 더한 것의 평균으로 구할 수 있습니다.

\[D_0 f(x) = \frac{D_{+}f(x) + D_{-}f(x)}{2} = f'(x) + \frac{1}{6} h^2 f'''(x) + O(h^4)\]

그래서 중앙 차분에서는 오차가 $O(h^2)$의 정확도를 갖게 됩니다.

마지막으로 $D_3 f(x)$에 대해서도 수행해봅시다. $D_3$를 구하기 위해선 $f(x-2h)$의 테일러 전개가 필요 합니다.

\[f(x - 2h) = f(x) - 2h f'(x) + \frac{1}{2}(2h)^2 f''(x) - \frac{1}{6}(2h)^3 f'''(x) + O(h^4)\]

이걸 $D_3 f(x)$의 공식에 따라 조합하고 정리하면 아래와 같이 됩니다.

\[D_3 f(x) = f'(x) + \frac{1}{12} h^3 f^{(4)} (x) + O(h^4)\]

따라서, 3차 정확도가 $O(h^3)$가 됩니다.

Rounding Error

수치 미분은 $h$ 값에 따라 오차가 작아집니다. 그러나 단순히 $h$를 무조건 작게 만든다고 좋은 것은 아닙니다!

$h$가 너무 작아지면, “반올림 오차(round-off error)”가 커져서 오히려 결과가 나빠질 수도 있습니다.