[NA] Before Midterm

수학과 복수전공을 위해 졸업 마지막 학기에 “수치해석개론” 수업을 듣게 되었습니다. 수학과 졸업시험도 겸사겸사 준비할 겸 화이팅 해봅시다!! 전체 포스트는 “Numerical Analysis“에서 확인할 수 있습니다.

Generalized Mean Value Theorem

연속성을 갖고 $(n-1)$번 미분 가능한 나이스한 함수 $f(x)$가 있습니다. 이 함수는 구간 $[a, b]$ 내의 $n$개 점 $\left\{ x_i \right\}$에 대해 함수값이 0 입니다.

\[f(x_i) = 0\]

이때, 아래의 어떤 실수 $\xi \in (a, b)$가 있어서 아래 식을 만족함을 보여라.

\[f^{(n-1)} (\xi) = 0\]

Proof

(어떤 보간법에 대해서 증명할 때, 썼던 테크닉 같은데 어떤 보간법인지 기억이 안 나네요.. ^^;;)

사실 풀이는 Mean Value Theorem을 반복해서 적용하면 됩니다! 단순하죠? ㅋㅋ 그림으로 그리면 아래와 같은 과정을 반복해서 $f^{(n-1)}(\xi) = 0$를 찾는다고 보면 됩니다.

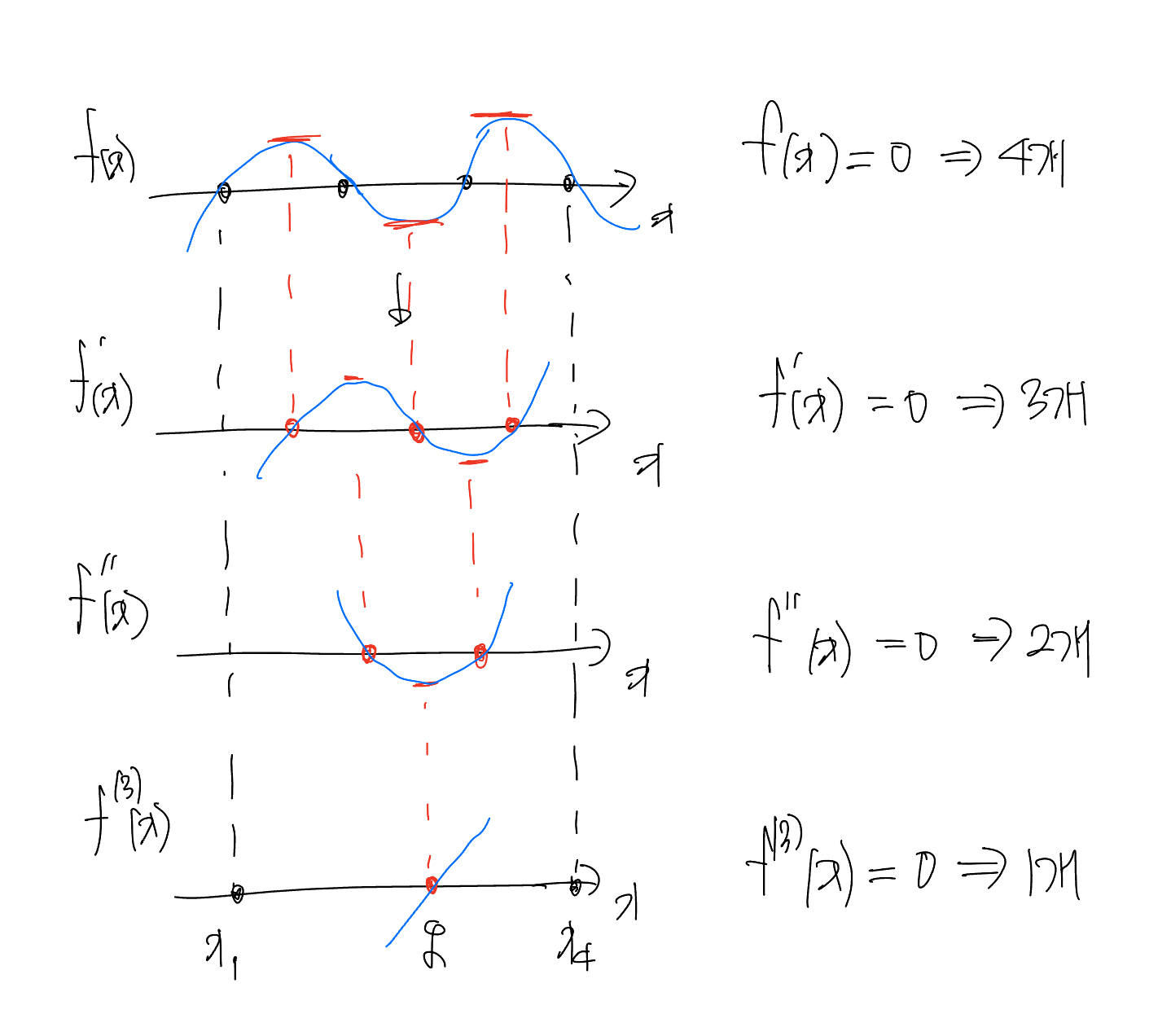
참고로 GMVT는 “Divided Difference”에 대한 Mean Value Theorem이라고도 볼 수 있습니다!