Numerical Integration

수학과 복수전공을 위해 졸업 마지막 학기에 “수치해석개론” 수업을 듣게 되었습니다. 수학과 졸업시험도 겸사겸사 준비할 겸 화이팅 해봅시다!! 전체 포스트는 “Numerical Analysis“에서 확인할 수 있습니다.

들어가며

수치적 적분은 우리가 함수 $f(x)$와 데이터 포인트 $(x_i, y_i)$들만 알고 있을 때, 이것들을 사용해 정적분 $\int f(x)$의 값을 근사하는 것 입니다.

이번 포스트에서는 주어진 함수 $f(x)$의 부정적분 $\int_a^b f(x)\,dx$를 수치적 적분으로 구하는 방법을 살펴봅니다. 수치적으로 부정적분은 아래와 같은 꼴을 갖게 됩니다.

\[\int_a^b f(x) \, dx = \sum_{i=0}^n a_i f(x_i)\]

이때, 데이터 포인트의 집합 $\left\{ x_0, \dots, x_n \right\}$은 $[a, b]$ 사이의 서로 다른 점들 입니다.

Trapezoid Rule

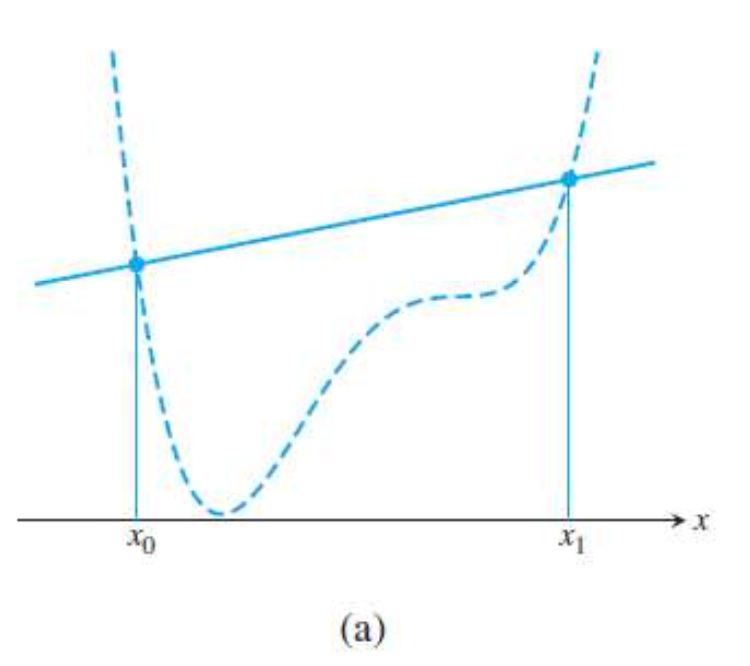
“Trapezoid”는 사다리꼴이라는 뜻 입니다. 이 방식은 데이터 포인트를 단 2개만 사용합니다.

그래서

• $x_0 = a$
• $x_1 = b$
• $h = (b-a)$

로 구성 됩니다. 그리고 이걸로 Langrange 보간 함수를 구하면

\[P(x) = \frac{(x-x_1)}{(x_0 - x_1)} f(x_0) + \frac{(x-x_0)}{(x_1 - x_0)} f(x_1)\]

이런 Linear Lagrange Polynomial이 나옵니다. 그리고 이걸 적분하면,

\[\int_a^b f(x) \, dx = \int_{x_0 = a}^{x_1 = b} \left[ \frac{(x-x_1)}{(x_0 - x_1)} f(x_0) + \frac{(x-x_0)}{(x_1 - x_0)} f(x_1) \right] \, dx + \text{Err Term}\]

에러 텀은 나중에 분석하고 일단 계속 작성해봅시다.

\[\begin{aligned} \int_a^b f(x) \, dx \approx &= \left[ \frac{(x-x_1)^2}{2(x_0 - x_1)} f(x_0) + \frac{(x-x_0)^2}{2(x_1 - x_0)} f(x_1) \right]_{x_0}^{x_1} \\ &= \frac{x_1 - x_0}{2} [f(x_0) + f(x_1)] \\ &= \frac{f(x_0) + f(x_1)}{2} h \end{aligned}\]

즉, 사다리꼴의 넓이로 수치적 적분을 구합니다! 정말 심플한 접근법!! ㅋㅋㅋ

Simpson’s Rule

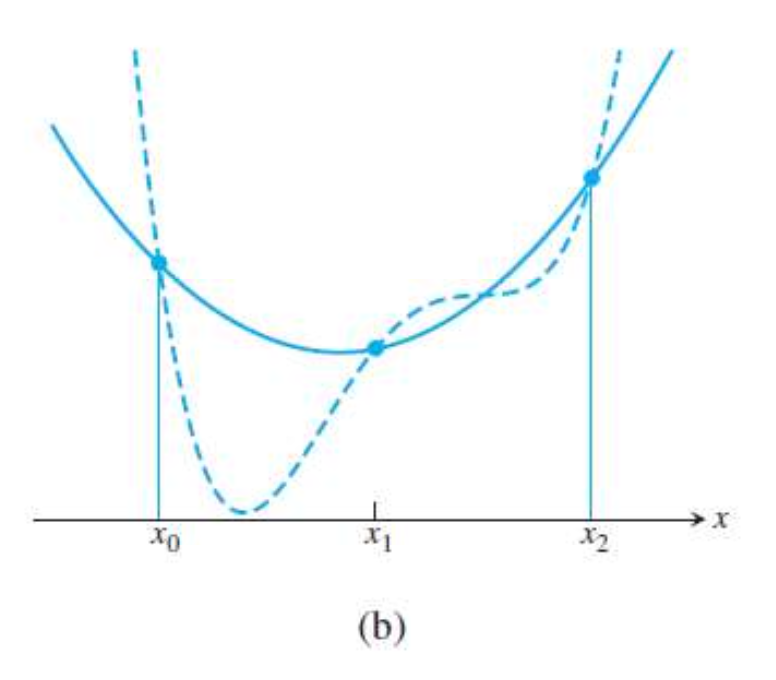
이번에는 균등하게 분포된 3개의 점을 사용해 적분 근사를 수행합니다.

• $x_0 = a$
• $x_1 = a + h$
• $x_2 = b$
• $h = (b-a)/2$

마찬가지로 라그랑주 근사를 합니다.

\[P_2(x) = \frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}f(x_0) + \frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)}f(x_1) + \frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}f(x_2)\]

이때, 각 $(x-x_i)(x-x_j)$에 대한 적분을 구해서 식을 정리하려고 하면… 지옥이 펼쳐집니다.. ㅋㅋ (직접 해봄;;)

결론부터 적으면, 심프슨 방식의 적분 근사는 아래와 같이 유도 됩니다.

\[\int_{x_0}^{x_2} f(x) \, dx \approx \frac{h}{3} (f(x_0) + 4 f(x_1) + f(x_2))\]

그래서 일반성을 잃지 않고(w.l.o.g), $x_1 = 0$를 설정하고, $x_0 = -h$, $x_1 = h$가 되는 수평 이동한 함수 $g(x)$에 대해서 적분 근사를 대신 수행합니다.

$P_2(x)$는 아래와 같이 다시 작성 됩니다.

\[P_2(x) = \frac{(x)(x-h)}{(-h)(-2h)}f(x_0) + \frac{(x+h)(x-h)}{(+h)(-h)}f(x_1) + \frac{(x+h)(x)}{(2h)(h)}f(x_2)\] \[\begin{aligned} \int_{-h}^{h} f(x) \, dx &\approx \int_{-h}^{h} P_2(x) \, dx \\ &= \int_{-h}^{h} \frac{1}{2h^2} \left[ x(x-h)f(x_0) - 2 (x^2 - h^2) f(x_1) + x(x+h) f(x_2) \right] \, dx \\ &= \int_{-h}^{h} \frac{1}{2h^2} \left[ x^2 f(x_0) - xhf(x_0) - 2x^2 f(x_1) + 2h^2 f(x_1) + x^2 f(x_2) + xh f(x_2) \right] \, dx \\ \end{aligned}\]

여기에서 기함수는 대칭성으로 인해 적분값이 0이 됩니다. 이것들을 버려내면

\[\begin{aligned} \int_{-h}^{h} f(x) \, dx &\approx \int_{-h}^{h} P_2(x) \, dx \\ &= \int_{-h}^{h} \frac{1}{2h^2} \left[ x^2 f(x_0) - 2x^2 f(x_1) + 2h^2 f(x_1) + x^2 f(x_2) \right] \, dx \\ \end{aligned}\]

그리고 실제로 적분을 수행해봅시다! 이 적분은 (비교적) 간단합니다!

\[\begin{aligned} \int_{-h}^{h} f(x) \, dx &\approx \int_{-h}^{h} P_2(x) \, dx \\ &= \frac{1}{2h^2} \left[ \frac{2}{3}h^3 f(x_0) - \frac{4}{3}h^3 f(x_1) + 4 h^3 f(x_1) + \frac{2}{3}h^3 f(x_2) \right] \\ &= \frac{h}{3} f(x_0) - \frac{2h}{3}f(x_1) + 2hf(x_1) + \frac{h}{3}f(x_2) \\ &= \frac{h}{3}\left[ f(x_0) + 4f(x_1) + f(x_2) \right] \end{aligned}\]

와우!! 심프슨 공식이 유도 되었습니다 ㅎㅎ 적분은 수평 이동한 함수에서 수행하든 원래 위치에서 수행하든 상관 없습니다! 그래서 이것 그대로 결과로 사용하면 됩니다!

4-points case

데이터 포인트가 2개, 3개로 늘어났는데, 4개인 경우는 어떻게 될까요? 이 경우도 공식이 있습니다.

이것은 “Simpson’s 3/8 Rule”라고 하며, 공식은 아래와 같습니다.

\[\int_{x_0}^{x_3} f(x) \, dx \approx \frac{3h}{8} (f(x_0) + 3f(x_1) + 3f(x_2) + f(x_3))\]

공식에 대한 유도는 3-point에서 했던 것처럼 함수를 평행이동 한 후에 수행해주면 된다고 합니다.

(Closed) Newton-Cotes Formula

지금까지 살펴본 Trapezoid Rule, Simpson’s Rule 모두 등간격 데이터 포인트에서의 적분 근사를 하는 방법이었습니다.

이것을 일반화 하여 $n$개 등간격 포인트에서 수행하는 것을 “뉴턴-코츠 공식“이라고 합니다.

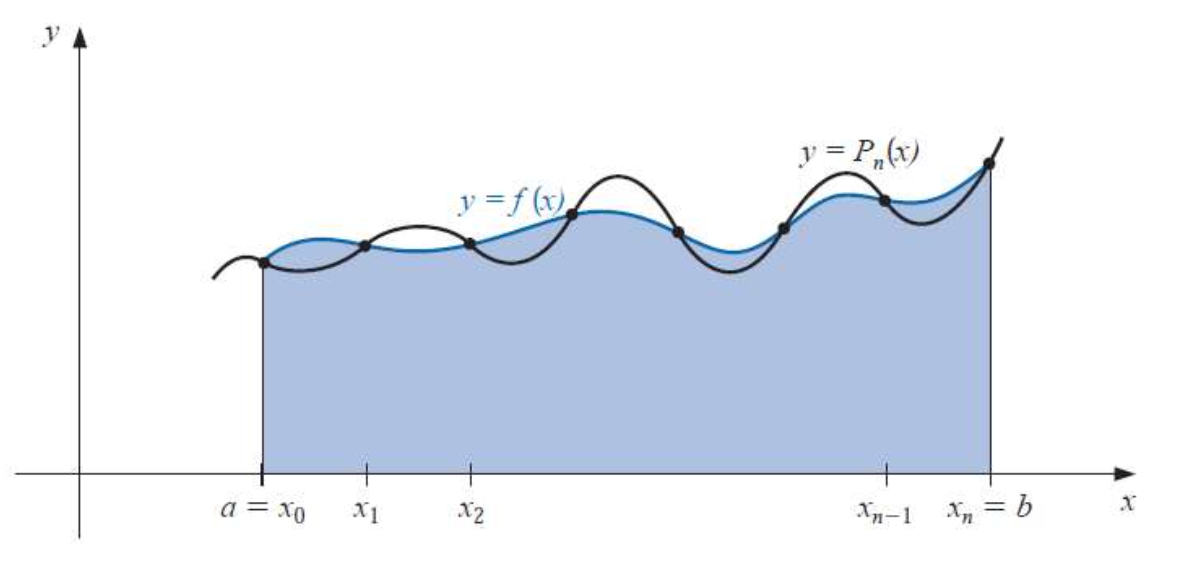
뉴턴-코츠 공식은 구간의 양 끝점을 포함하는지, 포함하지 않는지에 따라 “닫힌 공식”과 “열린 공식”으로 나뉩니다. 이번 포스트에서 살펴본 적분 근사들은 모두 “닫힌 뉴턴-코츠 공식” 입니다.

Degree of Precision

수치적분으로 정확히 적분이 가능한 다항식의 최고 차수를 말합니다.

예를 들어, 사다리꼴 법칙의 정확도는 $k=1$로 1차 다항식까지는 정확하게 수치 적분을 하지만, 2차 다항식에서는 오차가 발생 합니다. 심프슨 법칙의 정확도는 $k=2$로 2차 다항식까지는 정확하게 수치 적분을 제공 합니다.

Error Analysis

일단 스킵!

Trapezoid Rule

Simpson’s Rule

Closed Newton-Cotes formula

Open Newton-Cotes Formula

이번에는 구간 $[a, b]$의 양 끝점을 포함하지 않는 방식으로 수치 적분을 수행 합니다.

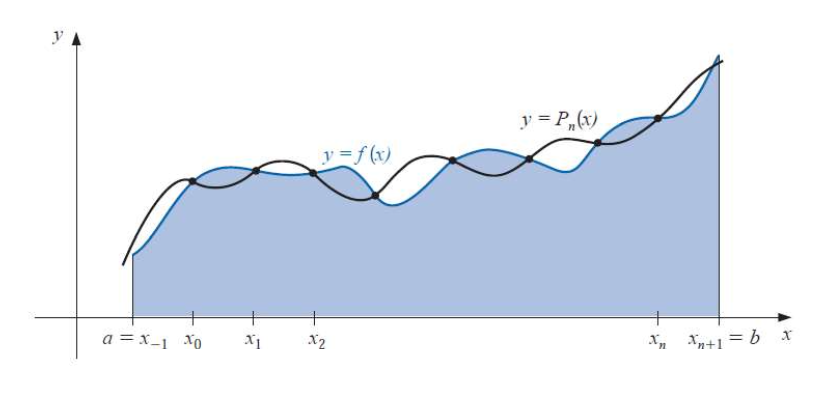
이때, 데이터 노드는 등간격으로 분포하지만, $[a, b]$ 양 끝점을 포함하지는 않습니다.

수업에서는 아래와 같이 데이터 노드는 레이블링 합니다.

• interval start $a = x_{-1}$
• interval end $b = x_{n+1}$
• start node $x_0 = a + h$
• end node $x_n = b - h$
• space $h = (b-a)/(n+2)$

그리고 열린 뉴턴-코츠의 식은 아래와 같이 작성 됩니다.

\[\int_{a}^{b} f(x) \, dx \approx \sum_{i=0}^n a_i f(x_i)\]

Closed Form vs. Open Form

Closed Form은 함수가 양 끝점을 모두 포함하는, 경계를 포함하는 방법 입니다. 반면에 Open Form은 함수의 양 끝점을 포함하지 않는데요. 이것은 $a, b$에서 불연속이 발생하거나 정의되지 않는 “특이점”일 때 Open Form을 사용해 수치 적분을 수행하게 됩니다.

반면에 둘의 공통점도 존재합니다! 둘다 데이터 노드의 갯수가 짝수 일 때, 홀수 일때보다 더 좋은 기대치를 제공합니다. 즉, $2n$일 때가 $2n-1$보다 더 좋은 Degree of Precision $k$를 제공하고, $2n$은 $2n+1$보다 같은 Deg of Precession $k$를 가집니다.

이 부분도 추후에 좀더 분석해보겠습니다.

Composite Newton-Cotes Formula

기존 접근은 구간을 $[a, b]$ 하나만 정의하고, 여기 위에서 수치 적분을 수행 했습니다. 하지만 이것은 복잡한 함수를 수치적분 하거나 긴 구간에 대해서는 정확도가 떨어지거나 오차가 커지는 문제가 있었습니다.

그래서 “합성 수치적분” 방법이 등장했습니다! 합성 수치적분은 단일 구간이 아니라 적분하려는 구간 $[a, b]$를 작은 하위 구간으로 나누고, 각 하위 구간에 기존 적분 공식을 독립적으로 적용 합니다!

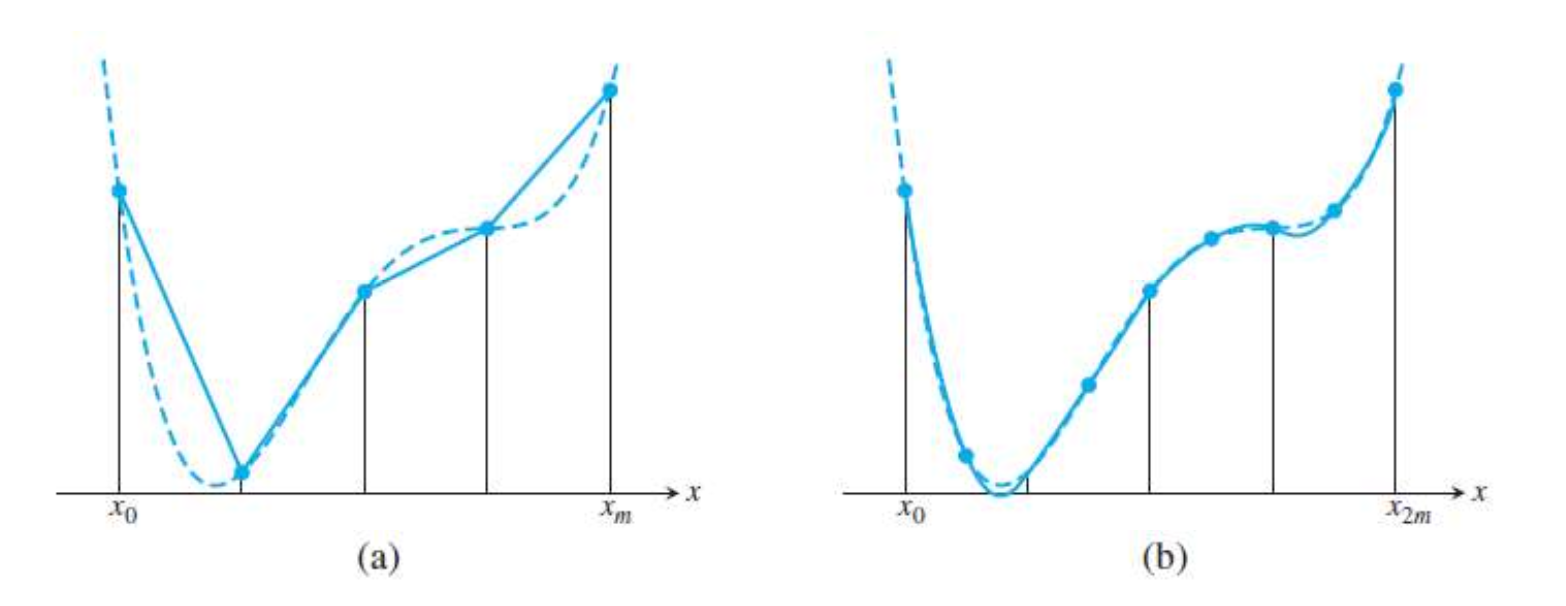
Composite Trapezoidal Rule

Composite Simpson Rule

맺음말

합성 뉴턴-코츠 방법은 이전에 살펴본 “스플라인(Spline) 보간법“과 접근이 비슷한 것 같습니다. 전체 구간에 대해 함수 근사를 하는게 아니라 하위 구간으로 나누어 지역적(locally) 접근하는 접근으로 오차나 진동(runge effect)를 해결하려고 하는 점이 같은 맥락인 것 같습니다.