Internal·Boundary Solution

졸업을 위해 마지막 학기에 “미시경제학” 수업을 듣게 되었습니다. 경제학원론 수업을 재밌게 들어서 경제 쪽이랑 궁합이 좋은 줄 알고 신청 했는데, 웬걸… 이 과목은 사실상 수학과 과목 이었습니다.. ㅋㅋ 그래도 수학과 복수전공도 하고 있으니, 이 수업도 힘내서 잘 들어봅시다! 전체 포스트는 “미시경제학” 카테고리에서 확인하실 수 있습니다.

들어가며

번들 선호에 대한 “미분가능성(differentiability)“에 대해 다루면서, 한계대체율(MRS)에 대해서도 살펴보았습니다.

MRS는 어려운게 아니고, 그냥 무차별 곡선에서의 기울기 였죠!! ㅎㅎ MRS는 해당 지점에서의 local valuation의 비율로 구성 됩니다. 이때, local valuation은 그냥 효용의 편미분값을 말합니다 ㅎㅎ

\[\text{MRS} = - \frac{v_1(x)}{v_2(x)} = \frac{MU_{x_1}}{MU_{x_2}}\]

그리고 MRS는 $x_1$을 한 단위 더 소비하기 위해, $x_2$를 얼만큼 “줄여야” 하는지를 수치적으로 표현합니다.

Optimal Solution and MRS

소비자가 주어진 예산 집합 안에서 최적해를 선택할 때, 그 위치에 따라서 MRS와의 관계가 달라집니다!

Internal Solution

만약 최적해 $x^{\ast}$가 $x_1^{\ast}, x_2^{\ast} > 0$라면, 아래의 등식이 성립 합니다.

\[\text{MRS}(x^{\ast}) = p_1 / p_2\]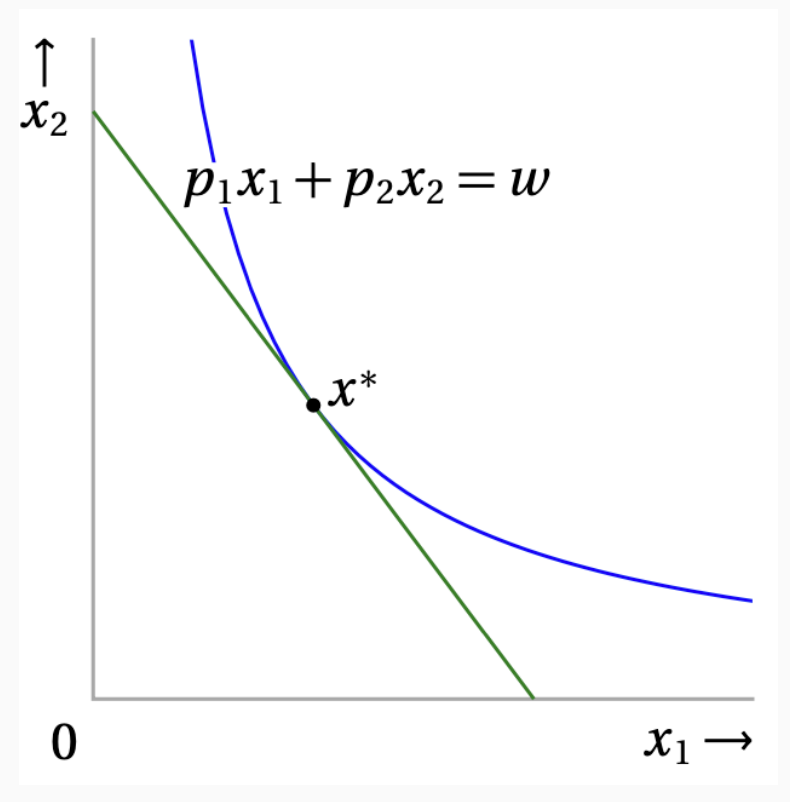

이것은 버짓 라인과 접하는 무차별 곡선 위에서 최적해가 발생한다고 해석할 수 있습니다.

Boundary Solution

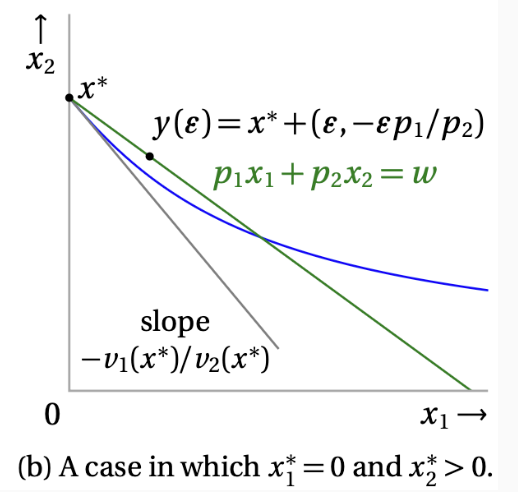
반면에 최적해가 경계인 $x_1^{\ast} = 0$ 또는 $x_2^{\ast} = 0$ 위에서 발생할 수 있습니다.

이 경우는 버짓 라인과 접하는 무차별 곡선이 존재하지 않기 때문에 이런 상황이 발생합니다.

이 경우, MRS와 교환비 사이에 부등식이 성립해도, 해의 최적성이 충족 됩니다.

\[\text{MRS}(x^{\ast}) < p_1 / p_2\]

Boundary Examples

처음에는 내부해의 예시가 더 쉬울거라고 생각했는데요! 공부를 해보니, 경계해의 예시를 찾는게 훨씬 쉽고 이해도 더 쉽습니다 ^^

Perfect Substitutes

효용 함수가 $u(x) = x_1 + x_2$로 주어졌습니다. 그리고 두 재화의 가격비는 $p_1:p_2 = 1:2$, 즉 재화1이 더 저렴합니다.

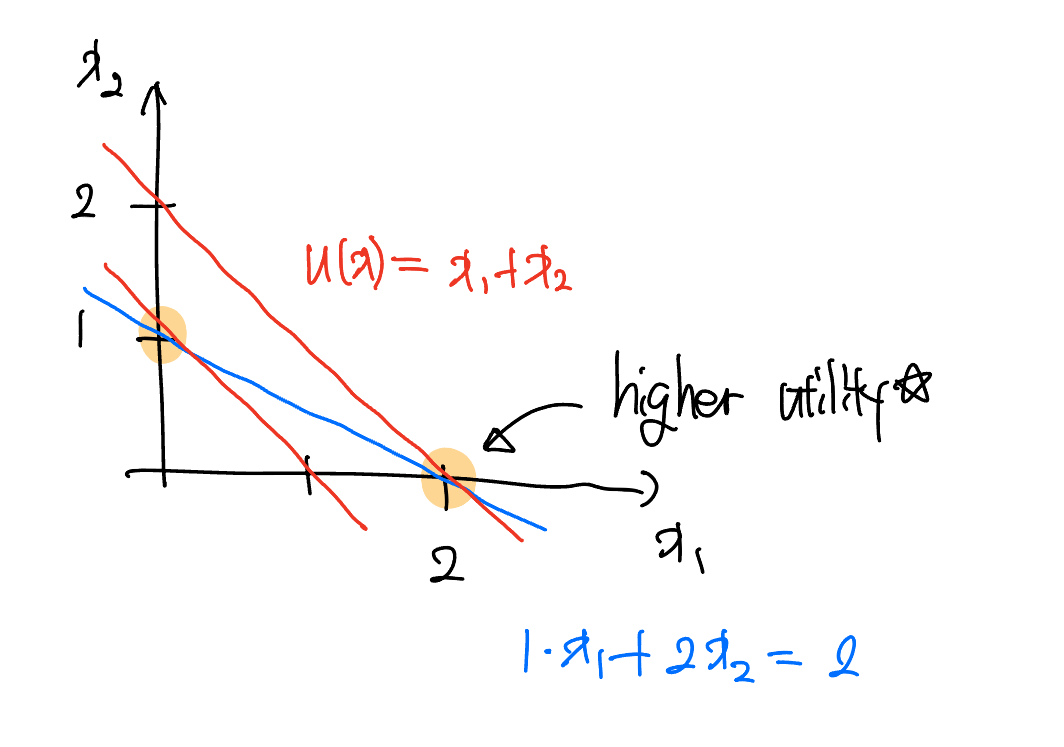
그러면, 소비자는 예산이 얼마있든지 상관없이 모든 예산을 $x_1$에 쏟아부어 $u(x)$를 극대화 하려고 합니다. 따라서, 최적해는 $(x^{\ast}_1, 0)$으로 경계해에서 만들어집니다.

Strong Preference

이번에는 효용 함수가 $u(x) = x_1$으로 오직 재화1에 대해서만 효용을 줍니다. 재화2는 전혀 관심이 없습니다.

이 경우 가격비와 상관 없이, 소비자는 모든 예산을 재화 1에 최대한 많이 소비합니다. 따라서, 최적해는 $(x^{\ast}_1, 0)$으로 경계해에서 만들어집니다.

Undesirable Goods

만약 효용 함수가 $u(x) = x_1 - x_2$라면, 재화2는 가지고 있을수록 손해 입니다.

따라서, 가격비와 상관 없이, 소비자는 모든 예산을 재화 1에 최대한 많이 소비합니다. 따라서, 최적해는 $(x^{\ast}_1, 0)$으로 경계해에서 만들어집니다.

Internal Examples

내부해가 생기는 경우는, 보통 효용 함수가 아래와 같은 형태일 때 발생합니다!

\[u(x) = x_1^{\alpha} x_2^{\beta}\]

참고로 이런 형태의 효용 함수를 “Cobb-Douglas(콥-더글라스)” 효용 함수라고 합니다!

Equal Preference

효용 함수가 $u(x) = x_1 x_2$이고, 예산 집합이 $1 \cdot x_1 + 2 \cdot x_2 = 2$로 주어졌습니다.

이때, 문제를 최적화 문제를 풀면 됩니다!

$x_1 = 2 - 2 x_2$로 정리하고, 이것을 효용 함수에 대입하면,

\[u(x) = (2 - 2 x_2) x_2 = 2 x_2 - 2 x_2^2\]

최댓값을 찾기 위해 미분값이 0이 되는 지점을 찾습니다.

\[\frac{u(x)}{dx_2} = 2 - 4 x_2 = 0\]

그러면, $x_2 = 1/2$가 됩니다. 그리고, $x_1 = 1$이 됩니다. 따라서, 최적해는

\[x^{\ast} = (1, 1/2)\]

이 최적해는 (정의에 따라) “내부해”입니다!

Perfect Complementary

이번에는 효용 함수가 미분 불가능 하지만, 내부해를 찾을 수 있는 경우 입니다.

완전 보완재는 효용 함수가 $u(x) = \min(x_1, x_2)$입니다. 이 경우, 최적해는 꼭짓점에서 이루어집니다.

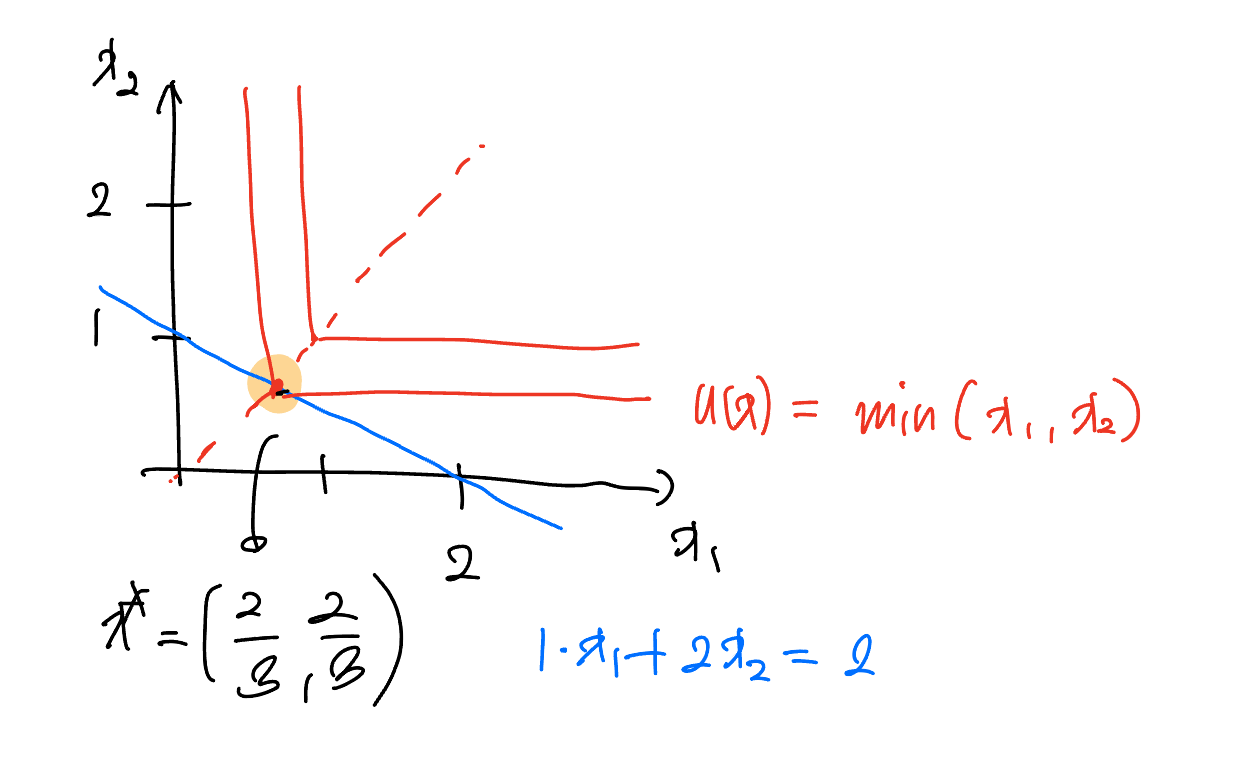
그리고 이 점은 “내부해”입니다!

맺음말

다음 포스트에선 수요 함수 $x(B)$의 합리성(Rationality)에 대해서 다룹니다!

➡️ Rational Demand Functions