Euler Method

수학과 복수전공을 위해 졸업 마지막 학기에 “수치해석개론” 수업을 듣게 되었습니다. 수학과 졸업시험도 겸사겸사 준비할 겸 화이팅 해봅시다!! 전체 포스트는 “Numerical Analysis“에서 확인할 수 있습니다.

들어가며

많은 자연현상이 미분방정식의 형태로 모델링 되지만, 대부분의 미분방정식은 “해석적인 해(analytic solution)”을 구하지 쉽지 않습니다. 이럴 때에 수치해석적인 접근으로 근사해를 찾아서 많은 문제들을 해결할 수 있다고 합니다.

예를 들어, 아래와 같은 미방은 우리가 쉽게 해석적 해를 구할 수 있습니다.

\[y' = 2t \rightarrow y(t) = t^2 + C\]

그런데, 복잡한 미방이라면, 해석적 해를 쉽게 구할 수 없습니다. 예를 들어, 아래와 같은 미방은 쉽게 구할 수 없습니다.

\[y' = y^2 - \sin (t) + e^{-y}\]

이런 미방들에 대해 수치적인 근사값을 구하기 위해서 수치해석 수업에서 미분방정식의 문제들을 다루게 됩니다!

First Step to Numerical Methods for ODEs

아래와 같은 미분방정식이 있다고 합시다.

\[u'(t) = - u(t)\]

그리고 초기값은 $u(0) = 1$ 입니다. 이것을 해석적인 방법을 이용해 충실히 풀어내면, $u(t) = e^{-t}$라는 해를 얻게 됩니다. 이걸 수치적인 방법으로도 풀어봅시다!

미분 $u’(t)$를 아래와 같이 평균 변화율로 근사합니다.

\[u'(t) \approx \frac{u_{n+1} - u_n}{h}\]

그리고 이를 처음의 ODE에 적용해보면

\[\frac{u_{n+1} - u_n}{h} = - u_n(t)\]

식을 정리해보면

\[u_{n+1} = u_n - h u_n\]

이제 초기값 $u(0) = 1$을 사용해 값을 재귀적으로 구해봅시다. $h = 0.1$로 둡니다.

\[u_1 = u_0 - h \cdot u_0 = 1 - 0.1 \cdot 1 = 0.9\]

이어서 계속하면

\[\begin{aligned} u_2 &= 0.9 - 0.1 \cdot 0.9 = 0.81 \\ u_3 &= 0.81 - 0.1 \cdot 0.81 = 0.729 \\ u_4 &= 0.729 - 0.1 \cdot 0.729 = 0.6561 \end{aligned}\]

이것을 해석적으로 얻은 $e^{-t}$의 값과 비교해보면 값에 조금 차이는 있지만, 경향은 거의 따라간다는 것을 확인할 수 있습니다. 이 방법을 “Euler’s Method”라고 합니다!

Euler’s Method

오일러 방법은 현재 위치 $t$와 그곳에서의 기울기 $u’$를 안다면, 그 방향으로 다음 위치를 예측하여 함수값을 찾아내는 수치적 방법 입니다.

$u(t+h)$의 값을 알기 위해 테일러 전개를 해봅시다. 그러면,

\[u(t+h) = u(t) + h u'(t) + \frac{h^2}{2} u''(t) + \cdots\]

이때, 오일러 방법은 첫번째 항까지만 사용합니다.

\[u(t+h) \approx u(t) + h u'(t)\]

우리는 ODE를 다음과 같이 알고 있습니다.

\[u'(t) = f(t, u)\]

이걸 테일러 근사한 식에 대입하면,

\[u(t+h) \approx u(t) + h {\color{red} f(t, u(t))}\]

이걸 반복해서 수행한다면,

\[u(t + (n+1)h) \approx u(t + nh) + h f(t + nh, u(t+nh))\]

이것을 기호를 통해 간단하게 바꾼 것이 아래의 점화식 입니다.

\[u_{n+1} \approx u_n + h f(t_n, u_n)\]

이 방식은 솔루션 함수 $u(t)$의 함숫값을 구하기 때문에, “explicit method”라고 부릅니다. 그리고 시간이 나아감에 따른 솔루션의 함수값 변화를 계산하기 때문에 “time-marching method”라고도 부릅니다.

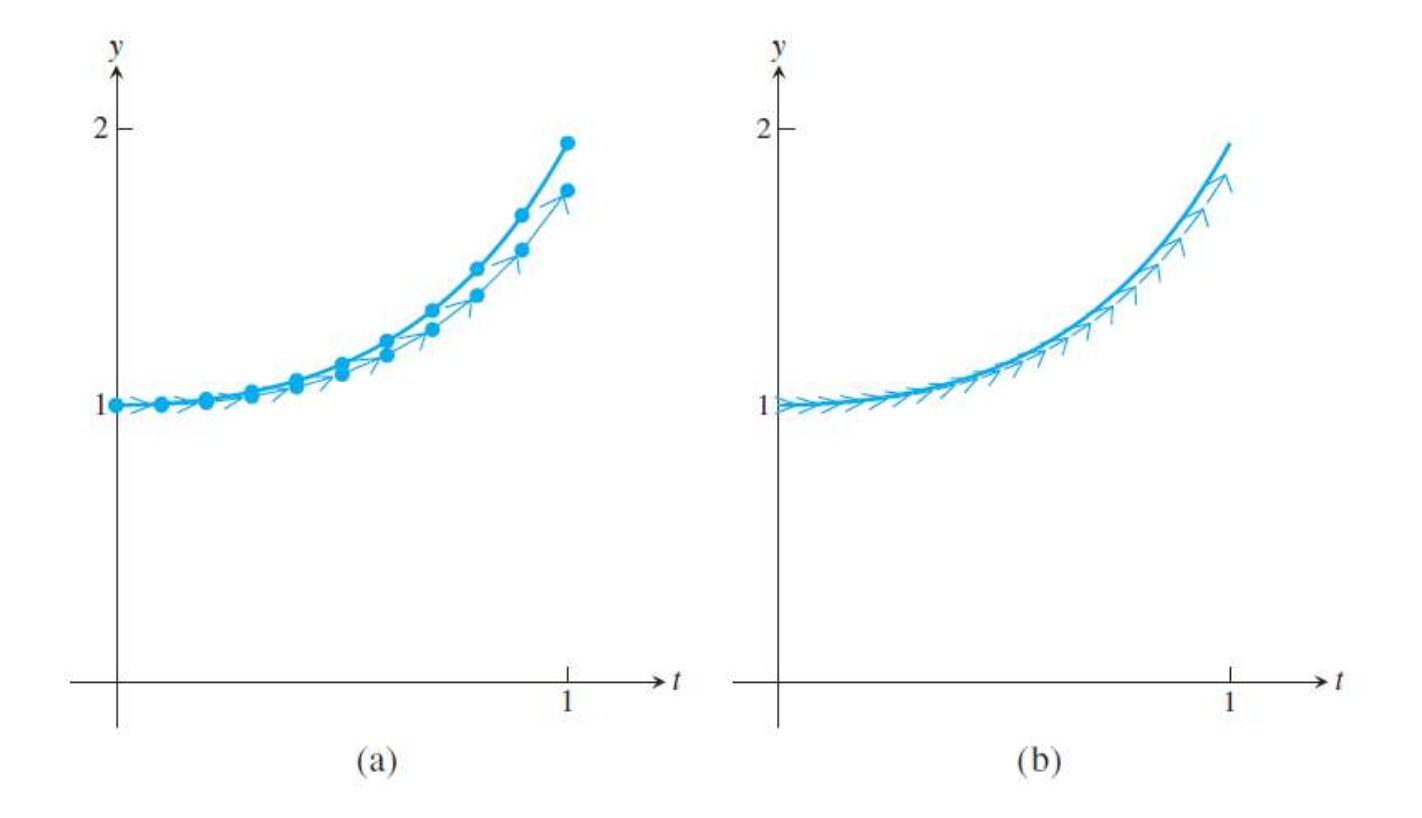
그림은 오일러 방식으로 ODE의 솔루션 함수의 함수값을 구한 결과를 보여줍니다. 좌측은 구간을 10 단계로 나눈 결과, 우측은 구간을 20 단계로 나눈 결과 입니다. 사진으로 볼 수 있듯이 구간을 촘촘하게 나눌 수록 해석적 해로 구하는 함수와의 오차가 줄어듭니다!

Error Analysis

오일러 방식에는 2가지 형태의 오차를 생각할 수 있습니다.

먼저, “전역(Global) 오차” 입니다.

\[e_n = u(t_n) - u_n\]

이것은 여러 스텝을 진행한 후에 누적된 총 오차를 의미 합니다. 솔루션의 함수값과 근사해 사이의 차이 값을 표현 합니다.

오일러 방식에서는 “Local Truncation Error“라는 국소 오차를 정의 합니다. 이것은 변화율의 근사와 실제 기울이의 차이를 계산하여 얻습니다.

$u’(t) = f(t, u)$는 ODE에 의한 실제 기울기 값 입니다. $t_n$에서의 실제 기울기는 $f(t_n, u(t_n))$가 됩니다.

오일러 방법은 기울기를 근사 합니다. 이것은 아래와 같이 구합니다.

\[\frac{u(t_{n+1}) - u(t_n)}{k}\]

이때, 해석적 솔루션인 $u(t)$를 사용하는 것에 유의 합니다.

이 둘의 차이를 구하면, 오일러 방법이 실제 변화율을 얼마나 잘 근사하는지를 측정할 수 있습니다. 따라서, 국소 오차는 아래와 같이 정의 합니다.

\[\tau_n = \left(\frac{u(t_{n+1}) - u(t_n)}{k}\right) - f(t_n, u(t_n))\]

실제 해는 곡선처럼 구부러져 있습니다. 하지만, 오일러 방법은 “직선”으로 근사합니다. 그래서 곡선을 일직선으로 근사함으로써 생기는 오차가 “Local Truncation Error”가 됩니다.

Degree of Error

오차의 차수를 계산해봅시다. 이를 위해 $u(t_{n+1})$에 대해 테일러 전개를 수행합니다.

\[\begin{aligned} u(t_{n+1}) &= u(t_n + k) \\ &= u(t_n) + k u'(t_n) + \frac{k^2}{2!} u''(\xi_n) \end{aligned}\]

이것을 국소 오차 $\tau_n$에 대입해보면

\[\begin{aligned} \tau_n &= \left(\frac{u(t_{n+1}) - u(t_n)}{k}\right) - f(t_n, u(t_n)) \\ &= \frac{\left(\cancel{u(t_n)} + k u'(t_n) + \frac{k^2}{2} u(\xi_n)\right) \cancel{- u(t_n)}}{k} - u'(t_n) \\ &= \left(u'(t_n) - \frac{k}{2} u''(\xi_n) \right) - u'(t_n) \\ &= \frac{k}{2} u''(\xi_n) \end{aligned}\]

따라서, 최종적으로 남은 것은

\[\tau_n = \frac{u''(\xi_n)}{2} k = O(k)\]

즉, 시간 간격 $k$에 비례하므로 오차의 정확도는 “1차 정확도”를 갖습니다.

Example

$u’’ > 0$, $t > 0$일 때, 근사값 $u_{n}$은 왜 실제값 $u(t_n)$보다 under-estimate 되는지 설명하라. (23년도 졸업시험 기출)

$u(t_{n+1} = t_n + k)$에 대해 테일러 전개하면,

\[u(t_{n+1}) = u(t_n) + k u'(t_n) + \frac{k^2}{2} u''(\xi_n)\]

이때, 오일러 방식은 뒤의 $\frac{k^2}{2} u’’(\xi_n)$ 텀은 사용하지 않습니다. 따라서, 그 부분만큼 오차가 발생합니다. 이때, $u’’ > 0$라면, 실제값 $u(t_n)$과 비교해 $u_n$의 값은 더 작아지게 됩니다.

이런 오차는 iteration이 진행되면서 누적되고, 아주 긴 시간이 지나 $t \rightarrow 0$가 되면, 결국 실제값과 근사값의 차이가 커지게 됩니다.

\[\lim_{n \rightarrow \infty} (u(t_n) - u_n ) = + \infty\]

Degree of Error (Global)

TODO…

Limitation

오일러 방식이 꽤 괜찮아 보이지만, 어떤 ODE에서는 수치적 방법의 성능이 급격히 떨어집니다.

예를 들어 아래와 같은 ODE를 수치적 방법으로 풀어본다고 해봅시다.

\[u' = - 4 t^3 y^2, \quad -10 \le t \le 0, \quad u(-10) = \frac{1}{10001}\]

이때, 해석적 해는 $u(t) = 1 / (t^4 + 1)$로 구할 수 있습니다. 그리고 $u(0) = 1$이 됩니다.

표면적으로는 이 ODE는 나이스 합니다. 해는 부드럽고, 해석적 해도 존재하고 구할 수 있습니다! 그런데, 오일러 방식은 이 문제를 풀 때 매우 부정확한 근사를 제공 합니다.

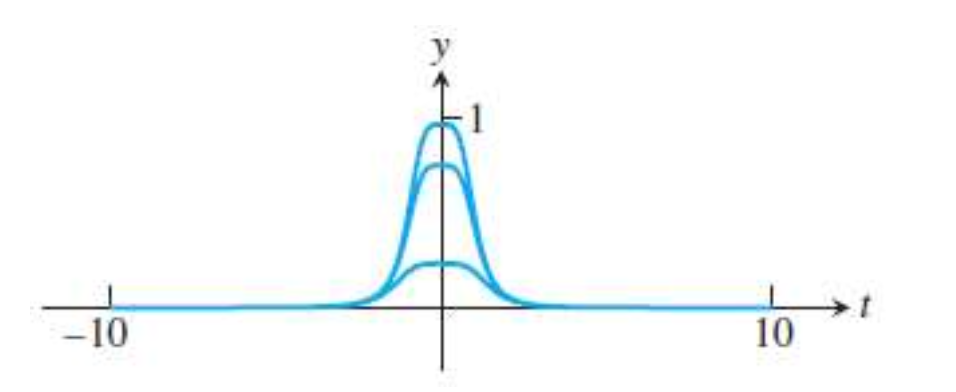
실제로 $h = 10^{-3}, 10^{-4}, 10^{-5}$ 스텝 사이즈로 근사를 하게 되면, 스텝을 아주 작은 $10^{-5}$ 정도는 해야 겨우 $u(0) = 1$에 가까워집니다. 그러나 이것은 정확한 근사에 도달하기 위해서는 아주 작은 스텝이 필요하다는 것이며, 그 과정에서 수많은 계산 과정이 필요하다는 것을 말합니다.

Floating Point Error

그리고 다른 수치적 근사도 모두 겪는 Floating Point에 의한 오차를 컴퓨터로 계산할 때, 겪습니다.

일단 내용을 한번 훑고 싶어서 이 부분은 스킵 하겠습니다!

맺음말

미분방정식으로 수치적으로 접근하는 첫 걸음을 내딛었습니다! 🧑‍🚀

하지만 “오일러 방법”에도 한계가 분명히 있었습니다! 다음 포스트에선 오일러 방법을 개선한 버전을 살펴보도록 하겠습니다.