Competitive Equilibrium of Indivisible Exchange Economy

졸업을 위해 마지막 학기에 “미시경제학” 수업을 듣게 되었습니다. 경제학원론 수업을 재밌게 들어서 경제 쪽이랑 궁합이 좋은 줄 알고 신청 했는데, 웬걸… 이 과목은 사실상 수학과 과목 이었습니다.. ㅋㅋ 그래도 수학과 복수전공도 하고 있으니, 이 수업도 힘내서 잘 들어봅시다! 전체 포스트는 “미시경제학” 카테고리에서 확인하실 수 있습니다.

들어가며

지난 포스트에서 이산 교환 경제에 대해 모델링 하고, 어떻게 동작하는지 사례를 살펴보았습니다.

이번 포스트부터는 이산 교환 경쟁에서 어떻게 균형이 형성 되는지를 살펴봅니다.

Competitive Equilibrium of Indivisible Exchange Economy

이산 교환 경제에서 “경쟁 균형(Competitive Equilibrium)“은 아래와 같은 조건을 만족하는 균형 상태 입니다.

• Optimality of Choices
  • 각 개인 $i$는 아래 조건에 따라 최적의 선택을 합니다.
  • 만약 $p < v_i$라면
    • $a_2(i) = 1$, 개인은 반드시 구매를 합니다.
  • 만약 $p > v_i$라면
    • $a_2(i) = 0$, 개인은 절대 구매하지 않습니다.
  • $a_1(i) = e_1(i) + p\cdot (e_2(i) - a_2(i))$
    • 개인의 최종 재화는 위의 공식을 따릅니다.
• Feasibility
  • $\sum a(i) = \sum e(i)$
  • 연속 교환 경제에서도 성립했던 등식 입니다!

Walras’s Law

연속 교환 경제에서 봤던 정리가 이산 교환 경제에서도 성립 합니다.

이산 재화에 대한 수요의 총합이 공급의 총합과 같다면,
연속 재화(Money)에 대한 수요 총합과 공급 총합도 같다진다.

즉, 재화 시장이 Feasibility를 만족한다면, 돈의 흐름도 저절로 Feasibility를 이루게 됩니다.

Example

앞에서 봤던 예제를 다시 봅시다.

구매자 $B_4$, $B_{10}$ 그리고 판매자 $S_0$, $S_6$가 있을 때…

경쟁 균형이 성립하기 위해서는 가격이 $4 \le p \le 6$이 되어야 합니다. 이 가격에서는 모든 구매자가 구매할 의향이 있고, 모든 판매자가 물건을 판매할 의향이 있습니다.

자세히 살펴보면,

• $p = 4$
  • $B_{10}$은 구매 의향이 있고, 구매를 해야 합니다.
  • $S_0$는 판매 의향이 있고, 판매를 해야 합니다.
  • 반면에, $B_4$는 구매를 해도 되고, 안 해도 됩니다. (무차별)
  • 반면에, $S_6$는 판매 의향이 없습니다.
  • 따라서, 거래는 $(B_{10}, S_0)$ 사이에 한 건만 거래 됩니다.
• $p = 5$
  • $B_{10}$은 구매 의향이 있고, 구매를 해야 합니다.
  • $S_0$는 판매 의향이 있고, 판매를 해야 합니다.
  • 반면에, $B_4$는 가격이 바싸서 구매할 의향이 없습니다.
  • 반면에, $S_6$는 판매 의향이 없습니다.
  • 따라서, 거래는 $(B_{10}, S_0)$ 사이에 한 건만 거래 됩니다.
• $p = 6$
  • $B_{10}$은 구매 의향이 있고, 구매를 해야 합니다.
  • $S_0$는 판매 의향이 있고, 판매를 해야 합니다.
  • 반면에, $B_4$는 가격이 바싸서 구매할 의향이 없습니다.
  • 반면에, $S_6$는 판매를 해도 되고, 안 해도 됩니다. (무차별)
  • 따라서, 거래는 $(B_{10}, S_0)$ 사이에 한 건만 거래 됩니다.

그런데, $p = 7$이 되어버린다면,

• $p=7$
  • $B_{10}$은 구매 의향이 있고, 구매를 해야 합니다.
  • $S_0$는 판매 의향이 있고, 판매를 해야 합니다.
  • 반면에, $B_4$는 가격이 바싸서 구매할 의향이 없습니다.
  • 반면에, $S_6$는 판매 의향이 있고, 판매를 해야 합니다.
  • 거래는 $(B_{10}, S_0)$ 또는 거래는 $(B_{10}, S_6)$ 사이에 한 건 거래 됩니다. 하지만, 판매를 못한 판매자 한명이 남게 되기 때문에, 균형이 이뤄지지 않습니다.

Example - 2

이번에는 $S_0$인 판매자가 14명 있고, $B_{100}$인 구매자가 17명 있습니다.

이런 상황에서 경쟁 균형의 가격은 어떻게 될까요?

• $p < 100$
  • 구매자 17명이 모두 재화를 사고 싶어합니다.
  • 판매자 14명도 모두 재화를 팔고 싶어합니다.
  • 그러나 “수요 > 공급”인 “초과 수요”이기 때문에 균형이 이뤄지지 않습니다.
• $p > 100$
  • 구매자 17명 모두 재화를 구매하지 않습니다.
  • 판매자 14명은 모두 재화를 팔고 싶어합니다.
  • “수요 < 공급”인 “초과 공급”입니다. 따라서 균형이 이뤄지지 않습니다.
• $p = 100$
  • 구매자 17명 모두 무차별한 가격 입니다.
  • 판매자 14명은 모두 재화를 팔고 싶어합니다.
  • 구매자 중 14명이 판매자 14명과 선택적으로 거래를 합니다. 나머지 3명의 구매자는 안 사도 됩니다.
  • 이때는 “수요 = 공급”이 되고, 경쟁 균형이 성립합니다!

이것은 “경쟁 균형”이 이뤄지기 위해서 꼭 거래가 이뤄져야 하는게 아님을 알려줍니다. 어떤 아주 특수한 상황에서는 아무도 사고팔지 않는데도 균형이 이뤄질 수 있습니다. 예를 들어, 구매자/판매자 모두 $B_{100}$, $S_{100}$이라면, $p=100$인 가격에서 아무도 거래를 하지 않아도 균형이 성립 합니다.

Characterization of Competitive Equilibrium

이산 교환 경제 $<N, (v_i)_{i\in N}, e>$가 주어졌습니다. 이때, 개인의 Personal Valuation을 가치가 높은 것에서 낮은 것으로, 내림차순으로 정렬 합니다. 가치 정렬은 판매자인지 구매자인지 구분하지 않고 진행합니다.

\[v_1 \ge v_2 \ge \cdots \ge v_n\]

그리고 $s$를 재화를 보유하고 판매 가능한 사람의 수라고 합니다. 이것은 현재 시장에 있는 “매물의 총량”이라고 합니다.

그러면, 균형 가격은 아래 범위에서 형성 됩니다.

\[v_{s+1} \le p \le v_s\]

즉, 재화를 받는 상위 $s$명과 재화를 받지 못하는 아래 $N - s$명 사이에서 형성 됩니다.

• $p \le v_s$
  • 를 만족하는 상위 $s$명은 구매할 의향이 있고, 실제로 구매 합니다.
• $v_{s+1} \le p$
  • 를 만족하는 하위 $N - s$명은 사고 싶지 않거나 무차별 합니다.

Proof

위의 명제가 참인지 살펴보려면, 경쟁 균형을 만족하기 위해 2가지 조건을 체크하면 됩니다.

1. Optimality Condition

• $p \le v_i$
  • 인 상위 $s$명은 구매를 해도 되는 합리적인 선택을 합니다.
• $v_i \le p$
  • 인 하위 $n-s$명은 구매 하지 않아도 되는 합리적인 선택을 합니다.

즉, 모든 개인은 자기에게 최적인 선택을 합니다.

---

2. Feasibility

이런 상태에서 교환이 일어나도

• 총 재화 수요는 $\sum a_2(i) = s$이고,
• 총 재화 공급도 $\sum e_2(i) = s$로

재화의 수요와 공급이 일치 합니다.

Graphical View

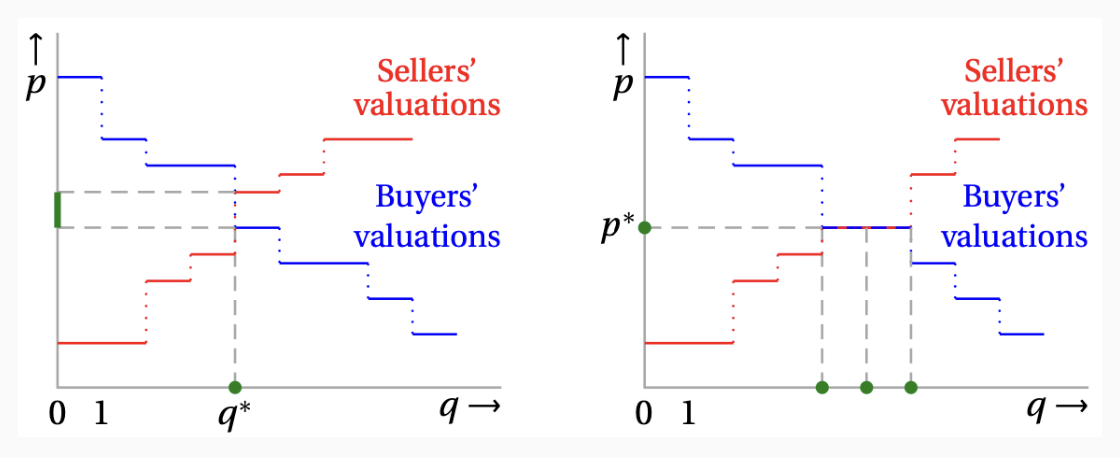
경쟁균형의 가격과 거래량이 어떻게 이뤄지는지 시각적으로 보여주는 그림 입니다. 왼쪽과 오른쪽의 상황이 다릅니다.

각각은 판매자의 가치 평가와 구매자의 가치 평가가 표시 되어 있습니다. 판매자는 가격이 커질수록 거래량이 늘어납니다. 반면에, 구매자는 가격이 높아질수록 거래량이 줄어듭니다.

[왼쪽]

두 계단 그래프가 교차하는 시점에서

\[\text{# of Seller} \ge \text{# of Buyer}\]

가 됩니다. 이때, 가장 낮은 구매자의 가치는 $v_s$ 입니다.

균형 거래량은 $q^{\ast} = s$로 표현되고, 균형 가격은 $v_{s+1} \le p \le v_s$의 구간으로 표현됩니다.

[오른쪽]

이 경우는 균형 가격이 정확히 $p^{\ast}$로 고정 됩니다.

이 가격에서 구매자들 중 일부는 $v_i = p$로 무차별적 선호를 보입니다. 이것은 판매자들 중 일부도 마찬가지 입니다.

수평으로 겹치는 계단이 이것을 의미하며, 이것은 무차별적인 다수의 거래량이 균형이 될 수 있음을 말합니다.

왼쪽과 오른쪽 모두 하나의 균형이 아니라 구간이나, 범위의 형태로 균형이 나왔습니다. 그런데 한 하나의 균형이 존재하도록 할 수도 있는데요!

\[v_s = v_{s+1}\]

인 상황이라면, 경쟁 균형이 유일하게 존재합니다!

Example

TDB

Pareto Stable Allocation

이산 교환 경제 $<N, (v_i)_{i\in N}, e>$에서 할당 $a$가 파레토 안정이 되려면,

교환이 이뤄지고 난 후, 재화를 가진 $i$와 재화를 가지지 못한 $j$에 대한 임의의 쌍 $(i, j)$에 대해 재화를 가진 사람은 가지지 못한 사람보다 그 가치를 더 높게 평가해야 한다.

\[v_i \ge v_j\]

아니면, 재화를 가지지 못한 사람의 가진 돈보다 $i$가 매긴 가치가 더 커야 합니다.

\[v_i \ge a_1(j)\]

둘을 종합하면,

\[v_i \ge \min(v_j, a_1(j))\]

그리고, 경쟁 균형 할당은 항상 파레토 안정적 입니다.

저는 $v_i \ge a_1(j)$ 부분이 잘 이해가 안 되었는데요 🤔 요게 $a_(j)$를 거래가 이뤄진 가격으로 이해하면 되더라구요!

일단 거래는 $v_i \ge p$인 가격에서 이뤄집니다. 그런데, 거래가 이뤄지면 그 가격만큼 기존에 재화를 가졌던 사람의 화폐 재화가 추가 됩니다. 따라서,

\[v_i \ge \left(p = a_1(j)\right) \ge v_j\]

라고 보면 될 것 같습니다!

Core and Competitive Equilibrium

Every allocation $a$ in the core of a indivisible exchange economy, there is a number $p$ s.t. $(p, a)$ which is a competitive equilibrium of the economy.