Production Economy

졸업을 위해 마지막 학기에 “미시경제학” 수업을 듣게 되었습니다. 경제학원론 수업을 재밌게 들어서 경제 쪽이랑 궁합이 좋은 줄 알고 신청 했는데, 웬걸… 이 과목은 사실상 수학과 과목 이었습니다.. ㅋㅋ 그래도 수학과 복수전공도 하고 있으니, 이 수업도 힘내서 잘 들어봅시다! 전체 포스트는 “미시경제학” 카테고리에서 확인하실 수 있습니다.

들어가며

새로운 챕터의 시작 입니다!

Introduction

하루가 오전(morning)과 오후(afternoon), 두 시점으로 나뉜다고 가정 합니다. 오전에는 어떻게 생산할 것인지를 결정하고, 오후에는 어떻게 소비할 것인지를 결정 합니다.

“하루 동안” 모든 경제 주체는 “동일한 가격 체계”를 보고 결정 합니다. 하루가 지나면 가격이 바뀔 수는 있지만, 하루 동안은 가격이 고정 되어 있고 이것은 모든 사람에게 동일하게 적용 됩니다.

얼만큼을 생산할 것인지는 공장의 관리자(Manager)가 운영하지만, 그것에 대한 소유권은 소비자들에게 있습니다. …?

오전에 생산 관리자는 생산 계획을 세웁니다. 관리자의 목표는 이윤의 극대화 이며, 모든 생산물은 주어진 가격에 판매된다고 가정 합니다.

오후에는 생산-판매로 인한 이윤이 소유자(=소비자)들에게 분배됩니다. 각 개인은 생산으로부터 얼마나 수익을 받았는지 이때 알 수 있습니다.

개인은 자신의 소득(= 이윤 배당)을 바탕으로 소비 계획을 세웁니다. 이때의 선택은 예사 제약과 주어진 가격 하에 최적 소비 선택을 따릅니다.

Market Equilibrium

시장에 초과 생산과 초과 수요가 없는, 생산과 수요가 일치하고, 모든 잉여 재화가 없어서 소비자 만족이 극대화된 상태라면, 이것을 “시장 균형” 상태라고 합니다.

만약, 초과 공급이 있거나 초과 수요가 있다면 “시장 불균형” 상태라고 합니다. 이때 시장은 가격을 조정하여 균형을 맞추려고 합니다.

Model

아래와 같이 경제를 모델링 합니다.

• 오직 “2개의 재화”만 있다고 가정 합니다.
• $I$는 소비자 집합, $J$는 생산자 집합을 이룹니다.
• 각 소비자 $i$는
  • Increasing, Continuous, Convex
  • 성질이 있는 선호를 가집니다.
• 각 생산자 $j$는
  • 생산 가능한 재화 조합에 대한 집합인 $T(j)$를 가집니다.
  • 이 집합을 “기술 집합(Technology Set)“이라고 부르고,
  • 생산자가 현실적으로 맨들어낼 수 있는 모든 재화 조합을 나타냅니다.

Technology Set

“기술 집합”은 생산자가 선택할 수 있는 생산 가능한 번들의 집합 입니다.

기술 집합은 항상 원점 $O = (0, 0)$를 포함합니다. 즉, 아무것도 생산하지 않는 경우를 포함합니다.

그리고 기술 집합에 속한 어떤 한 점 $(z_1, z_2) \in T$에 대해서 아래가 성립 합니다.

For all $(y_1, y_2)$ s.t.

\[y_1 \le z_1 \quad \text{and} \quad y_2 \le z_2\]

also belongs to technology set $T$.

Free Disposal

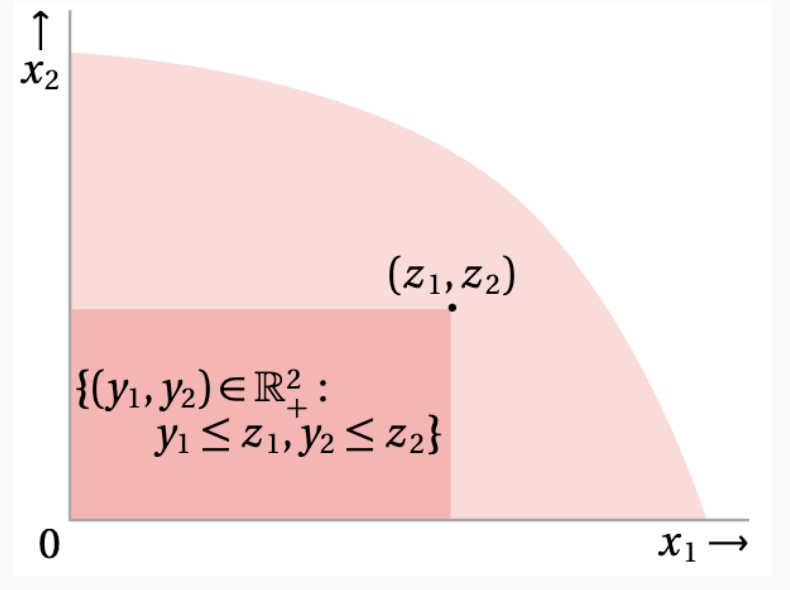
아까 살펴본

\[y_1 \le z_1 \quad \text{and} \quad y_2 \le z_2\]

성질을 “자유 폐기성(free disposal)“이라고 합니다.

이것은 생산 가능한 $(z_1, z_2) 것보다 더 적게 생산하는 조합도 항상 기술 집합에 포함됨을 말합니다.

이것은 생산자가 잉여 생산분을 저장하지 않고, 모두 즉시 폐기한다는 것을 말합니다. 만약 잉여 생산분을 저장해야 한다면 저장 비용을 고려해야 하기 때문에 시장을 분석하는게 복잡해집니다.

Production Economy

생산자 $j$는 시장에 주어진 가격 체계 $p = (p_1, p_2)$ 위에서 자신의 기술 집합 $T(j)$ 내의 생산 가능한 조합 중 하나를 선택해 매출을 최대화 하는 것을 목표로 합니다. 즉,

\[\underset{x \in T(j)}{\text{argmax}} \;\; p \cdot x\]

소비자의 소득은 어디에서 오는가?

생산자가 물건을 팔아서 생긴 이윤(profit)은 소비자에게 분배 됩니다. 즉, 이윤이 곧 소비자의 소득(wealth)가 되어 소비자의 소비 결정에 바탕이 된다는 것 입니다.

그래서 “생산 → 이윤 → 소득 → 소비”라는 순환 고리가 만들어지게 됩니다.

생산자와 소비자가 동일한 사람인가?

이제 설명을 잘 해야 하는데, 실제로 생산을 하는 “생산자(Producer)”는 실제 사람이 아니라 “법인” 같은 개념으로 봐야 합니다.

법인은 한 사람이 소유할 수도 있고, 여러 명이 소유할 수도 있습니다.

그리고 생산을 하는 인격과 소비를 하는 인격이 분리 되어 있다고 가정 합니다. 법인을 구성하는 소비자는 법인의 이윤을 법인 소유자(=소비자)가 나눠가집니다.

그리고 법인에 대한 소유 비율은 각자 다를 수 있는데, 만약 3명의 소비자가 4:4:2 비율로 나누어 소유 하고 있다면, 그 공장에서 발생하는 이윤도 4:4:2 비율로 소유자(=소비자)에게 분배 됩니다.

Modeling

생산 경제는 5가지 요소로 표현 할 수 있습니다.

\[<I, J, (\succcurlyeq^i)_{i\in I}, T(j), \alpha(i, j)>\]

• Consumers $I$
  • 소비자들의 유한 집합
• Producers $J$
  • 생산자들의 유한 집합
• Preference $(\succcurlyeq^i)_{i\in I}$
  • 각 소비자 $i$별 선호 관계
  • 모든 선호는 Monotone, Continuous, Convex 성질을 만족.
• Technologies $T(j) \subseteq \mathbb{R}^2_{+}$
  • 각 생산자 $j$별로 생산할 수 있는 있는 재화 조합
  • 닫혀 있고, 볼록 하고, 자유 폐기성(free disposal) 성질을 만족.
• Ownership Shares $\alpha(i, j)$
  • 소비자 $i$가 생산자 $j$의 이윤에 대한 소유 비율
  • 단, 비율의 합은 반드시 1이 되어야 함.

Feasible

아래 수식을 만족하는 상태를 말합니다.

\[\sum_{i \in I} x(i) = \sum_{j \in J} y(j)\]

각 재화별로 총 소비량과 총 생산량이 일치 하는 상태를 말합니다. 이 상태를 “Market Clearing” 상태라고도 합니다.

이 조건은 생산 경제에서 균형을 이루는 기본 조건 중 하나 입니다.

Consumption-Production Plan

생산 경제(Production Economy)가 경제의 각 객체와 구조를 정의한 것이라면,

“소비-생산 계획”은 그 구조 안에서 실행 가능한 소비와 생산을 결정한 것 입니다. 이것은 생산 경제의 실행 결과(outcome) 또는 솔루션(allocation)에 대응되는 개념 입니다.

엄밀히 정의하면, 주어진 생산 경제 $<I, J, (\succcurlyeq^i), (T(j)), \alpha>$에 대해 아래 조건을 만족하는 $(x, y) $쌍들의 집합 입니다.

\[\left\{ (x, y) \; : \; x = x(i), y = y(j) \text{ where } y(j) \in T(j) \text{ and } \sum_i x(i) = \sum_j y(j) \right\}\]

단, 이 솔루션이 최적의 솔루션은 아닐 수 있습니다. 누군가는 불만이 있을 수도 있고, 아님 모두의 효용을 증가하는 더 좋은 쌍이 존재할 수 있습니다.

그런 솔루션 중에서 나이스한 솔루션이 “경쟁 균형” 상태 입니다.

Competitive Equilibrium of Production Economy

생산 경제에서 경쟁 균형이 성립하기 위해서는 그 솔루션이 아래의 조건을 만족해야 합니다.

• 가격 체계 $p^{\ast} = (p_1, p_2)$
  • 가 있어야 합니다.
  • 이 가격 체계는 시장에서 거래되는 모든 재화에 대한 가격을 의미 합니다.
• 소비자들의 소비 결정 $x^{\ast}(i)$
  • 는 소비자가 가격 $p^{\ast}$와 자신의 소득(=자신이 소유한 생산자의 이윤 몫)을 바탕으로 자신의 선호에 따라 가장 만족스러운 번들 $x^{\ast}(i)$를 선택합니다.
• 생산자들의 소비 결정 $y^{\ast}(j)$
  • 는 시장 가격 $p^{\ast}$를 고려해, 자신의 기술 $T(j)$ 범위 내에서 이윤을 최대화 하는 생산 번들 $y^{\ast}(j)$를 선택 합니다.
• 총량 조건
  • 생산자들이 생산한 재화 총량은 소비자들이 소비한 재화 총량이 같습니다.
  • $\sum_i x^{\ast}(i) = \sum_j y^{\ast}(j)$

[Optimality of Consumer’s Choice]

\[\left\{ x \in \mathbb{R}^2_{+} \, : \, p \cdot x = \sum_{j \in J} \alpha(i, j) \pi(j) \right\}\]

이때, 이윤 $\pi(j)$는 생산량에 따라 결정됩니다: $\pi(j) = p y(j)$.

[Optimality of Producer’s Choice]

생산자가 생산 가능한 생산량 $y(j) \in T(j)$ 중에 이윤을 극대화 하는 것을 선택 합니다.

\[\underset{y(j) \in T(j)}{\text{argmax}} \;\; p \cdot y(j)\]

[Feasibility]

(자주 봤죠??) 아래의 식을 만족하는 생산-소비 상황 입니다.

\[\sum_i x^{\ast}(i) = \sum_j y^{\ast}(j)\]

Pareto Dominance

주어진 소비-생산 계획 $(x’, y’)$이 다른 계획 $(x, y)$ 보다 더 나이스한 상태라면, 그 계획이 “파레토 지배한다(Pareto dominates)”라고 합니다. 이때, 나이스 여부는

• 모든 소비자에게 손해가 없음
  • $x’(i) \succcurlyeq^i x(i)$
  • 즉, 모든 사람이 파레토 지배 계획을 선호함
• 적어도 한 명에게는 더 나은 선택
  • $x’(i) \succ^i x(i)$
  • 누군가 한 명은 분명 더 행복해집니다.

소비-생산 계획이 “파레토 안정”이라는 것은 이 계획보다 모두에게 손해가 없고, 누군가에게는 너 선호되는 다른 계획이 존재하지 않음을 말합니다. 즉, 계획이 파레토 안정적이라면 개선의 여지 없는 상태라는 것을 말합니다.

Competitive Equilibrium is Pareto Stable

생산 경제에서는 어떤 경쟁 균형이든, 그때의 소비-생산 계획은 항상 파레토 안정적 입니다.

증명은 스킵!

(TODO: 뭔가 중요한 내용이 있어 보여서 나중에 읽어볼 것!)

맺음말

이것으로 생산 경제에 대한 모델링과 그때의 균형 상태에 대해 살펴보았습니다. 다음 포스트도 얼른 살펴봅시다! 화이팅!!

➡️ Economy with Capital and Labor