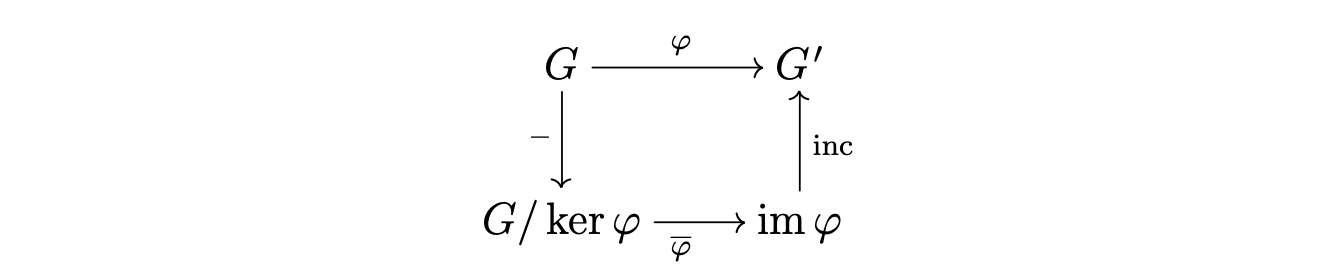Three Isomorphism Theorems
2020-2학기, 대학에서 ‘현대대수1’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :)
지금 다루는 Isomorphism Theorem을 완전히 이해하고 체득한다면, 군론 자체를 아주 깊게 이해할 수 있다 ㅎㅎ
1st Isomorphism Theorem; FHT
첫번재 Isomorphism Theorem은 이전의 포스트에서 이미 다루었다. FHT가 곧 1st Isomorphism Theorem이다!
Theorem. Fundamental Homormophism Theorem (FHT)
Let $\phi: G \longrightarrow G’$ be a group homo-.
Then,
- $\phi[G]$ is a group.
- $G / {\ker \phi} \cong \phi[G]$
Lemma 34.4
Lemma.
Let $N \trianglelefteq G$, $H \le G$.
Then,
- $HN = NH$
- $HN \le G$
만약 $H$ 역시 normal subgroup이라면, $HN \trianglelefteq G$가 된다!
증명이 생각보다 쉽다!
proof.
1. $HN = NH$
Let $h \in H$, $n \in N$.
Then,
\[\begin{aligned} &hnh^{-1} \in N \\ &\implies hn \in Nh \\ &\implies hn = n'h \quad \textrm{for some} \; n' \in N \\ &\implies \therefore HN \subseteq NH \end{aligned}\]반대로 $h^{-1}nh^ \in N$로 잡는다면, $NH \subseteq HN$의 결과를 얻는다.
둘을 종합하면,
\[HN \subseteq NH \; \land \; NH \subseteq HN \implies HN = NH\]$\blacksquare$
2. $HN \le G$
Normal subgp과 일반 subgp만 있다면, $G$에 속하는 새로운 subgp을 유도할 수 있다는 명제다.
간단히 $HN$이 subgp인지 확인하면 된다.
(1) closed under opr
$(HN)(HN) = H(NH)N = H(HN)N = HN$
(2) identity
$e \in H \; \land \; e \in N \implies e \cdot e = e \in HN$
(3) inverse
$(hn)^{-1} = n^{-1} h^{-1} \in NH = HN$
$\blacksquare$
Definition. Subgp generated by set $S$
$< S >$: the subgroup of $G$ generated by $S$
\[< S > \; = \; \underset{S \subseteq H \le G}{\bigcap} H\]이때, intersection of subgps는 여전히 subgp이라는 것이 알려져 있다.
즉, set $S$를 포함하는 subgroup 중 가장 작은 subgroup이 $< S >$이다.
$H$ join $K$
Definition. $H$ join $K$
$H$ join $K$는 subgroup $H$와 $K$를 포함하는 가장 작은 subgroup이다.
※ 이때! 만약 $H \trianglelefteq G$라면, $H \lor K = HK$가 된다!
“만약 $H \trianglelefteq G$라면, $H \lor K = HK$가 된다!”라는 명제에 대해 보충해보고자 한다.
$H \cup K$를 포함하는 subgroup에는 당연히 $H$도 포함하고, $K$도 포함하고, $HK$와 $KH$ 포함하고 있을 것이다.
이때, 운이 좋아 $HK$와 $KH$ 연산으로 이미 Group을 이룬다면, 또 $HK = KH$라면, Lucky! 우리는 $<H \cup K> = HK$로 찾아냈다!!
하지만, 아쉽게도 $HK$가 꼭 Group을 이룬다는 보장은 없다 ㅠㅠ $hk \notin H, K$일 수도 있기 때문이다.
우리가 앞에서 살펴본 Lemma는 $HK$가 Group이 되는 조건을 제시한다.
\[H \trianglelefteq G \; \land \; K \le G \implies HK \le G\]따라서 $H$가 Normal subgp이라면, $H$ join $K$는 $HK$가 된다!!
2nd Isomorphism Theorem
Theorem. 2nd Isomorphism Theorem
Let $H \le G$, $N \trianglelefteq G$.
Then,
\[HN / N \; \cong \; N / {(H \cap N)}\]정리 자체는 정말 간결하다… 하지만, 내용을 한 문장으로 압축해 놓은 것이라 정리를 유도하는 데까지 필요한 뒷배경이 많은 편이다 ㅠㅠ
proof.
먼저 가정인 $H \le G$, $N \trianglelefteq G$로부터 명제의 재료가 되는 factor group $HN/N$을 유도하자. 이 과정에서 앞부분에 나왔던 Lemma를 사용한다.
$H \le G$, $N \trianglelefteq G$이므로 Lemma에 의해 $HN \le G$이다.
Normal subgp에 대해선 아래의 명제가 성립한다.
\[\begin{aligned} &\textrm{For} \quad N \le K \le G, \\ &N \trianglelefteq G \implies N \trianglelefteq K \end{aligned}\]명제의 증명은 간단하니 여기에서는 생-략 한다.
이때, $N \le HN \le G$이고, $N \trianglelefteq G$이므로 $N \trianglelefteq HN$이 된다.
$N$이 $HN$의 normal subgroup이므로
$N$에 대한 $HN$의 Factor Group $HN/N$을 정의할 수 있다!
이번에는 동형식의 우변인 $H / (H \cap N)$을 유도해보자.
만약 $N \trianglelefteq G$라면, $H \cap N \trianglelefteq H$가 성립한다.
따라서 $(H \cap N)$에 대한 $H$의 Factor Group $H / (H \cap N)$을 정의할 수 있다!
드디어 증명의 본게임이다!
아래와 같은 homomorphism $\phi$를 디자인 한다.
\[\begin{aligned} \phi: H &\longrightarrow HN \longrightarrow HN / N \\ h &\longmapsto \; h \quad \longmapsto hN \end{aligned}\]이때, $\phi$는 homo-와 homo-의 합성 이므로 역시 homo-이다.
또한, $\phi(h) = hN$이기 때문에 $\phi$는 onto이다.
이제 이 homo- $\phi$의 kernel을 생각해보자.
우리는 $\ker \phi = H \cap N$이 됨을 보일 것이다.
따라서 $h \in N$이고, $\ker \phi \subseteq H \cap N$이다.
반대로,
\[x \in H \cap N \implies \phi(x) = xN = N\]따라서 $x \in \ker \phi$이고, $\ker \phi \subseteq H \cap N$이다.
따라서 $\ker \phi = H \cap N$이다.
FHT에 의해 $H / {\ker \phi} \cong \phi(H)$이다. 이때, $\phi$가 onto 였으므로 $\phi(H) = HN / N$이다.
따라서
\[H / (H \cap N) \cong HN / N\]3rd Isomorphism Theorem
Theorem. 3rd Isomorphism Theorem
Let $H, K \trianglelefteq G$, $K \le H$
Then,
\[G / H \; \cong \; (G/K) / (H/K)\]$\blacksquare$
유도 과정 자체는 2nd iso- theorem에 비해선 정말 쉬운 편이다 ㅎㅎ
proof.
Define a homomoprhism $\phi$ as
\[\begin{aligned} \phi: G / K &\longrightarrow G / H \\ gK &\longmapsto gH \end{aligned}\]Then, check properties of $\phi$.
(1) well-defined
Supp. $gK = g’K$, then
\[\begin{aligned} &gK = g'K \\ &\implies g(g')^{-1}K = K \\ &\implies g(g')^{-1} \in K \\ &\implies g(g')^{-1} \in H \quad (\because K \le H) \\ &\implies g(g')^{-1} H = H \\ &\implies gH = g'H \end{aligned}\](2) $\phi$ is onto
clear
(3) $\phi$ is a homo-.
$\phi(g_1 K)\phi(g_2 K) = \phi(g_1 g_2 K)$ (by factor representative opr)
따라서 $\phi$는 homomorphism이다.
FHT에 의해
\[(G/K) / \ker \phi \; \cong \; \phi(G/K)\]이때, $\ker \phi$는 아래와 같이 유도할 수 있다.
\[gK \in \ker \phi \implies \phi(gK) = gH = H \implies g \in H\]따라서 $gK = hK \in H/K$이고, $\ker \phi \subseteq H/K$가 된다.
반대로
\[hK \in H/K \implies \phi(hK) = hH = H\]따라서 $hK \in \ker \phi$이고, $H/K \subseteq \ker \phi$이다.
따라서 $\ker \phi = H/K$이다.
다시 FHT에 의해 $(G/K) / \ker \phi \; \cong \; \phi(G/K)$이므로
\[(G/K) / (H/K) \; \cong \; G/H\]$\blacksquare$
드디어 Isomorphism Thm 까지 도달했다!!
앞으로도 군론의 다양한 정리들과 사례들이 기다리고 있으니! 기대하시라!!!