Merge Sort

2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :) 전체 포스트는 Algorithm 포스트에서 확인하실 수 있습니다.

Merge Sort

“정렬“은 알고리즘의 가장 근원이 되는 작업 입니다. 그중에서 “병합 정렬(Merge Sort)”과 “퀵 정렬(Quick Sort)”은 인류 역사에서 최고의 알고리즘이라고 생각 합니다! 👍

Merge Sort는 <분할 정복>을 정말 충실히 수행하는 알고리즘 입니다.

“split the list into two halves, recursively sort each half, and them merge them.”

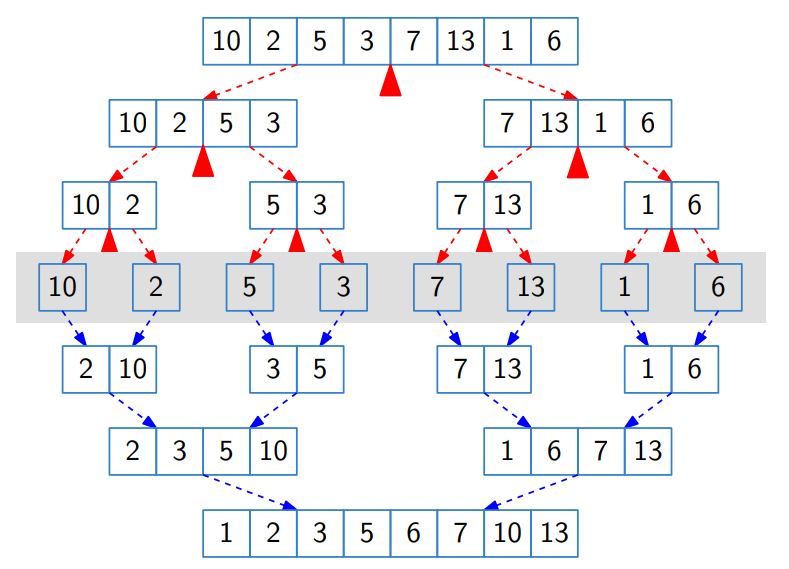
Merge Sort는 기능적으로 봤을 때, “Merge Sort“와 “Merge” 두 가지 작업만 수행하면 된다.

function: mergesort($a[1…n]$)

---

if $n > 1$ then
   return merge(mergesort($a[1 … n/2]$), mergesort($a[n/2+1 … n]$))
else
   return $a$
end if

function: merge($x[1…k]$, $y[1…l]$)

---

if $k=0$:   return $y[1…l]$
if $l=0$:   return $x[1…k]$

if $x[1] \le y[1]$ then
   return $x[1]$ $\circ$ merge($x[2…k]$, $y[1…l]$)
else
   return $y[1]$ $\circ$ merge($x[1…k]$, $y[2…l]$)
end if

이번에는 Complexity를 계산해보자. 점화식을 작성하면 아래와 같다.

\[T(n) = 2 \cdot T(n/2) + O(n)\]

고정 비용 $O(n)$는 merge 작업에서 발생하는 비용이다!

$a=2$, $b=2$, $c=1$이므로, $a/b^c = 2/2 = 1$이다. 따라서 <Master Theorem>에 따라

\[O(n) \cdot \log n = O(n \log n)\]

의 Complexity를 가진다!

Merge Sort는 간단하지만 강력하다! 보통 Merge Sort를 직접 구현하는 경우는 드물지만, 어떤 경우에선 Merge Sort의 아이디어를 채용해서 풀어야 한다!

• Skyline Problem

---

Worst-case Analysis

정렬 알고리즘의 절차는 <트리 Tree>의 형태로 표현할 수 있다. 예를 들어 아래의 트리는 $a_1$, $a_2$, $a_3$ 세 개의 원소에 대한 정렬을 도식화한 그림이다.

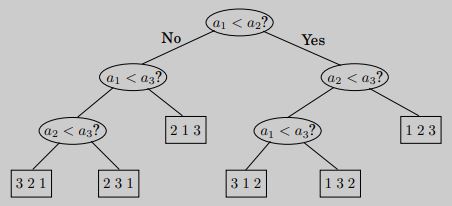
위와 같이 주어진 배열에 대해 원소를 비교하는 모든 경우를 고려하게 되면, 우리는 배열의 $n$개 원소에 대한 가능한 모든 <순열 Permutation>을 확인하는 것과 동일하다. 즉, $n!$ 가짓수의 가능한 순서를 생각한다는 말이다. 이때, “정렬”이라는 작업은 <비교 트리; Comparison Tree>에서 가능한 하나의 <경로 Path>를 취하는 것이라고 할 수 있다.

비교 트리에서 가장 긴 경로(longest path)의 길이를 생각해보자. 비교 트리는 총 $n!$개 만큼의 leaf node를 가지므로 트리의 깊이(depth)는 $\log {(n!)}$이 된다. 이 트리의 “깊이”는 곧 Worst-case에서의 비교 횟수이다!!

약간의 정리들을 활용하면, $\log {(n!)}$에 대해 아래가 성립함을 보일 수 있다.

\[\log {(n!)} \ge c \cdot n \log n \quad \textrm{for some} \; c > 0\]

이것은 함수 $\log {(n!)}$에 대해 $\Omega \left( n \log {n} \right)$임을 의미한다. 그리고 어떤 정렬 알고리즘도 $n$개 원소를 정렬하는 데에 $\Omega (n \log {n})$ 만큼의 비교는 반드시 수행해야 함을 의미한다. 즉, 정렬 알고리즘이 가질 수 있는 Complexity의 하한선이 $n \log {n}$이라는 의미이다.

그런데 우리는 윗 문단에서 <Master Theorem>으로 Merge Sort가 $O(n \log {n})$의 Complexity를 가진다는 걸 유도했다. 즉, Merge Sort의 Complexity가 $n \log {n}$ 보다 절대 높아지지 않는다는 거다! 이 말은 곧 $O(n \log {n})$의 효율을 갖는 Merge Sort가 optimal 정렬 방식이라는 것을 말한다!! $\blacksquare$

p.s. 본인도 처음에는 이해가 잘 되질 않았다. 아마 $\Omega (n \log {n})$의 의미가 잘 와닿지 않았던 것 같은데, 본인은 $\Omega (n \log {n})$를 Complextiy의 하한선이라고 해석했다. 즉, 정렬 알고리즘이 $\Omega (n \log {n})$의 Complexity를 갖는다는 건 모든 정렬 알고리즘은 $n \log {n}$ 보다 크거나 같은 Complexity를 가질 수 밖에 없다고 해석했다는 말이다. 그런데 Merge Sort는 $O(n \log {n})$의 Complextiy를 가지니, 절대 $n \log {n}$ 이상으로는 Complexity가 커지지 않는다. 그러니 $O(n \log {n)}$은 $\Omega(n \log {n)}$ 상황에서 optimal 일 수 밖에 없다!

---

Implementation

아래 코드는 본인 스타일 대로 구현한 Merge Sort 코드다. 원래는 배열을 사용해 공간 사용이 $O(1)$인 “In-place”로 구현해보려고 했는데, 뭔가 코드가 예쁘게 나오지 않을 것 같아서 vector STL과 공간 사용이 $O(N \log N)$인 방식으로 구현해봤다.

vector<int> merge(vector<int> left, vector<int> right) {
  int left_idx = 0, right_idx = 0;

  vector<int> sorted;

  while((left_idx < left.size()) && (right_idx < right.size())) {
    if (left[left_idx] <= right[right_idx]) {
      sorted.push_back(left[left_idx]);
      left_idx += 1;
    } else {
      sorted.push_back(right[right_idx]);
      right_idx += 1;
    }
  }

  for (int i = left_idx; i < left.size(); i++) {
    sorted.push_back(left[i]);
  }

  for (int i = right_idx; i < right.size(); i++) {
    sorted.push_back(right[i]);
  }

  return sorted;

}

vector<int> mergeSort(vector<int> arr) {
  if (arr.size() <= 1) {
    return arr;
  }
  int mid = arr.size() / 2;
  vector<int> leftSide = mergeSort(vector<int>(arr.begin(), arr.begin() + mid));
  vector<int> rightSide = mergeSort(vector<int>(arr.begin() + mid, arr.end()));

  return merge(leftSide, rightSide);
}

개인적인 경험으론 MergeSort는 python으로 구현하는게 가장 쉽고 편하다! 아래는 Leetcode의 Sort an Array 문제를 해결한 코드이다.

class Solution:
    @staticmethod
    def merge(left, right):
        sorted = []
        l_idx = r_idx = 0
        while (l_idx < len(left) and r_idx < len(right)):
            if left[l_idx] <= right[r_idx]:
                sorted.append(left[l_idx])
                l_idx += 1
            else:
                sorted.append(right[r_idx])
                r_idx += 1

        for i in range(l_idx, len(left)):
            sorted.append(left[i])
        for j in range(r_idx, len(right)):
            sorted.append(right[j])
        return sorted

    def sortArray(self, nums: List[int]) -> List[int]:
        if len(nums) <= 1:
            return nums

        mid = len(nums) // 2

        left = self.sortArray(nums[:mid])
        right = self.sortArray(nums[mid:])

        return Solution.merge(left, right)

In-place Implementation

공간 사용이 $O(1)$인 구현입니다. Leetcode의 Sort List 문제를 풀기 위해 구현하였습니다.

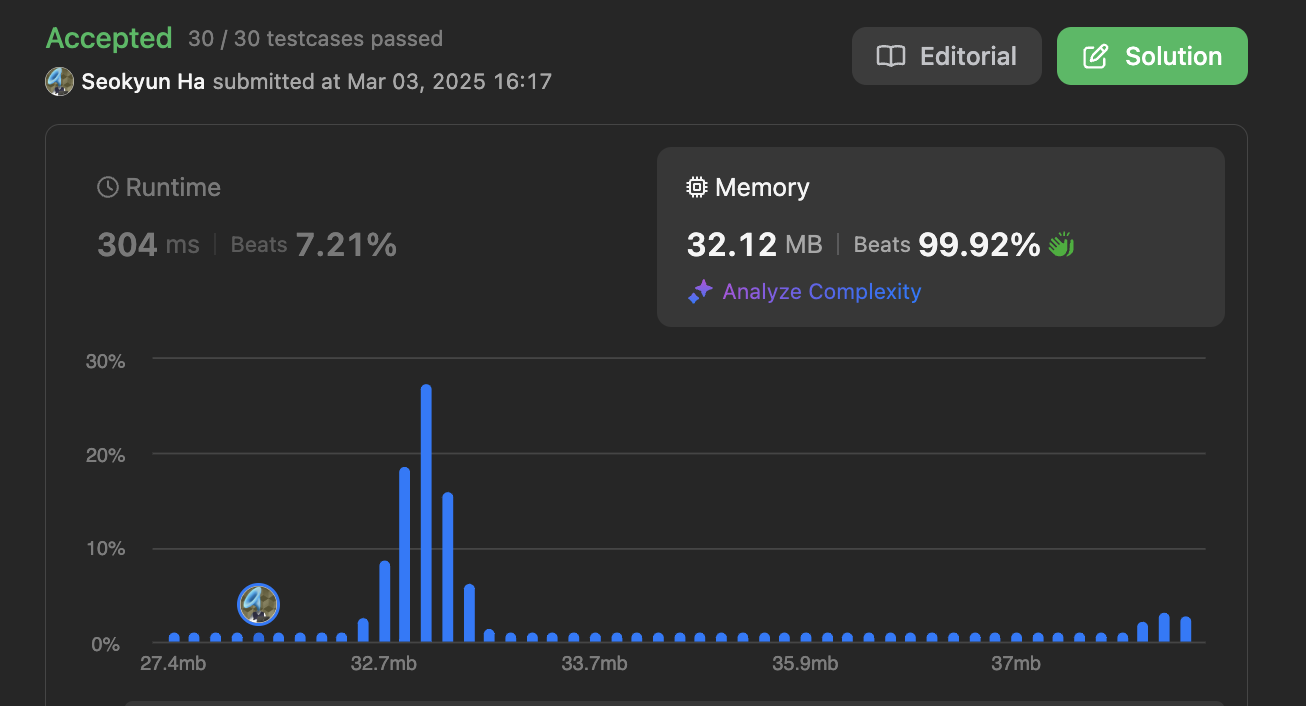
결과를 보면, 시간 복잡도는 그저그런 순위이지만, 메모리 사용량이 압도적으로 줄었습니다 ✌️ 시간을 조금 희생하면서 공간에 대한 이득을 본 것이죠!

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    @staticmethod
    def get_list_size(node: ListNode) -> int:
        i = 0
        while True:
            i += 1
            if node.next:
                node = node.next
            else:
                return i

    @staticmethod
    def get_next_nth_node(node: ListNode, cnt: int) -> ListNode:
        for _ in range(cnt):
            if node.next:
                node = node.next
        return node

    def merge(left_node, right_node) -> ListNode:
        new_head = None
        if left_node.val <= right_node.val:
            new_head = left_node
            left_node = left_node.next
        else:
            new_head = right_node
            right_node = right_node.next

        curr = new_head
        while left_node or right_node:
            if not left_node:
                curr.next = right_node
                right_node = right_node.next
            elif not right_node:
                curr.next = left_node
                left_node = left_node.next
            elif left_node.val <= right_node.val:
                curr.next = left_node
                left_node = left_node.next
            else:
                curr.next = right_node
                right_node = right_node.next
            curr = curr.next

        return new_head


    def sortList(self, head: Optional[ListNode]) -> Optional[ListNode]:
        if not head:
            return head

        if not head.next:
            return head

        sz = Solution.get_list_size(head)
        mid = sz // 2
        # print('sz: ', sz, 'mid: ', mid)

        l_list = head
        l_list_tail = Solution.get_next_nth_node(head, mid - 1)
        r_list = l_list_tail.next
        l_list_tail.next = None
        # print('l_head', l_list.val, 'r_head', r_list.val)

        l_list = self.sortList(l_list)
        r_list = self.sortList(r_list)

        return Solution.merge(l_list, r_list) # new head