Dijkstra’s Algorithm
2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :) 전체 포스트는 Algorithm 포스트에서 확인하실 수 있습니다.
<다익스트르라 알고리즘; Dijkstra’s Algorithm>은 그래프에서 최단 경로를 찾는 대표적인 알고리즘이다. 그래프의 모든 weight가 동일한 값을 가진다면, BFS를 통해서 최단 경로를 구할 수 있다. 또는 각 edge의 weight 값이 다르더라도, 아래와 같이 dummy node를 생성한다면, BFS로도 충분히 최단 경로를 얻을 수 있다.
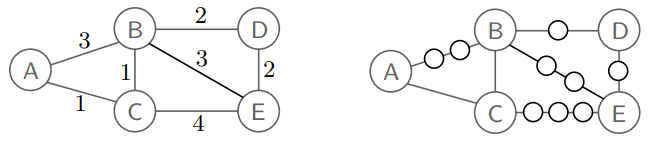
하지만, 만약 $\max w_i$의 값이 10,000일 정도로 정말 큰 값이라면, 우리는 dummy node를 생성하는 데에 너무 많은 overhead를 쓰게 된다.
Dijkstra’s Algorithm
BFS의 이런 문제를 해결하기 위해 <alarm clock algorithm>을 도입할 수 있다.
1. Set $\texttt{alaram}(s)=0$, and for all other nodes $v$, set $\texttt{alarm}(v)=\infty$.
2. Repeat until there’re no more alarms:
2.1. Say the next alarm rings at time $T$, for node $u$. Then, the distance from $s$ to $u$ is $T$.
2.2. For each neighbor $v$ of $u$, $\texttt{alarm}(v) = \min \left\{ \texttt{alarm}(v), T + \ell (u, v) \right\}$
위에서 제시된 <alarm clock algorithm>은 <우선순위 큐; priority queue>를 통해 쉽게 구현할 수 있다!
Algorithm: dijkstra($G$, $\ell$, $s$)
※ 주의: 그래프 $G$의 모든 edge는 positive edge여야 한다.
// initialization
for all $u \in V$ do
$\texttt{dist}(u) = \infty$
$\texttt{prev}(u) = \texttt{nil}$
end for
// construct heap
$\texttt{dist}(s) = 0$
$H = \texttt{makequeue}(V)$
// explore frontier!
while $H$ is not empty do
$u = \texttt{deletemin}(H)$
for all edges $(u, v) \in E$ do
if $\texttt{dist}(v) > \texttt{dist}(u) + \ell(u, v)$ then
$\texttt{dist}(v) = \texttt{dist}(u) + \ell(u, v)$
$\texttt{prev}(v) = u$
$\texttt{decreasekey}(H, v)$
end if
end for
end while
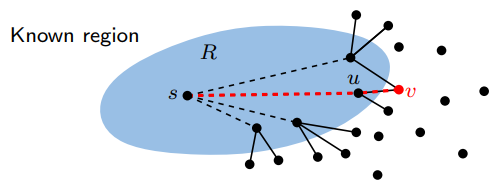
다익스트라 알고리즘은 Explored 영역에서 Frontier 영역을 탐색하고 확장하는 방식으로 동작한다.
간단하게 생각하면, shortest path로 안내하는 <shortest path tree>를 구축할 때, 이미 완성된 shortest path tree와 인접한 노드들인 Frontier를 살펴보며, SPT를 확장한다는 말이다. 이때, SPT growing rule은 현재의 heap에서 가장 작은 cost를 가지는 노드를 기준으로 확장을 한다는 것이다!
위와 같은 방식으로 접근하여 앞에서 소개한 방식의 동치인 알고리즘을 제시할 수도 있다.
Algorithm: dijkstra($G$, $\ell$, $s$)
// initialization
for all $u \in V$ do
$\texttt{dist}(u) = \infty$
$\texttt{prev}(u) = \texttt{nil}$
end for
// construct heap
$\texttt{dist}(s) = 0$
$R = \left\{ \right\}$ (the “known region”)
// explore frontier!
while $R \ne V$ do
Pick the node $v \notin R$ with smallest $\texttt{dist}$ value
Add $v$ to $R$
for all edges $(v, z) \in E$
if $\texttt{dist}(z) > \texttt{dist}(v) + \ell(v, z)$ then
$\texttt{dist}(z) = \texttt{dist}(v) + \ell(v, z)$
end if
end for
end while
Complexity
당연하게도 다익스트라 알고리즘은 BFS보다 더 느리다. 왜냐하면, Priority Queue의 연산이 들어가기 때문이다. (PQ의 연산은 기본 $\log_2 n$는 먹는다.)
다익스트라는 기본적으로 모든 노드를 살펴보기 때문에, 노드 갯수인 $\left| V \right|$번 만큼 PQ에 $\texttt{insertion}$ 하게 된다.
또, PQ를 비우기 위해 PQ에 넣은 노드를 $\texttt{deletemin}$으로 한번씩 모두 꺼내줘야 하기 때문에 $\left| V \right|$번 만큼 PQ에 $\texttt{deletemin}$ 하게 된다.
그리고 각 fronter point에서 노드와 연결된 모든 edge를 살펴보기 때문에 $\left| E \right|$번 만큼 $\texttt{decreasekey}$ 연산을 수행한다.
만약 Binary Heap로 구현된 PQ를 사용한다면,
- $\texttt{deletemin}$에 $O(\log \left| V \right|)$ 만큼의 비용이 들고,
- $\texttt{insert}$와 $\texttt{decreasekey}$는 $O(\log \left| V \right|)$ 만큼의 비용이 든다.
따라서, 전체 비용은
\[O(V \log V) + O((V + E) \log V) = O((V+E) \log V)\]PQ 또는 Heap을 Binary Heap이 아닌 다른 방식들, 예를 들면, <$d$-ary heap>, <Fibonacci heap> 등으로 구현해 시간을 더 줄일 수도 있다고 한다.
* 자세한 내용은 위키피디아의 해당 항목을 참고 👉 link
추가 해설
※ Note: Dijkstra’s Algorithm을 <UCS; Universal Cost Search>라고도 부른다.
Q. UCS는 정말 minimum cost path를 보장하는가?
→ 즉, PQ에서 $\texttt{pop}$되는 녀석은 그때의 $\texttt{PastCost}(s)$ minimum cost임을 보장한다.
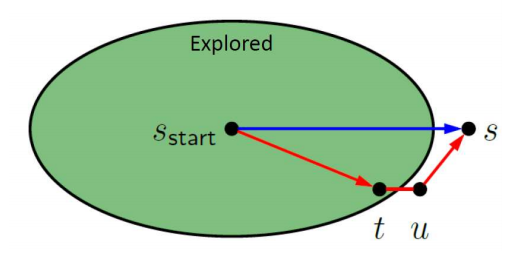
A. (귀류법) $s$가 PQ에서 $\texttt{pop}$될때, 그때의 $\texttt{PastCost}(s)$가 minimum cost가 아니라고 가정하자. 이것은 $s$ 이후에 $\texttt{pop}$되는 $u$라는 어떤 노드가 있고, $u \rightarrow s$로 가는 path가 minimum cost를 가짐을 의미한다.
하지만, PQ는 $\texttt{PastCost}(\cdot)$이 작은 순서대로 정렬하기 때문에 이후에 $\texttt{pop}$되는 $u$의 $\texttt{PastCost}(u)$는 $\texttt{PastCost}(s)$보다 클 것이다. 이것은 $\texttt{PastCost}(u) + \ell(u, s) < \texttt{PastCost}(s)$라는 $u$의 존재와 모순된다. 그래서 $u$를 거쳐 $s$로 가는 path는 절대 minimum cost path가 될 수 없다.
따라서 $s$가 $\texttt{pop}$된 때의 $\texttt{PastCost}(s)$보다 작은 minimum cost path는 존재할 수 없으므로 $s$가 $\texttt{pop}$될 때의 $\texttt{PastCost}(s)$가 minimum cost이다.
Q. 왜 UCS는 negative cost를 지원하지 않는가?
A. 만약 negative cost가 존재한다면, PQ를 이용해 min-cost tree를 만드는 과정에서 이미 탐색을 완료한 Explored 노드의 min-cost가 바뀔 수 있기 때문에 이미 구축한 min-cost tree를 무너뜨리게 된다. 이것은 앞선 명제에서 언급한 “이후에 $\texttt{pop}$되는 $u$의 $\texttt{PastCost}(u)$는 $\texttt{PastCost}(s)$보다 클 것이다.”라는 명제를 위반하는 것이고, 더이상 UCS의 correctness를 보장할 수 없다는 말이 된다.
<다익스트라 알고리즘>의 단점은 Negative Edge를 처리하지 못한다는 것이다. 이어지는 포스트에서는 Negative Edge를 처리하는 알고리즘인 <Bellman-Ford Algorithm>에 대해 살펴본다.
