Longest Increasing Subsequences
2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :)
<Longest Increasing Subsequence> 줄여서 <LIS> 문제는 sequence of numbers가 입력으로 들어올 때, 증가하는 부분수열(increasing subsequence) 중에서 가장 긴 부분수열을 찾는 문제다!
예를 들어 우리에게 아래와 같은 수열이 주어졌다고 하자.
이때, 증가하는 부분수열을 만들기 위해 가능한 모든 transition을 표시하면 아래와 같다!
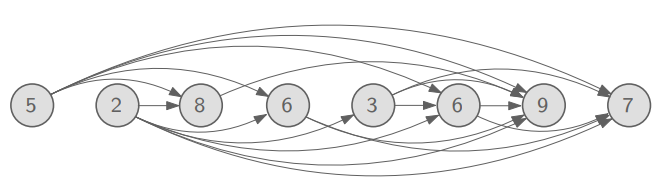
Directed Graph가 그려졌다!! 그런데, 좀 익숙하지 않은가? 바로 DAG다!!
사실 위의 상황을 그래프로 만든 후, 앞에서부터 BFS를 하면서 Longest Path를 찾아도 문제를 풀 순 있다. 그런데, DP는 조금 다른 방식으로 알고리즘을 제시한다!!
for $j=1, 2, \dots, n$
$L(j) = 1 + \max \{ L(i) : (i, j) \in E \}$
return $\max_j L(j)$
위의 알고리즘의 동작 방식을 생각해보면, 단순히 $O(N^2)$으로 해결할 수 있음을 알 수 있다!! 원래는 BFS로 풀면, $N\times O(N^2)$은 걸릴 문제를 $O(N^2)$로 해결할 수 있다니 놀랍지 않은가??
DP의 마법은 이제 시작이다. 이어지는 포스트에서는 LIS 보다 쪼오금 복잡한 방식으로 DP를 수행하는 <Edit Distance> 문제에 대해 살펴본다!!
추천 문제
p.s. 참고로 평범한 LIS 문제는 위의 DP보다 더 빠른 알고리즘이 존재한다!! $O(N \log N)$으로 동작하는 알고리즘으로, binary search를 활용한다. 자세한 내용이 궁금하면, 아래의 포스트를 참고하도록 하자.