Fourier Transform
2021-1학기, 대학에서 ‘데이터 마이닝’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :)
사실 정규 수업 때 배운 건 아니고, <Wavelet Transform> 부분의 수업을 이해하기 위해 개인적으로 정리한 포스트다.
Introduction to Fourier Transform
<푸리에 변환; Fourier Transform>은 신호(signal)에서 주파수를 분석하기 위해 사용하는 테크닉이다.
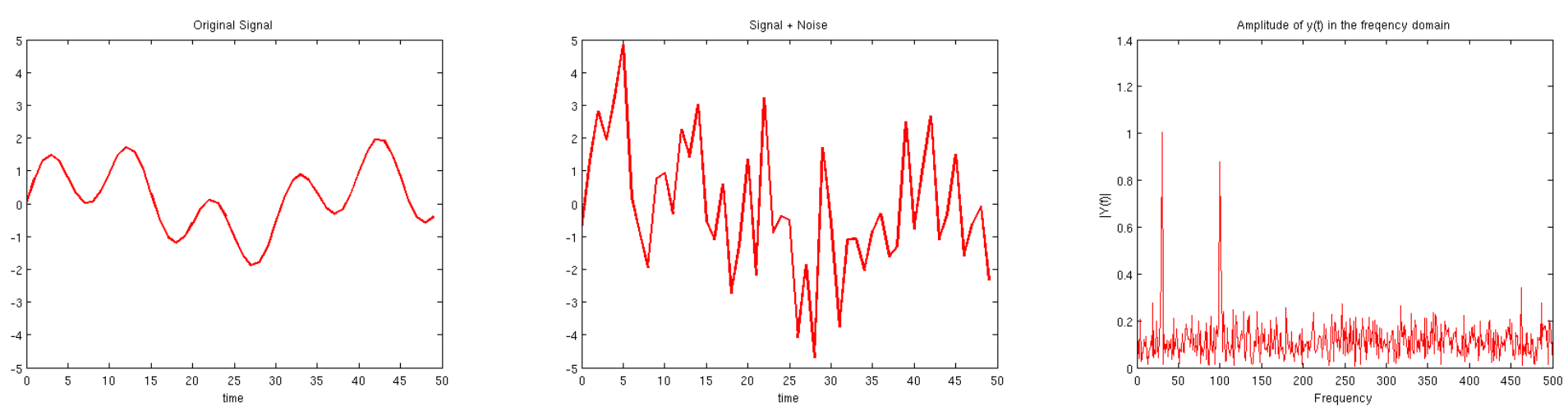
흔히 위와 같이 신호에 잡음(noise)가 섞여 있는 경우에, 신호를 복원하기 위해 사용한다. 이때, (signal + noise)를 오른쪽의 “주파수 공간“으로 변환하는 것을 <푸리에 변환>이라고 한다.
Fourier Transform
주기가 $2L$인 주기함수 $x(t)$를 아래와 같이 <푸리에 급수> 형태로 표현할 수 있다.
\[\begin{aligned} x(t) &= \sum_{-\infty}^{\infty} C_k \cdot e^{ik\pi t/L} \\ &\text{where} \\ C_n &= \frac{1}{2L} \int_{-L}^L x(t) e^{-in\pi t/L} \; dt \end{aligned}\]이때, 주기 $2L$에 대해서 극한을 취해 $L \rightarrow \infty$로 보낸다면, 이것은 함수 $x(t)$가 사실항 비주기 함수가 됨을 의미한다. 이는 곧 어떤 비주기 함수도 <푸리에 급수>를 통해 sinusoidal function으로 분해할 수 있다는 것을 말한다!
비주기 함수에서의 <푸리에 급수> 형태를 살펴보기 위해 <푸리에 급수>에 대한 식에 아래와 같이 극한을 취해보자.
\[\begin{aligned} \lim_{t\rightarrow\infty} x(t) &= \lim_{t\rightarrow\infty} \sum_{-\infty}^{\infty} C_k \cdot e^{ik\pi t/L} \\ &= \lim_{t\rightarrow\infty} \sum_{-\infty}^{\infty} \left[ \frac{1}{2L} \int_{-L}^L x(t) e^{-in\pi t/L} \; dt \right] \cdot e^{ik\pi t/L} \end{aligned}\]이때, 식을 약간 변형해서 $1/2L$을 식의 오른쪽 끝으로 보내자.
\[\lim_{t\rightarrow\infty} x(t) = \lim_{t\rightarrow\infty} \sum_{-\infty}^{\infty} \left[ \int_{-L}^L x(t) e^{-ik\pi t / L} \; dt \right] \cdot e^{ik\pi t / L} \cdot \frac{1}{2L}\]그러면, 위의 정적분의 극한에서 몇가지 기호를 아래와 같이 변환할 수 있다.
- $k/2L \rightarrow f$1 🔥
- $L \rightarrow \infty$
- $-L \rightarrow -\infty$
기호도 이에 맞춰 아래와 같이 바꿔주자.
\[\lim_{t\rightarrow\infty} x(t) = \sum_{-\infty}^{\infty} \left[ \int_{-\infty}^{\infty} x(t) e^{-i2\pi f t} \; dt \right] \cdot e^{i2\pi f t} \cdot \frac{1}{2L}\]여기에서 위의 식에서 계수에 대한 부분을 <푸리에 변환>이라고 한다!
\[X(f) = \int_{-\infty}^{\infty} x(t) e^{-i2\pi f t} \; dt\]이제 본래 식에 위의 <푸리에 변환>에 대한 식을 대입하면 아래와 같다.
\[\lim_{t\rightarrow\infty} x(t) = \sum_{-\infty}^{\infty} X(f) \cdot e^{i2\pi f t} \cdot \frac{1}{2L}\]이제, 정적분의 극한을 적분 형태로 바꿔줄 것이다. 위의 식에서 아래와 같이 변환해 식을 적분 형태로 바꾸자!
- $1/2L \rightarrow df$
- $\lim_{t\rightarrow\infty}$ 부분 역시 제거해주자.
끄-읕!! $\blacksquare$
식을 정리하면 아래와 같다.
\[\begin{aligned} x(t) &= \int_{-\infty}^{\infty} X(f) \cdot e^{i2\pi f t} \; df \\ &\text{where} \\ X(f) &= \int_{-\infty}^{\infty} x(t) \cdot e^{-i2\pi f t} \; dt \end{aligned}\]잘 보면 기존의 <푸리에 급수> 식에서 크게 변하지 않았고, 유도 과정 또한 극한만 잘 적용하면 되는 문제라서 꽤 쉬운 편이었다 ㅎㅎ
사실 위의 식은 <푸리에 역변환>에 대한 식이고, 우리가 “함수 $x(t)$의 푸리에 변환”이라고 부르는 부분은 $X(f)$다.
\[X(f) = \int_{-\infty}^{\infty} x(t) \cdot e^{-i2\pi f t} \; dt\]<푸리에 변환>과 <푸리에 역변환>에 대한 식을 함께 살펴보자.
1. 푸리에 변환
\[X(f) = \int_{-\infty}^{\infty} x(t) \cdot e^{-i2\pi f t} \; dt\]2. 푸리에 역변환
\[x(t) = \int_{-\infty}^{\infty} X(f) \cdot e^{i2\pi f t} \; df\]<푸리에 변환>과 <푸리에 역변환>에 대한 두 식이 아주 비슷하고 약간의 대칭적인 모습을 보인다 😲 $e^{-i2\pi f t}$와 $e^{i2\pi f t}$가 서로 “켤레복소수(complex conjugate)”인 점도 주목 할만 하다.
푸리에 변환의 의미
\[X(f) = \int_{-\infty}^{\infty} x(t) \cdot e^{-i2\pi f t} \; dt\]<푸리에 변환>에 대한 식을 잘 보면, 사실 <푸리에 변환>은 주파수가 $f$인 sinusoidal function과 함수 $x(t)$의 내적임을 알 수 있다.
\[X(f) = \left< x(t), \; e^{i2\pi f t}\right> = \int_{-\infty}^{\infty} x(t) \cdot (e^{i2\pi f t})^{*} \; dt = \int_{-\infty}^{\infty} x(t) \cdot e^{-i2\pi f t} \; dt\]글의 맨 처음에 우리가 <푸리에 변환>이 시그널을 “주파수 공간(frequency space)”로 변환하는 테크닉이라고 소개했는데, 이 변환하는 과정에서 사실 함수 $x(t)$를 frequency basis function $e^{i2\pi ft}$와 내적하는 과정을 통해 이루어지는 것이었다!!
이렇게 이해해보니 <푸리에 변환>이 더 직관적이고 쉬워 보이지 않는가?? ㅎㅎ 😆 <푸리에 역변환> 역시 $X(f)$에서 주파수를 고정하고 시간에 대한 time basis function $e^{-i2\pi ft}$와 내적하는 것에 불과하다.
reference
-
개인적으로 이 부분을 한번에 이해하기 힘들었다. 사실 조금 뒤에 나올 미소변화량 $df$가 자연스러움을 이해하면, 이 부분을 이해하는 것도 어렵지 않다. $1/2L$을 $df$로 정의하게 되면, $f$는 $k/2L$로 정의하는게 자연스럽다. 미소변화량인 $df$는 $d(k/2L) = (k+1)/2L - k/2L = 1/2L = df$로 유도할 수 있기 때문이다! ↩
