Network Flow
2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :) 전체 포스트는 Algorithm 포스트에서 확인하실 수 있습니다.
이번 포스트에서는 Network Flow 문제에 대한 개요와 Network Flow 문제의 핵심이 되는 정리인 “Max-Flow Min-Cut Theorem”에 대해 다룹니다. 실제 예제와 코드는 이어지는 포스트 Ford-Fulkerson & Edmons-Karp Algorithm를 참고해주세요! 😉
Introduction to Network Flow
<Network Flow> 문제는 아래와 같은 Directed Graph $G$에 대해 source $S$에서 sink $t$로 흘러가는 Flow의 合을 최대화 하는 문제다.
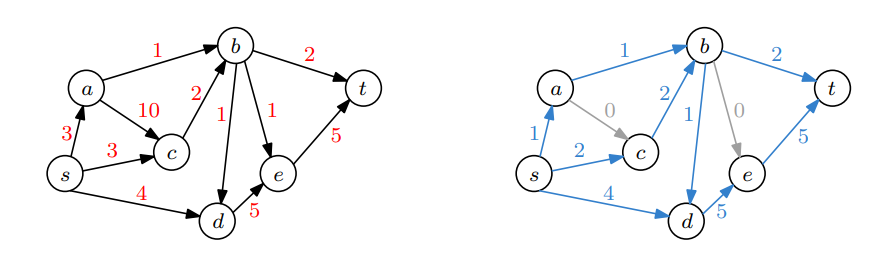
좀더 formal 하게 기술하면 아래와 같다.
For a directed graph $G = (V, E)$, we have two special nodes source $s$ and sink $t$. And each edges has capacity $c_e > 0$, respectively.
We want to send as much flow as possible from $s$ to $t$ s.t. $0 \le f_e \le c_e$ for all $e \in E$.
But for each node $u$, the flow must be conserved with $\displaystyle\sum_{(w, u) \in E} f_{wu} = \sum_{(u, z) \in E} f_{uz}$.
// node $u$에서 들어오는 양과 나가는 양이 같아야 한다.
Also the size of flow $\text{size}(f)$ should be
\[\text{size}(f) = \sum_{(s, u) \in E} f_{su} = \sum_{(v, t) \in E} f_{vt}\]위와 같이 기술된 <Network Flow> 문제를 살펴보면 정말 유량(Flow)에 대한 당연한 얘기들을 하고 있다는 것을 알 수 있다. 이런 당연한 얘기들이 전부 constraint가 된다는게 흠이지만…
Residual Network
<Networ Flow> 문제는 기존의 Graph $G$에서 <Residual Network>라는 그래프를 구축(construction) 하면서 해결할 수 있다! 😉 알고리즘이 한번에 이해 되지는 않으니 주의 깊게 살펴보자!
Find an $s-t$ path whose edges $(u, v)$ can be of two types:
1. $(u, v) \in E$ and $f_{uv} < c_{uv}$
2. $(v, u) \in E$ and $f_{vu} > 0$
예를 통해 위의 규칙을 이해해보자.
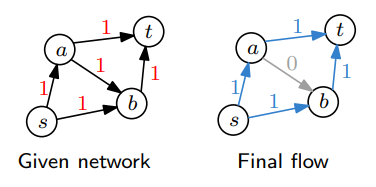
우리는 왼쪽의 그래프에서 시작해 오른쪽의 결과를 얻고자 한다.
먼저 첫 번째 규칙에 따르면 $s-t$ path는 $s \rightarrow a \rightarrow t$, $s \rightarrow b \rightarrow t$ 또는 $s \rightarrow a \rightarrow b \rightarrow t$의 경로를 찾을 수 있다. 여기서는 $s \rightarrow a \rightarrow b \rightarrow t$의 경로로 flow를 흘려보냈다고 하자.
기존의 방식에서는 가운데 $a \rightarrow b$ 방향으로 flow를 흘려보냈기 때문에 더이상 flow를 흘려보낼 경로가 존재하지 않는다. 그러나 두 번째 규칙을 적용하면, 추가로 flow를 흘려보낼 수 있다!!
두 번째 규칙을 적용하면 $s \rightarrow b \rightarrow a \rightarrow t$ 경로로 flow를 흘려보낼 수 있다! 이때, $b \rightarrow a$는 기존 그래프에는 없던 간선이지만, 두 번째 규칙에 의해 $f_{ab} = 1 > 0$이기 때문에 $(b, a) \in E$에 대한 edge를 사용할 수 있게 되었다!!
이제, 경로 $s \rightarrow a \rightarrow b \rightarrow t$와 $s \rightarrow b \rightarrow a \rightarrow t$를 종합하면 우리는 오른쪽의 결과를 얻게 되며, network의 최대 유량은 2라는 결과를 얻게 된다!
<Network Flow> 알고리즘에서는 위와 같은 과정을 좀더 편하게 다루기 위해, $s-t$ 경로를 찾는 매번의 과정에서 <Residual Graph> $G^f = (V, E^f)$라는 그래프를 갱신하며 사용한다. 우리는 Residual Graph $G^f$에서 Network Flow 문제를 해결함으로써 기존의 그래프 $G$의 Network Flow 문제를 해결할 수 있다! 즉 $G \equiv G^f$, $G$와 $G^f$가 동치인 셈이다! 😲
<Residual Graph> $G^f$에 대해 formal 하게 기술하면 아래와 같다.
During the algorithm, we maintain a residual graph $G^f = (V, E^f)$, which has two types of edges with residual capacities
\[c^f_{uv} = \begin{cases} c_{uv} - f_{uv} & \text{if} \; (u, v) \in E \; \text{and} \; f_{uv} < c_{uv} \\ f_{vu} & \text{if} \; (v, u) \in E \; \text{and} \; f_{vu} > 0 \; ( \equiv \text{$(u, v)$ is reverse edge}) \end{cases}\]<Network Flow> 문제를 <Residual Network>로 푸는 것은 사실 Linear Programming의 <Simplex Method>를 사용하는 것이라고 한다. 이에 대해서는 추후에 별도의 포스트에서 더 자세히 다루도록 하겠다 😉
Residual Flow는 자연스러운 접근인가?
Residual Graph $G^f$ 개념을 처음 배울 때는 간선에 유량 $f$가 흐르면 반대편에 $f$ 만큼의 capacity가 생긴다는 사실을 잘 이해하지 못했다. 그냥 ‘아, 그냥 테크닉인가 보구나’하고 받아들였다. 그러나 이 부분 때문에 Network Flow를 제대로 받아들이지 못 하고 계속 걷돌고 있었다. 이번 문단에서는 본인이 나중에 이해하게 된 Residual Flow를 잘 설명해보려고 한다.

다시 이름으로 돌아와보자. Given graph에서 $s \rightarrow a \rightarrow b \rightarrow t$의 경로로 flow를 흘려보내면 Residual Flow를 쓰지 않으면 더이상 문제를 해결할 수 없었다. Residual Flow를 적용하면 $b \rightarrow a$에 capacity $1$이 추가되어 $s \rightarrow b \rightarrow a \rightarrow t$가 가능해져 Final flow를 얻을 수 있다. 그런데 $b \rightarrow a$에 capacity $1$을 추가하는게 말이 되는 걸까?
놀랍게도 말이 된다! 다른 건 다 제거하고 $a \; – \; b$ 구간만 보자. $a \rightarrow b$로 1만큼의 유량이 흐른다고 하자. 그런데 이렇게 유량 1이 흐르는 상태에서 반대 방향 $a \leftarrow b$로 1만큼의 유량을 흘려보낸다면 두 유량은 상쇄되어 0이 될 것이다. residual flow는 바로 이것을 말한다. 이미 간선에 흐르는 flow $f_e$에 대해 그걸 상쇄하는 건 가능하다. 그래서 그걸 상쇄하는 양이 흐를 수 있도록 기존 그래프 $G$를 약간 수정하는 거다. $c_e’ = f_e$가 되도록 말이다!
이런 접근이 자연스럽다고 여기게 되는 점은 residual flow는 꼭 간선에 흐르는 flow 만큼만 생긴다는 것이다. 이것은 이미 흐르는 flow $f_e$보다 많은 residual flow가 흘러서 $f_e$가 음수가 되는 현상을 방지한다. 이 사실들을 이해한다면 residual flow는 꽤 자연스러운 접근이라고 깨닫게 될 것이다.
Optimality
위와 같은 접근법이 Maximum Flow를 보장하는지를 확인해보자! 설명의 편의를 위해 이미 Maximum Flow를 구한 Residual Graph를 사용하도록 하겠다.
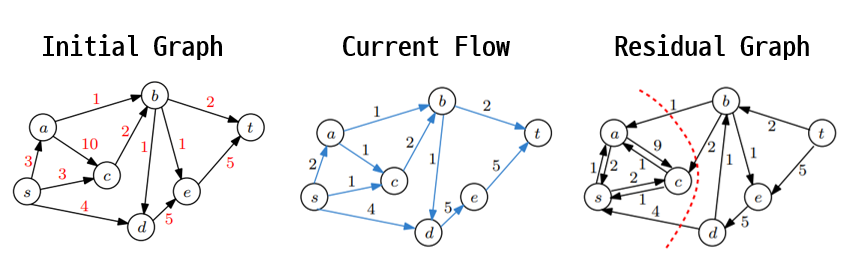
그래프 $G$를 $s$를 포함하는 $L = \{ s, a, c\}$, $t$를 포함하는 $R=\{ b, d, e, t\}$로 분할해보자. 이렇게 vertex set을 disjoint set $(L, R)$로 분할하는 것을 $(s, t)$-cut또는 간단하게 cut이라고 한다. 이때, $L-R$을 잇는 edge의 집합을 cut-set라고 하며, 이 cut-set의 capacity의 총합이 $(s, t)$-cut의 capacity가 된다. 사실 $s$와 $t$를 disjoint set으로 분할하는 가능한 cut은 정말 많다. 이때, minimum cut 줄여서 min-cut은 cut capacity가 최소가 되는 cut을 말한다.
$s \rightarrow t$ 방향으로 흐르는 모든 유량(flow)은 $L$에서 $R$을 지나야 한다. 그러므로 어떤 유량도 $L$과 $R$ 사이를 잇는 edge의 capacity 보다 큰 값을 가질 수 없다. 이것은 네트워크의 유량(flow)의 총합이 $(s, t)$-cut의 capacity를 넘을 수 없음을 의미한다.
Lemma 1.
Pick any $(s, t)$-cut $(L, R)$ and any flow $f$, then $\text{size}(f) \le \text{capacity}(L, R)$.
우리는 아직 $G$를 어떻게 분할해야 할지 정하지 않았다. 위의 명제는 그래프를 어떻게 분할하는지에 상관 없이 네트워크에 흐르는 전체 유량은 $\text{capacity}(L, R)$ 넘지 못한다, 즉 upper bound로 가진다를 말할 뿐이다.
이번에는 $(s, t)$-cut에 흐르는 flow에 대한 Lemma를 살펴보자.
Lemma 2.
For two vertex set $L$ and $R$, $v$ is an element of $R$. Remove $v$ from $R$ and place it in $S$, and now re-evaluate the flow of new cut $(L \cup \{ v\}, R \setminus \{ v \})$.
Let’s define two edge set $\text{In}(v)$ and $\text{Out}(v)$, they are incoming edges and outcoming edges of $v$ each. Then, by the conservation of flow:
\[\sum_{(u, v) \in \text{In}(v)} f(u, v) = \sum_{(v, w) \in \text{Out}(v)} f(v, w)\]Then, we partition $\text{In}(v)$ and $\text{Out}(v)$ based on where the end points of the edges fall as follows:
\[\begin{aligned} \text{In}(v)_L &= \left\{ (u, v) \in E \mid u \in L \right\} \\ \text{In}(v)_R &= \left\{ (u, v) \in E \mid u \in R \right\} \\ \text{Out}(v)_L &= \left\{ (v, w) \in E \mid w \in L \right\} \\ \text{Out}(v)_R &= \left\{ (v, w) \in E \mid w \in R \right\} \end{aligned}\]Moving $v$ into $L$ will result in losing $v$’s contribution to the original cut capacity, but also in gaining the capacity of the outgoing edges from $v$ thus:
\[\begin{aligned} &f(L \cup \{ v \}, R \setminus \{ v\}) \\ &= f(L, R) - \sum_{(u, v) \in \text{In}(v)_L} f(u, v) + \sum_{(v, w) \in \text{Out}(v)_L} f(v, w) - \sum_{(u, v) \in \text{In}(v)_R} f(u, v) + \sum_{(v, w) \in \text{Out}(v)_R} f(v, w) \\ &= f(L, R) - \cancel{\left(\sum_{(u, v) \in \text{In}(v)} f(u, v)\right)} + \cancel{\left(\sum_{(v, w) \in \text{Out}(v)} f(v, w)\right)} \\ &= f(L, R) \end{aligned}\]위의 결과는 어떤 cut을 잡든 상관없이 Network에 흐르는 flow의 최종값은 모두 동일하다고 말한다! 그래서 이 flow의 최종값을 value of flow, $\text{val}(f)$라고 부르겠다.
\[\text{val}(f) = f(L, R) = f(\{s\}, V \setminus \{s\}) = \sum_{(s, u) \in E} f(s, u)\]이 사실을 바탕으로 Lemma 1을 다시 쓰면 아래와 같다.
\[\text{val}(f) \le \text{capacity}(L, R)\]아직 포스트에서는 안 다뤘지만 Ford-Fulkerson을 수행하며 Residual Graph $G^f$를 얻었다고 해보자. 그리고 그때의 final flow를 $f$라고 하자. 그렇다면 그래프 $G^f$ 아래에서 source $s$는 더이상 sink $t$로 reachable 하지 않을 것이다.
$L$을 노드 $s$에서 reachable한 노드의 집합으로 설정하고, $R$은 $R = V - L$로 설정하자. 그러면 final flow $f$에 대해 아래가 성립한다!
Lemma 3.
For the residual graph $G^f$ driven by Ford-Fulkerson(simplex method), the following holds
\[\text{size}(f) = \text{capacity}(L, R)\]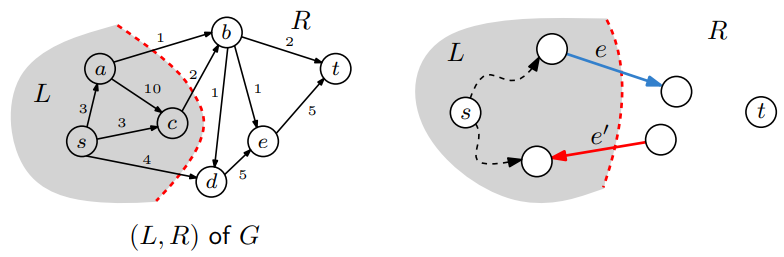
Ford-Fulkerson으로 유도되는 $(L, R)$ 분할에 대해 $\text{size}(f) = \text{capacity}(L, R)$가 성립함을 증명해보자.
먼저 $G^f$의 $L \rightarrow R$ 방향의 edge들을 살펴보자. 이런 edge에 대해서는 $f_e = c_e$로 full capacity 만큼의 flow가 흐른다. ($f_e \ne c_e$라면 flow를 더 흘려보낼 수 있기 때문에 final flow라는 가정을 위배한다.)
다음으로 $G^f$의 $L \leftarrow R$ 방향의 edge들을 살펴보자. 이런 edge에 대해서는 flow가 전혀 흐르지 않는 $f_{e’} = 0$이 된다. (만약 $f_{e’} \ne 0$라면 $f_{e’}$ 만큼 반대 방향으로 capacity가 생긴다. 이것을 따라 flow를 더 흘려보낼 수 있기 때문에 final flow 가정을 위배한다.)
따라서, Ford-Fulkerson으로 유래되는 $(L, R)$ 분할 아래에서는 $\text{size}(f)$가 정확히 $L \rightarrow R$ 방향의 capacity 만큼 흐른다! $\blacksquare$
그렇다면 Network Flow 문제의 목표인 Max-Flow를 달성하기 위해서는 어떤 $(s, t)$-cut을 잡아야 할까? 아래의 명제는 Max-Flow를 보장하는 $(s, t)$-cut에 대해 기술하고 있다.
Theorem. Max-flow min-cut theorem (MFMC)
The size of the maximum flow in a network equals the capacity of the smallest $(s, t)$-cut1.
또는 이렇게 표현할 수도 있다.
The following statements are equivalent.
- $f$ is maximized.
- $G^f$ has no augmenting paths.
- There exists a cut $(L, R)$ such that $\text{capacity}(L, R) = \text{size}(f)$
이 <MFMC Theorem>이 무엇을 의미하는지 살펴보자. Lemma 1, 2를 종합해 얻은 결론은 어떤 cut $(L, R)$을 잡든 그때의 capacity는 $\text{val}(f)$보다 크거나 같다이다. <MFMC Theorem>은 capacity가 최소가 되는, 즉 $\text{capacity}(L, R) = \text{val}(f)$가 되는 $(L, R)$ cut이 존재하지만, 그것은 오직 $\text{val}(f)$가 네트워크의 maximum flow일 때만 성립함을 말한다! (즉, $(3) \implies (1)$라는 말이다.)
MFMC Theorem이 기술하는 3가지 명제가 서로 Equivalent 함을 증명해보자. 증명 순서는 $(1) \implies (2)$, $(2) \implies (3)$, $(3) \implies (1)$ 순서로 진행한다.
1. $(1) \implies (2)$
Let $f$ be a max flow, and suppose $G^f$ still has an augmenting path $\mathcal{P}$ (귀류법). Then we can increase $\text{val}(f)$ by augmenting along the path $\mathcal{P}$. This contradicting the maximality of $f$.
$\therefore$ When the $f$ is maximized, $G^f$ should have no augmenting paths.
2. $(2) \implies (3)$
Suppose $G^f$ has no augmenting paths. Then we can easily construct a cut $(L, R)$ s.t. $\text{capacity}(L, R) = \text{val}(f)$ by the following way: Let $L$ denote the set of vertices reachable from $s$ and for a vertex $v$ if there is an augmenting path from $s$, then $v \in S$. Since $G^f$ has no augmenting $s-t$ path, we know that $t \not\in S$. And let $R$ be the $R = V \setminus L$, then $t \in R$, and this $(L, R)$ is a valid $s-t$ cut. Then, the capacity of $(L, R)$ is exactly the $f$ of the $G^f$. If not, then there’s more capacity to flow through $L$ to $R$, and it means $G^f$ has an augmenting path! (귀류법!)
3. $(3) \implies (1)$
Let $(L, R)$ be a cut with $\text{capacity}(L, R) = \text{val}(f)$, and let $f’$ be a maximum flow in $G$, so $\text{val}(f) \le \text{val}(f’)$. Since $\text{val}(f) = \text{capaicty}(L, R)$, then $\text{capacity}(L, R) \le \text{val}(f’)$. However, by the Lemma 1 $\text{val}(f’) \le \text{capacity}(L, R)$.
$\therefore$ $\text{val}(f’) = \text{capacity}(L, R) = \text{val}(f)$. This means the $f$ is the maximum flow!!
$\blacksquare$
이렇게 Residual Graph $G^f$를 구축하며 Maximum Flow를 찾는 알고리즘으로 <Ford-Fulkerson Algorithm>과 <Edmonds-Karp Algorithm>이 있는데 위의 <MFMC Theorem>은 $(2) \implies (1)$을 보장하기 때문에 Residual Graph $G^f$에서 augmenting path가 더이상 없는 그때 Maximum Flow를 얻을 수 있게 된다.
맺음말
이번 포스트에서는 <Network Flow> 문제란 무엇인지 그리고 Maximum Flow를 찾는 접근법과 그 방법의 Optimality를 살펴봤다. 아직 <Network Flow> 문제에 대해서는 아직 다뤄야 할 내용들이 많이 남아있다. 남은 부분들은 이어지는 Ford-Fulkerson & Edmons-Karp Algorithm 포스트에서 이어서 다루도록 하겠다.
references
- CS Toronto: “Network Flows: The Max Flow/Min Cut Theorem”
- Minimum Cut on a Graph Using a Maximum Flow Algorithm
- Wikipedia
-
smallest $(s, t)$-cut, 또는 “min-cut“이라는 개념이 등장한다. 이것은 그래프에서 가능한 모든 $(s, t)$-cut 중 capacity가 가장 작은 cut을 의미한다. ↩
