Ford-Fulkerson Algorithm & Edmons-Karp Algorithm

2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :) 전체 포스트는 Algorithm 포스트에서 확인하실 수 있습니다.

이번 포스트는 Network Flow 포스트의 후속 포스트입니다. Network Flow 문제의 핵심이 되는 정리인 <Max-Flow Min-Cut Theorem>에 대해 궁금하다면 이전 포스트를 참고해주세요! 😉

이번 포스트의 코드는 백준 6086번: 최대 유량 문제를 기준으로 작성되었습니다 👨‍💻

---

Network Flow 포스트에서 어떻게 Max Flow를 구할지 <Max-Flow Min-Cut Theorem>을 통해 살펴보았다. 이번 포스트에서는 Residual Graph를 사용하는 해당 알고리즘을 직접 구현해본다.

---

Ford-Fulkerson Algorithm

사실 Network Flow 포스트에서 설명한 Max-Flow를 찾는 방법을 코드로 구현한 것에 불과하다. 큰 범주로 봤을 때는 Brute Force Algorithm에 속한다.

1. source에서 sink로 가는 유량을 보낼 수 있는 경로 $p$를 하나 찾는다. DFS 또는 BFS를 이용하면 된다.

2. 찾아낸 경로 $p$로 보낼 수 있는 최대한의 유량을 구한다. 최대한의 유량은 경로 $p$를 탐색(traversal)하며 가장 작은 남은 capacity가 된다.

3. 찾아낸 경로 $p$에 최대 유량을 실제로 흘려보낸다. 이 과정에서 순방향은 유량을 추가하고, 역방향은 유량은 뺀다.

예를 들어 찾아낸 경로 $p$가 $a \rightarrow b \rightarrow c$라면,

// 순방향
f(a, b) += flow
f(b, c) += flow

// 역방향
f(b, a) -= flow
f(c, b) -= flow

주목할 점은 [3.] 과정에서 역방향을 처리할 때인데, 만약 $f(b, a) = 0$이었다면 $f(b, a) < 0$로 음수가 된다. 그런데 이런 음수 유량을 흘려보내는 것은 가능한데, $f(b, a)$의 capacity는 $c(b, a) = 0$이므로 결국 $f(b, a) < 0 = c(b, a)$로 유량에 대한 법칙을 전혀 깨뜨리지 않는다!

코드로 작성하기 전에 손으로 이 알고리즘을 따라가보자. 이 부분은 좋은 자료가 있어서 해당 자료로 대체하겠다. 🙏 손으로 푸는 Ford-Fulkerson Algorithm

이제 코드로 살펴보자.

✨ Tip: 이 문제의 경우 그래프를 Adjacency List 보다는 Adjacency Matrix로 표현하는게 알고리즘을 짜기 훨씬 편해진다! 😉

먼저 문제의 입력을 보면, 노드가 Alphabet 대소문자로 들어온다. 본인은 소문자로도 들어온다는 걸 나중에 깨달았다 😱 입력을 정규화하기 위해선 'A'로 빼주면 된다. 그러면 노드는 [A-Z]: [0, 26], [a-z]: [32, 57]의 번호를 갖게 된다.

우리는 int capacity[][]라는 배열에 파이프에 흐를 수 있는 유량의 capacity를 기록한다. 그래서 입력을 통해 Graph를 구축하면 아래와 같다.

#define MAX 80

int capacity[MAX][MAX];

for (int i = 0; i < N; i++) {
  char s, e;
  int c;
  cin >> s >> e >> c;
  capacity[s - 'A'][e - 'A'] += c;
  capacity[e - 'A'][s - 'A'] += c;
}

이제 준비는 끝났고, 본격적으로 <\Ford-Fulkerson Algorithm>을 구현해보자.

long long FordFulkerson(int source, int sink) {
  long long ret = 0;

  // find path and update residual graph
  while (1) {
    ...
    // dfs
    while (!s.empty()) {
      ...
    }

    // escape: no possible path
    if (Prev[sink] == -1) break;

    // find possible max-flow

    // flow the max-flow

    total_flow += flow;
  }

  return total_flow;
}

먼저 dfs 구현 부분을 살펴보자.

  int Prev[MAX];
  fill(Prev, Prev + MAX, -1);
  Prev[source] = source;

  stack<int> s;
  s.push(source);

  // dfs
  while (!s.empty()) {
    int curr = s.top();
    s.pop();

    if(curr == sink) break;

    for (int i = 0; i < MAX; i++) {
      if (Prev[i] == -1 && capacity[curr][i] > 0) {
        s.push(i);
        Prev[i] = curr;
      }
    }
  }

  // escape: no possible path
  if (Prev[sink] == -1) break;

stack<int>를 이용해 DFS를 구현했으며, Prev[]에 path history를 기록한다. 만약 sink에 도달했다면, 그래프 탐색을 종료한다. 만약 sink에 도달하지 못 했다면 즉 sink로 가는 경로를 찾지 못 했다면, Prev[sink]의 값이 갱신되지 않으므로 Prev[sink] == -1이 된다. 이 경우라면, 알고리즘을 종료한다.

사실 위의 알고리즘은 아래와 같이 쵸큼 개선할 수 있다.

  int Prev[MAX];
  fill(Prev, Prev + MAX, -1);
  Prev[source] = source;

  stack<int> s;
  s.push(source);

  // dfs
  while (!s.empty()) {
    int curr = s.top();
    s.pop();

    for (int i = 0; i < MAX; i++) {
      if (Prev[i] == -1 && capacity[curr][i] > 0) {
        s.push(i);
        Prev[i] = curr;

        if (i == sink) break;
      }
    }

    if (Prev[sink] != -1) break;
  }

  // escape: no possible path
  if (Prev[sink] == -1) break;

다만 처음의 코드처럼 구현해도 통과하기 때문에 크게 신경쓰지는 말자.

다음은 찾은 경로를 이용해 그래프에 흘릴 유량을 찾아야 한다. 이것은 아래의 코드로 수행할 수 있다.

  // find possible max-flow
  int flow = INT_MAX;
  for (int v = sink; v != source; v = Prev[v]) {
    flow = min(flow, capacity[Prev[v]][v]);
  }

for (int v = sink; v != source; v = Prev[v]) 패턴은 그래프 탐색에서 경로를 재구성 할 때 자주 쓰는 테크닉이므로 숙지 하도록 하자. 🙌

다음은 경로에 유량 flow를 흐르게 하는 작업이다. 마찬가지로 경로를 재탐색하며 유량을 흘려보내면 된다.

  // flow the max-flow
  for (int v = sink; v != source; v = Prev[v]) {
    capacity[Prev[v]][v] -= flow;
    capacity[v][Prev[v]] += flow;
  }

  // update total flow!
  total_flow += flow;

이때, 역방향으로는 capacity가 늘어난다는 사실에 유의하자.

시간 복잡도

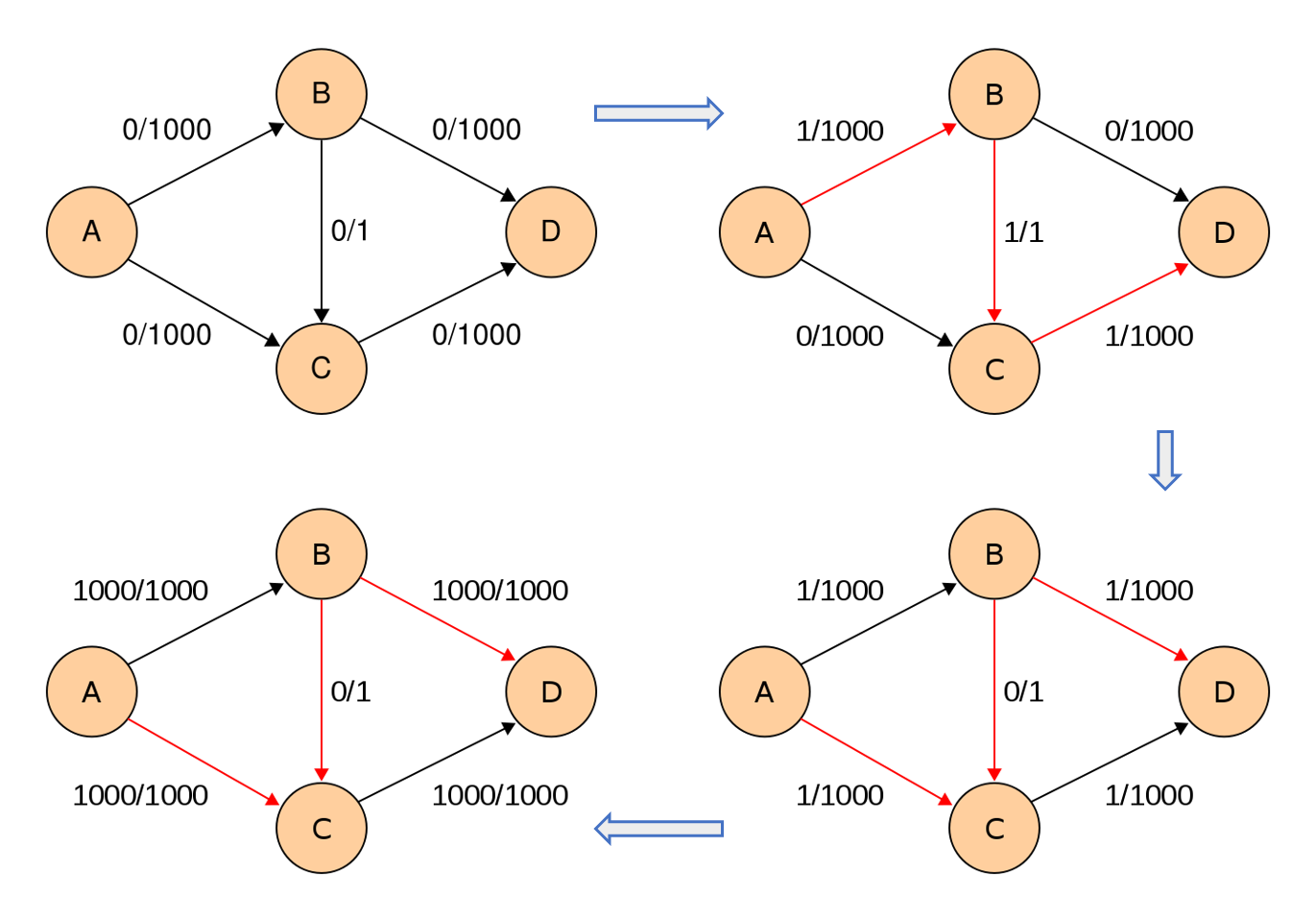
위의 그림은 <Ford-Fulkerson Algorithm>에서 최악의 상황의 예시이다. DFS로 경로를 찾는 매 시행마다 용량 1의 가운데 간선을 지난다고 하자. 그러면 용량 1,000을 채우기 위해 1,000은 iteration을 수행해야 한다. 이것은 DFS로 경로를 탐색하는 <Ford-Fulkerson Algorithm>의 한계이다 😥

위의 상황을 바탕으로 <Ford-Fulkerson Algorithm>의 시간 복잡도를 유도해보자. 그래프 $G_f$에서 최대 용량이 $f_{\max}$라고 하자. 한번의 DFS 탐색으로 흘릴 수 있는 유량의 최솟값은 1이므로 총 $f_{\max}$번의 DFS를 수행해야 한다. 이때, DFS의 시간복잡도가 $O(V + E)$이므로, <Ford-Fulkerson Algorithm>은 $O((V + E) f_{\max})$ 만큼의 시간복잡도를 가진다! 만약 정점의 갯수 $V$가 무시할 만큼 적다면 $O(E \cdot f_{\max})$라고 적기도 한다.

---

Edmonds-Karp Algorithm

앞선 <Ford-Fulkerson Algorithm>의 코드에서는 DFS를 통해 문제를 해결했다. 이때, 간선을 찾는 과정을 BFS로 수행한다면, <Edmonds-Karp Algorithm>이 된다!

<Edmonds-Karp Algorithm>은 기존 <Ford-Fulkerson Algorithm>이 최대 용량 $f_{\max}$가 큰 경우에 잘 동작하지 못한다는 점 때문에 제시된 알고리즘이다. 그런데 DFS에서 BFS로 바꾸면 무엇이 달라지는 걸까?

다시 위의 예제를 통해 살펴보자.

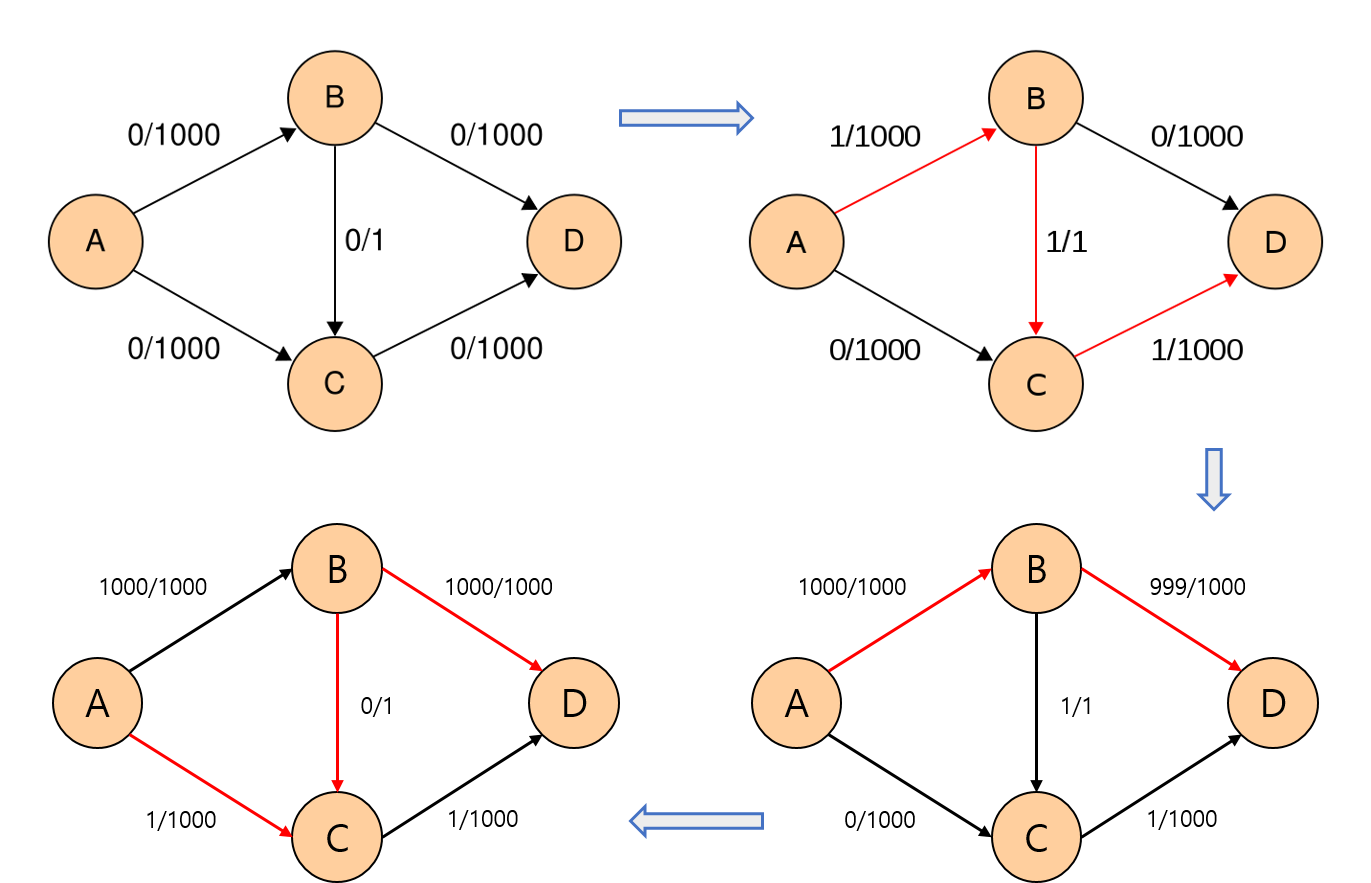
일단 맨처음에는 A - B - C - D의 경로로 유량이 흘렀다고 하자. 그 다음에 흐를 유량을 살펴보면,

1. 방문: [A], 큐: [B, C]
2. 방문: [A, B], 큐: [D] (B -> C는 이미 용량이 다 찼기 때문에 도달할 수 없다)
3. 방문: [A, B, D], 큐: []
4. 999만큼의 유량을 흘려보낸다.

이 과정을 반복하면 기존의 <Ford-Fulkerson Algorithm> 보다 훨씬 적은 iteration으로 총유량을 구할 수 있다.

<Edmonds-Karp Algorithm>은 flow의 값보다는 edge $E$에 더 영향을 받게 된다. 자세한 증명은 구사과님의 블로그를 통해 살펴보자 😉 나중에 정리하겠습니다…

결론은 <Edmonds-Karp Algorithm>이 $O(VE^2)$의 시간복잡도를 가진다!!

---

이것으로 네트워크 플로우 문제의 기본적인 두 알고리즘인 <Ford-Fulkerson Algorithm>과 <Edmonds-Karp Algorithm>을 살펴보았다. 두 알고리즘의 시간복잡도가 다르기 때문에 상황에 맞게 적절하게 선택해 사용하면 된다.

다음 포스트로는 네트워크 플로우를 이용해 해결할 수 있는 문제들에 대해 다룬다. 대표적인 문제로 <Bipartite Matching; 이분 매칭>과 네트워크 플로우에 제약(constraint)를 추가한 버전의 문제들을 살펴볼 예정이다 🙌

👉 Bipartite Matching

---

references

• 네트워크 유량(Network Flow)