Clustering of Maximum Spacing

2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :)

Kruskal’s Algorithm & Prim’s Algorithm에서 이어지는 포스트입니다.

---

<clustering>이란 주어진 $n$개의 대상을 서로 관련있는 것끼리 묶어 그룹화 하는 것을 말한다. 그래서 $k$-clustering이라 하면 $n$개 대상을 $k$개의 non-empty group으로 분할하는 것을 말한다.

그런데 어떤 clustering이 좋은 clustering일까? 보통은 관련 있는 것끼리는 가깝게 또 관련 없는 것끼리는 멀게 하는 clustering을 ‘좋은 clustering’이라고 한다. 이 ‘관련됨(coherence) 를 수치적으로 표현하기 위해서 <distance function>과 <spacing>이라는 개념이 등장한다.

<distance function>은 두 물체 사이의 거리를 측정하는 함수이다. 우리는 거리가 가까울 수록 coherent 하다고 판단한다. <distance function>으로는 Euclide distance나 $L_1$ distance 등이 대표적이다.

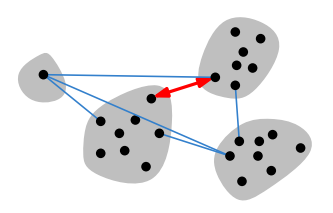
우리는 두 클러스터 사이에서도 거리를 매길 수 있는데, 이것을 cluster distance라고 하자. 이것은 두 클러스터 $C_1$, $C_2$에 각각 속하는 두 점에 대해 거리를 측정했을 때 가장 가까운 거리를 의미한다. 수식으로 적으면

\[\text{cluster dist}(C_1, C_2) = \min_{p_i, \; p_j} \, \text{dist}(p_i, p_j) \quad \text{where} \; p_i \in C_1, \; p_j \in C_2\]

이제 <spacing>을 정의해보자. <spacing>은 클러스터 사이의 cluster distance 중 가장 작은 distance를 말한다.

\[\text{spacing} = \min_{C_a, \, C_b} \; \text{cluster dist} (C_a, C_b)\]

다시 본론으로 돌아와서 ‘좋은 clustering’이란 무엇일까? 우리는 이것을 가능한 모든 $k$-clustering 중에서 maximum spacing을 가지는 cluster를 가장 좋은 clustering이라고 정할 것이다. 이것이 이번 포스트의 주제 “clustering of max. spacing“이다 👏

---

그렇담 “clustering of max. spacing“를 어떻게 찾을 수 있을까? Brute Force하게 접근한다면 당연히 조합 폭발을 경험할 것이다. 이때, 좋은 정리가 있는데 MST에서 가장 비싼 간선 $k-1$개를 삭제하면 $k$-clustering of max. spacing을 얻을 수 있다는 것이다!

Theorem.

Let $C^{*}$ denote the clustering $C_1^{*}, …, C_k^{*}$ formed by delete the $k-1$ most expensive edges of a MST. Then, $C^{*}$ is a $k$-clustering of max. spacing.

proof. (귀류법)

clustering $C^{*}$의 spacing $d^{*}$는 MST의 $(k-1)$번째로 비싼 간선일 것이다. 우리는 optimal clustering $C$가 있어 그 때의 spacing이 $d \ge d^{*}$라고 하자.

$C^{*}$의 clustering 중 하나인 $C_r^{*}$에 속한 두 점 $p_i$, $p_j$에 대해 살펴보자. 그런데 이 두 점이 $C$에서는 $C_s$, $C_t$에 속해 서로 분리된 상태라고 하자. 즉, $p_i \in C_s$, $p_j \in C_t$인 것이다.

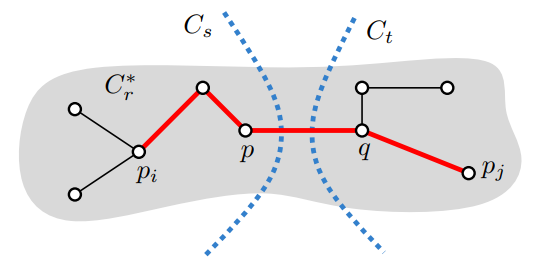
$C_r^{*}$ 위에서 $p_i$에서 $p_j$로 가는 경로를 생각해보자. 이때 중간의 어떤 간선 $(p, q)$는 $C$에서의 두 클러스터 $C_s$, $C_r$를 가르는 clustrer distance가 될 것이다. $p_i \rightarrow p_j$ 경로의 모든 간선은 MST의 정의에 따라 $(k-1)$번째 간선인 $d^{*}$의 길이보다는 작을 것이다. 따라서

\[\left| pq \right| \le d^{*}\]

어라! $C$을 정의할 때 spacing $d$가 $d \ge d^{*}$라고 정의했다. 그런데 $C$에 알고보니 $\left| pq \right| \le d^{*}$인 cluster distance $\left| pq \right|$가 존재했다. 이것은 곧 $d > d^{*}$가 불가능함을 의미한다. 따라서 $d = d^{*}$이므로 MST로부터 유도한 clustering $C^{*}$은 clustering of max. spacing이다! $\blacksquare$

---

이것으로 정규수업에서 다룬 모든 <Greedy Algorithm> 문제를 살펴보았다. 👏