Kruskal’s Algorithm & Prim’s Algorithm
2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :) 전체 포스트는 Algorithm 포스트에서 확인하실 수 있습니다.
MST는 weighted undirected graph $G=(V, E, W)$가 입력으로 들어올 때, 아래의 식을 만족하는 tree $T=(V, E’)$를 출력하는 알고리즘이다.
\[\underset{E'}{\text{argmin}} \sum_{e\in E'} w_e\]Kruskal’s Algorithm
<Kruskal’s Algorithm>은 empty graph에서 시작해 아래의 순서대로 Greedy 방식으로 edge를 선택하는 알고리즘이다.
남은 edge 중에 가장 light한 edge를 그래프에 추가한다. 단, edge를 추가했을 때, 그래프에서 cycle이 생기지 않아야 한다.

크루스칼 알고리즘의 correctness는 <cut property>에 의해 보장된다.
Theorem. Cut Property
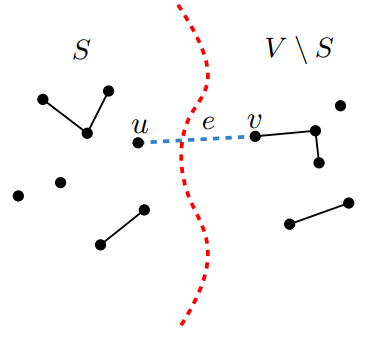
Supp. edges in $X \subset E$ are part of a MST $T$ of $G = (V, E)$.
Pick any subset of nodes $S$ for which no edge in $X$ crosses btw $S$ and $V\setminus S$,
and let $e$ be the lighstest edge across this partition.
Then $X \cup \{ e \}$ is part of some MST.
해설을 좀 하자면, $X$가 MST $T$의 부분집합이라고 하자. 이때, 이 $X$에 단 하나의 edge를 추가했을 때에도 여전히 MST $T$의 부분집합이 되게 만들고자 한다. 그러면, $X$의 모든 edge가 cross 하지 않도록 집합 $S$, $V \setminus S$를 잡았을 때, 두 집합을 가로지르는 edge 중 가장 light한 edge $e$를 선택해 $X$에 추가한다면, $X \cup \{e\}$가 여전히 MST의 부분집합이 된다는 정리이다.
Proof.
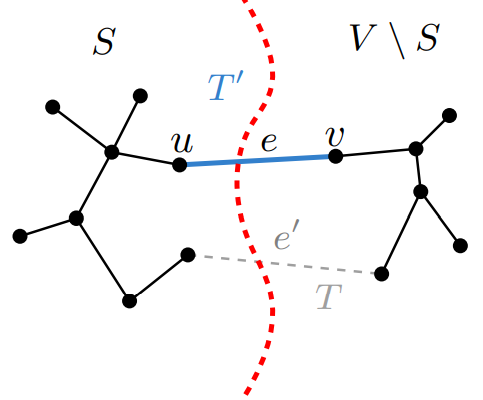
(귀류법) Assume $e = (u, v) \notin T$.
[1] 이때의 $e$는 위에서 언급한 $S$, $V\setminus S$를 잇는 가장 light한 edge다.
[2] 이때의 $T$는 true MST $T$를 의미한다.
We can construct a different MST $T’$ containing $X \cup \{ e \}$ by altering $T$ slightly.
$u$ and $v$ are connected by a path in $T$ which contains an edge $e’$ crossing $S$ and $V\setminus S$.
Construct a new tree $T’$ from $T$ by removing $e’$ and adding $e$.
Then, $T’$ is a spanning tree with $\texttt{cost}(T’) \le \texttt{cost}(T)$ (왜냐하면, $w_e \le w_{e’}$이기 때문.) 이것은 ST $T$가 MST라는 사실에 모순이다. 따라서, 처음에 가정한 $e = (u, v) \notin T$는 거짓이다.
따라서, $S$, $V\setminus S$를 연결할 때, the lightest edge $e$를 추가하는 것이 실제로 MST가 됨이 보장된다.
<Kruskal Algorithm>은 <set> 자료형을 사용해 쉽게 구현할 수 있다! 🤩
Algorithm: Kruskal($G$, $w$)
($G = (V, E)$ is a connected undirected graph with edge weights $w_e$.)
// initialization
for all $u \in V$ do
$\texttt{makeset}(u)$
end for
// construct empty MST
$X = \{ \}$
Sort the edges $E$ by weight.
// greedy process!
for all edges $\{ u, v\} \in E$, in increasing order of weight
if $\texttt{find}(u) \ne \texttt{find}(v)$ // cycle check!
add edge $\{u, v\}$ to $X$
$\texttt{union}(u, v)$ // merge two sets!
end if
end for
시간복잡도를 살펴보면,
- Weight에 따라 정렬: $O(E \log E)$
- $\texttt{makeset}$: $V$ 번
- $\texttt{find}$: $E$ 번
- $\texttt{union}$: $V-1$ 번
$\texttt{makeset}$, $\texttt{find}$, $\texttt{union}$ 연산에 대한 시간복잡도는 추후에 Disjoint Set 포스트에서 살펴보겠다.
Prim’s Algorithm
<Prim’s Algorithm>으로도 MST를 얻을 수 있다. 이 알고리즘의 아이디어도 아주 간단하다!
<Prim’s Algorithm>은 그래프 $G$에서 가장 light한 edge를 선택하며, intermediate MST $X$를 grow 하는 알고리즘이다. 이때, 크루스컬 때와 마찬가지로 선택한 edge로 인해 cycle이 형성되어서는 안 된다.
Algorithm: Prime($G$, $w$)
($G = (V, E)$ is a connected undirected graph with edge weights $w_e$.)
// initialization
for all $u \in V$
$\texttt{cost}(u) = \infty$, and $\texttt{prev}(u)=\texttt{nil}$
Pick any initial node $u_0$ and set $\texttt{cost}(u_0) = 0$ // 당연하게도 어떤 노드를 시작으로 삼든 전혀 상관이 없다!
$H=\texttt{makequeue}(V)$ // priority queue, using (cost, value) pair
// greedy process!
while $H$ is not empty
$v=\texttt{deletemin}(H)$
for each $\{v, z\} \in E$
if $\texttt{cost}(z) > w(v, z)$
$\texttt{cost}(z) = w(v, z)$, and $\texttt{prev}(z) = v$
$\texttt{decreasekey}(H, z)$
크루스컬 알고리즘과 달리 정렬이 없기 때문에, 프림 알고리즘의 시간복잡도는 Priority Queue를 쓰는데 걸리는 $E \times O(\log V) = O(E \log V)$이다.
프림 알고리즘의 형태를 잘 살펴보면, 앞에서 봤던 Dijkstra’s Algorithm과 상당히 비슷하다! 둘의 차이점은 $\texttt{cost}(\cdot)$ 업데이트 rule에서 있는데,
다익스트라 알고리즘에선 출발 노드 $s$에서 도달하는데 드는 최소 비용을 $\texttt{cost}(\cdot)$에 기록하고, 프림 알고리즘에서는 노드 $v$를 MST에 포함시킬 때의 비용을 $\texttt{cost}(\cdot)$에 기록한다.
크루스컬과 프림을 비교한다면, 개인적으론 프림이 더 쉬운 알고리즘이라고 생각한다. 왜냐하면, 프림에서는 cycle을 판단할 필요도 없고, 정말 greedy에 충실하게 노드를 선택해나가면 되기 때문이다!
이어지는 포스트에서는 <Kruskal’s Algorithm>에서 언급되었던 <Disjoint Set>에 대해 살펴본다. 이 부분은 Greedy Algorithm과 직접적으로 연관된 부분은 아니며, <Disjoint Set>이라는 자료구조를 어떻게 구현할 수 있고, 그리고 그때에 사용되는 테크닉에 대해 다룬다.
