Simplex Method
2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :) 전체 포스트는 Algorithm 포스트에서 확인하실 수 있습니다.
Simplex Method w/ Geometry
이번 포스트에서는 LP 문제를 푸는 방법인 <Simplex Method>에 대해 다룬다! 👏
먼저 이전 포스트에서 다룬 Profit Maximization 문제를 다시 살펴보자. 문제가 정의하는 inequality들로부터 feasible region을 정의한 후 직선인 objective function과 만나는 지점에서 optimum solution을 구했었다.
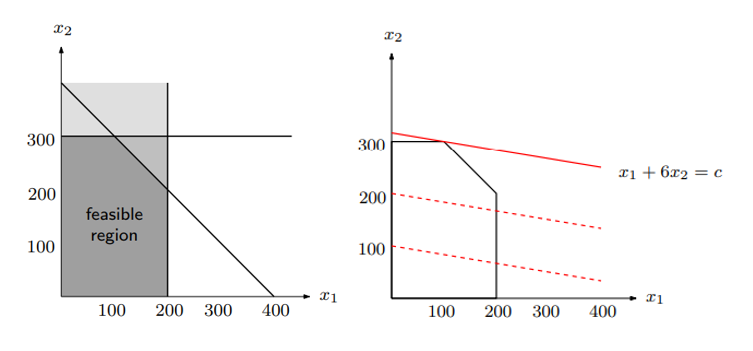
<Simplex Method>는 inequaility constraints가 만드는 feasible region의 모서리(vertex)를 순회하며 최적해를 찾는 접근이다. 위의 문제를 예로 들자면, 모서리 $(0, 0)$에서 시작해 인접한 모서리로 이동하며 더 좋은 objective value를 찾는다. 이런 모서리를 이동하는 것을 <Simplex Method>에서는 hill-climbing이라고 한다.
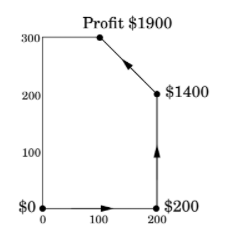
이 hill-climbing 과정은 모서리를 이동할 때마다 object value가 커지도록 한다. <Simplex Method>는 이 object value가 커지다가 감소하는 그 지점이 optimal value라고 말한다. 방법 자체는 정말 쉽지 않은가? 👏
정말 <Simplex Method>가 global optimum을 얻을 수 있는지는 간단한 기하학(Geometry)를 통해 증명한다. 만약 optimum point라고 여겨지는 정점 앞 뒤로 인접한 정점에서는 objective value가 감소한다면, 그것은 feasible region이 optimum point라고 여겨지는 정점을 지나는 직선에 완전히 덮힌다는 걸 말한다. (첫번째 그림의 오른쪽을 보라! 👀) 이것으로 증명은 충분하다.
위의 것을 좀더 보충하겠다. 일단 Linear Programming의 constraints가 유도하는 feasible region이 convex임을 보여야 한다. 그렇다면 optimum point를 지나는 직선이 feasible region을 완전히 덮는다는 걸 보장할 수 있다. 👏 feasible region의 convexity에 대해선 이곳을 참고하자.
위의 문제의 경우 variable이 $x_1$, $x_2$ 2개 이기 때문에 feasible region이 2차원에서 그려졌다. 만약 variable이 3개라면 어떻게 될까? 이때도 똑같이 feasible polyhedron을 그려서 hill-climbing을 하면 된다 👏
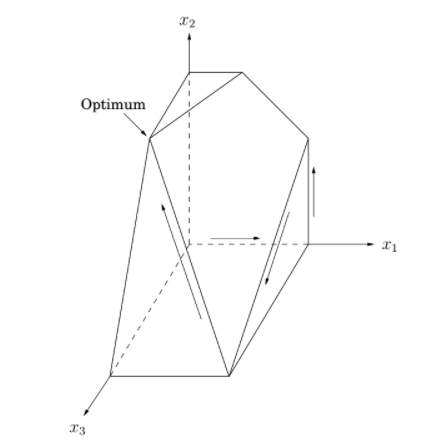
그러나 LP에서 다루는 variable이 4개를 넘어가면 더이상 도형을 그려서 hill-climbing 하는 방식으로는 최적해를 설명하거나 정당화하는 것이 불가능하다. 즉, Geometry의 한계라는 말이다.
The Simplex Method
앞 문단의 설명은 graphical 관점에서의 Simplex Method 였다. 낮은 차원에서는 직관적인 설명을 제공하지만, 다차원에서의 한계가 있었다. 이제 graphical의 관점에서 벗어나 George Dantzig가 1945년에 제시한 <Simplex Method>를 살펴보자. George Dantzig의 <Simple Method>는 컴퓨터로 쉽게 계산할 수 있는 일반적인 형태의 LP에 대한 해답을 제시한다.
일단은 간단한 예제부터 살펴보자.
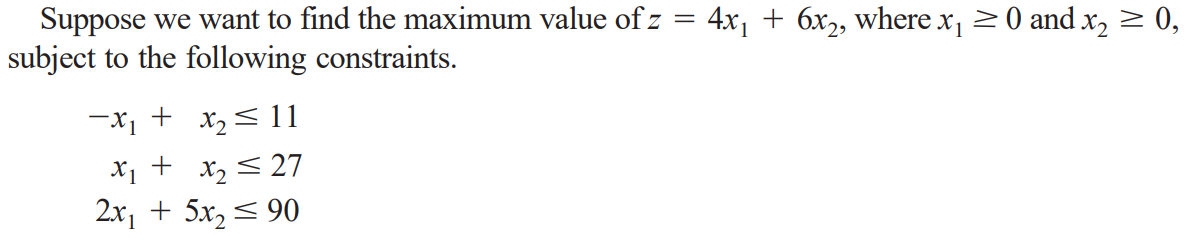
이 문제를 simplex method로 풀기 위해 inequality constraint를 equality constraint로 바꾸는 작업을 해야 한다. 이것을 standardization이라고 하며 inequality 식에 $s_i \ge 0$인 slack variable을 사용하면 된다.
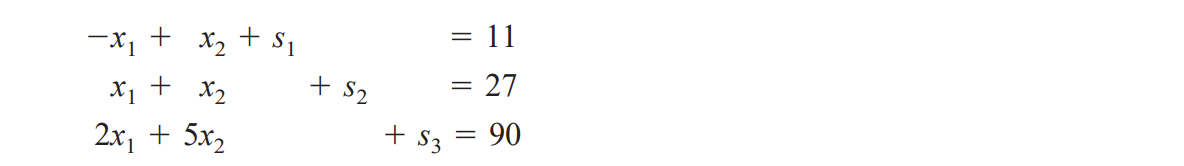
inequality constraint 하나하나 마다 slack variable $s_i \ge 0$을 추가해준다. 이렇게 하면 $s_i \ge 0$이기 때문에 원본 수식의 값은 늘 약간 모자라거나 알맞은 값을 갖게 될 것이다. slack variable로 equality constraint로 바꿔주면 기존 문제를 system of linear equations의 관점으로 바라볼 수 있게 된다.
다음은 위의 linear system을 행렬꼴로 기술한다. 이 행렬을 simplex tableau라고 한다.

위의 simplex tablaeu에서 세 가지 주목할 점이 있다.
행렬을 보면 simplex tableau 맨 마지막에 objective function에 대한 줄이 추가되었다. 맨 마지막 줄의 $b=0$이 초기 상태 $z$ 값에 대응한다. 우리는 pivoting이라는 작업을 수행해서 마지막 줄의 $b$의 값이 최대가 되도록 만들 것이다 👏
두번째는 오른편에 생긴 basic variable이라는 것이다. basic variable은 non-zero 값을 갖는 변수들을 말한다. $s_1$, $s_2$, $s_3$가 basic variable로 설정된 이유는 initial tableau의 solution이 $(x_1, x_2, s_1, s_2, s_3) = (0, 0, 11, 27, 90)$이기 때문이다.
마지막으로 simplex tableau의 마지막 줄을 통해서 optimality check를 할 수 있다. 만약 entry의 값 중 하나라도 negative value가 있다면, 그때의 solution은 optimal solution이 아니다!
Pivoting
simplex tableau에서의 solution은 $(x_1, x_2, s_1, s_2, s_3)$의 꼴로 존재한다. Pivoting은 이런 튜플 형태의 solution을 찾는 것을 목표로 한다. initial tableau에서의 solution은 $(0, 0, 11, 27, 90)$이다.
Pivoting 작업에는 몇 가지 규칙이 있어 그 규칙에 따라 순서대로 simplex solution을 찾아가야 한다. 마치 graphical approach에서 모서리를 방문하는 것과 비슷하다고 보면 된다.
current solution을 개선하기 위해선 current basic variable set에 새로운 variable을 추가해야 한다. 이 녀석을 entering variable이라고 한다. basic variable은 slack variable의 갯수를 넘을 수 없다. 그래서 기존 basic variable 중 하나가 퇴출 당해야 한다. 이 녀석을 departing variable라고 한다. 우리는 간단한 규칙에 따라 entering variable과 departing variable을 선택할 것이다.

첫번째 규칙은 맨 마지막 줄에서 가장 작은 값을 갖는 변수를 찾는 것이다. 이 변수를 entering variable으로 삼는다. 현재의 tableau에서는 $x_2$가 entering variable이다.
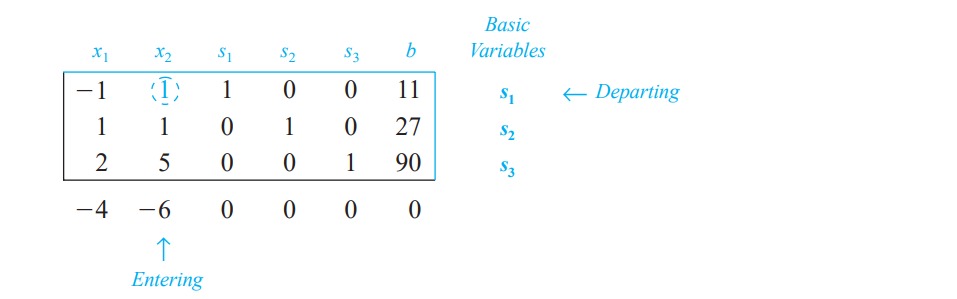
다음은 entering variable $x_2$을 값을 기준으로 ratio $b_i / a_i2$를 구한다. smallest non-negative ratio를 갖는 row의 basic variable을 선택해 departing variable으로 삼는다. 현재의 tableau에서는 $11/1=11$, $27/1=27$, $90/5= 18$로 $s_1$이 departing variable이 된다.
entering variable과 departing variable이 정해졌다면 pivot entry가 결정된다. 위의 tableau에서는 $x_2$와 $s_1$이 entering/departing variable이었고, 1st row, 2nd col의 $1$이 pivot entry가 된다. pivot entry가 결정되면, 그 entry의 값만 남도록 해당 컬럼에 대해 Gaussian Elimination을 수행한다.
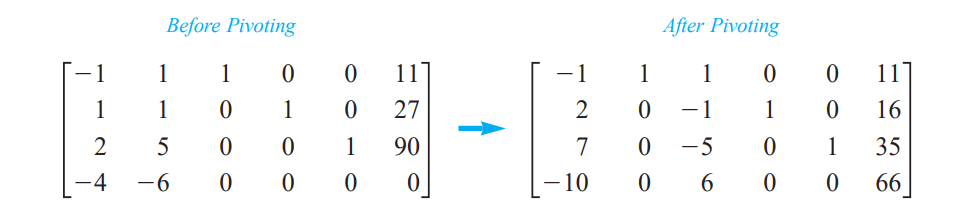

현 상태에서의 solution은 $(x_1, x_2, s_1, s_2, s_3) = (0, 11, 0, 16, 35)$가 되며, object function의 값은 $z = 4x_1 + 6x_2 = 4(0) + 6(11) = 66$이 된다. 그러나 optimality check를 해보면, 마지막 행에 $-10$이라는 음수값이 있기 때문에 아직 optimal solution이 아니며 위에서 수행한 pivoting 과정을 다시 수행해야 한다! 다시 반복하는 부분은 생-략 하겠다 🙏
Simplex Method
- (standardization) convert inequality to equality by adding slack variable $s_i$
- (standardization) convert object function in maximum form
- create the initial simplex tableau
- create bottom row by using object function
- (Pivoting) pick an entering variable by most negative entry in bottom row
- (Pivoting) pick an departing variable by most smallest non-negative $b_i / a_ij$ ratio
- (Pivoting) determine pivot entry and do Gaussian Elimination
- Do optimality check; If there exist negative entry in bottom row, then repating Pivoting!
맺음말
이것으로 Linear Programming의 기법들을 모두 살펴보았다!
References
- Larson: Elementary Linear Algebra, 4 ed., Ch.9.3: The Simplex Method: Maximization
