Density Estimation
2021-1학기, 대학에서 ‘데이터 마이닝’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :)
Density Estimation이란?
이번에 살펴볼 <Density Estimation>은 주어진 데이터로부터 probaiblity density function, pdf를 복원하는 작업이다. 확률론에 익숙하다면, <Point Estimation>, <Internal Estimation> 등의 추청(Estimation) 기법을 들어봤을 것이다. <Density Estimation>은 pdf를 추정하는 작업으로 다른 Estimation 처럼 Confidence Interval도 구할 수 있다고 한다.
<Density Estimation>(이하 DE)은 왜 필요할까? DE의 목적인 pdf를 얻기 위해서이다. pdf를 안다면 우리가 가진 데이터가 어떤 성질을 가졌는지 추측하기 쉬워진다. 예를 들어 정규 분포와 같은 bell shape인지, 반대로 양극단에 몰려있는지, 아니면 초반에 몰려있는 skewed 형태인지를 안다면 어떤 모델을 쓰고, 어떻게 데이터 정규화를 할 것인지 결정하는데 도움이 된다.
DE는 분류상 Unsupservised Learning로 분류된다. DE는 non-parameteric DE, parameteric DE로 더 나뉘어지는데, 이번 포스트에선 non-parameteric DE만 살펴본다.
Discrete Case: Histogram
먼저 density estimation의 이산적인 방법을 살펴보자! 사실 개념 자체는 간단한데, 데이터 범위를 몇개의 영역(bin)으로 쪼개서 해당 영역에 존재하는 데이터의 수를 세어주기만 하면 된다. 일종의 히스토그램(histogram)을 만드는 것이다!
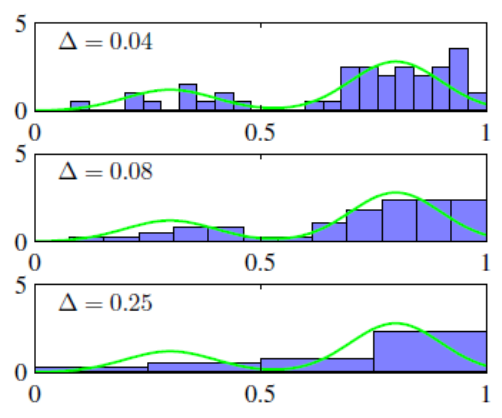
수식도 직관적이다.
we observe $X_1, …, X_n$, and $\Delta_i$ is bin width.
\[p_i = \frac{n_i}{N \times \Delta_i} = \frac{\text{# of observations}}{\text{# of samples} \times \text{bin width}}\]Histogram은 non-parametric DE에 속한다. 정확히 말하자면, probability mass function을 구한 것이긴 한데… 아무튼 DE 중 하나로서 소개된다. 데이터가 Discrete한 경우에 적합한 접근이다.
위의 사진을 보면, $\Delta$ 값이 커질 수록 global trend를 반영하고, 값이 작을 수록 local trend를 반영하는 걸 볼 수 있다.
Kernel Density Estimation
Histogram이 이산적인 경우라면, KDE는 연속적인 데이터에 적합한 DE 방식이다. Histogram에선 $p_i$를 구했다면, KDE에선 $p(x) (x \in \mathbb{R})$를 구한다.
그러나 현실에서 우리가 찾고자 하는 $x \in \mathbb{R}$에 정확하 어떤 데이터가 존재하는 일은 거의 없다. 그래서 $x$의 주변 데이터를 이용해 $p(x)$를 추정해야 한다. 어느 정도의 데이터를 “주변(neighborhood)”로 여길 것인지를 결정하는 함수가 바로 kernel function $k(u)$이다.
kernel function: parzen window
\[k(u) = \begin{cases} 1 & \left| u \right| \le 1/2 \\ 0 & \text{otherwise} \end{cases}\]where $u$ is distance between $x$ and other data point.
위의 커널 함수는 가장 간단한 형태로 주변 $1/2$ 거리의 점들을 “neighborhood”로 여기겠다는 말이다. 그래서 $x$ 주변에 몇개의 데이터가 있는지를 계산해보면,
\[K(x) = \sum^N_{i=1} k(x - x_i)\]그런데, neighbor를 주변 $1/2$ 범위로 고정하는 건 별로 유연하지 않다. 그래서 유연성을 위해 size $h$를 도입한다.
\[K(x; h) = \sum^N_{i=1} k \left(\frac{x - x_i}{h} \right)\]size $h$는 Histogram에서의 bin $\Delta_i$와 같은 역할이다. 좌우 $1/2 \Delta_i$ 만큼을 neighbor로 삼는다는게 어떻게 위와 같은 형태가 되는지 아래의 과정을 따라가보자.
\[\begin{aligned} \left| u \right| &\le 1 / 2 \Delta_i \\ \left| u / \Delta_i \right| &\le 1 / 2 \\ \left| (x - x_i) / \Delta_i \right| &\le 1 / 2 \\ \end{aligned}\]그래서 neighbor 범위를 더 넓게/좁게 잡고 싶다면, $h$의 값을 조정하면 된다.
아직 $x$의 size $h$에 있는 neighbor의 숫자 $K(x; h)$만 구했다. 확률 $p(x)$는 기존 histogram의 확률 $p_i$와 비슷하게 유도하면 된다.
\[\begin{aligned} p_i &= \frac{n_i}{N \Delta_i} \\ p(x) &= \frac{K(x; h)}{N h} \end{aligned}\]어떤가? KDE 너무 쉽지 않은가? :)
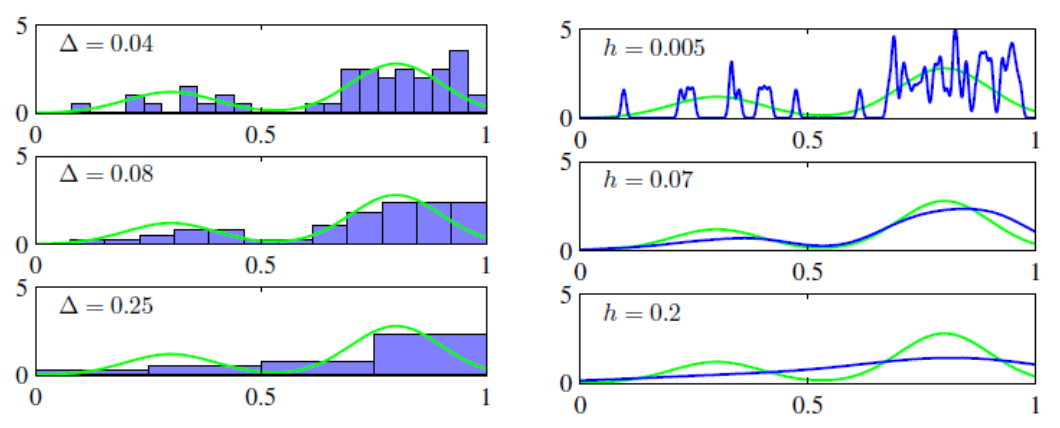
Histogram과 KDE를 통해 구한 pmf, pdf를 비교한 그림이다. 마찬가지로 $h$ 값이 커질 수록 global trend, 작을수록 local trend를 반영한다. KDE에선 범위가 더 적은 범위를 쓰기에 $h=0.005$에서 0인 값이 꽤 된다.
$\Delta$, $h$는 hyper parameter이기 때문에 어떤 값을 써야 하는지는 Domain Knowledge의 개입이 필요하다.
2차원 이상에서 KDE
분포를 추정하는 데이터가 1차원이 아닌 2차원 이상의 $d$-dimensional data인 경우도 있을 것이다. 그럴 때는 $h^d$의 cube 범위 내의 neighbor를 구하면 된다.
맺음말
예전에 컴퓨터 비전 수업을 들을 때, <Sequential Density Estimation>이란 걸 배웠었다. 그때는 확률론을 전혀 모르고, <Density Estimation>도 전혀 모르는 상태에서 들어서 그 의미를 모르고 무작정 수식을 외웠던 기억이 있다. 나중에 해당 내용을 다시 살펴봐야 할 것 같다.

