Satisfiability(SAT)
2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :)
Satisfiability 문제, 줄여서 SAT 문제는 주어진 Boolean formula를 만족시킬 수 있는 true/false 값을 Boolean 변수들에 적절히 할당하는 문제다. 구체적으로 Boolean formula는 CNF(conjunctive normal form) 형태로 주어진다.
\[(x \lor y \lor z) (x \lor \bar{y}) (y \lor \bar{z}) (z \lor \bar{x}) (\bar{x} \lor \bar{y} \lor \bar{z})\]“Given a Boolean formula in CNF, either find a satisfying truth assignment or report ‘none exists’.”
단순하게 완전 탐색으로 접근하면, $n$개의 boolean variable에 대해 $2^n$개의 가능한 모든 assignment를 순회하며 주어진 Boolean formula에 할당해 문제를 해결하면 된다. 그래서 SAT 문제는 이진 트리를 탐색하는 전형적인 search problem에 속한다.
Variation of SAT
아무 제약조건이 없는 순수한 SAT 문제를 푸는 것은 NP지만, 아래의 변형에 대해선 효과적인 알고리즘이 제시되었다!
Horn formula
“All clauses contain at most one positive literal. Find a satisfying truth assignment.”
Greedy Algorithm을 통해 linear-time에 해를 찾을 수 있다.
2 SAT
“All clauses have only two literals. Find a satisfying truth assignment.”
Strongly Connected Components 문제로 환원(reduction)해 linear-time에 해를 찾을 수 있다.
위 문제들에 대한 내용은 별도의 포스트에서 탐구해보도록 하고 지금은 SAT 문제가 무엇인지만 확인하고 넘어가자.
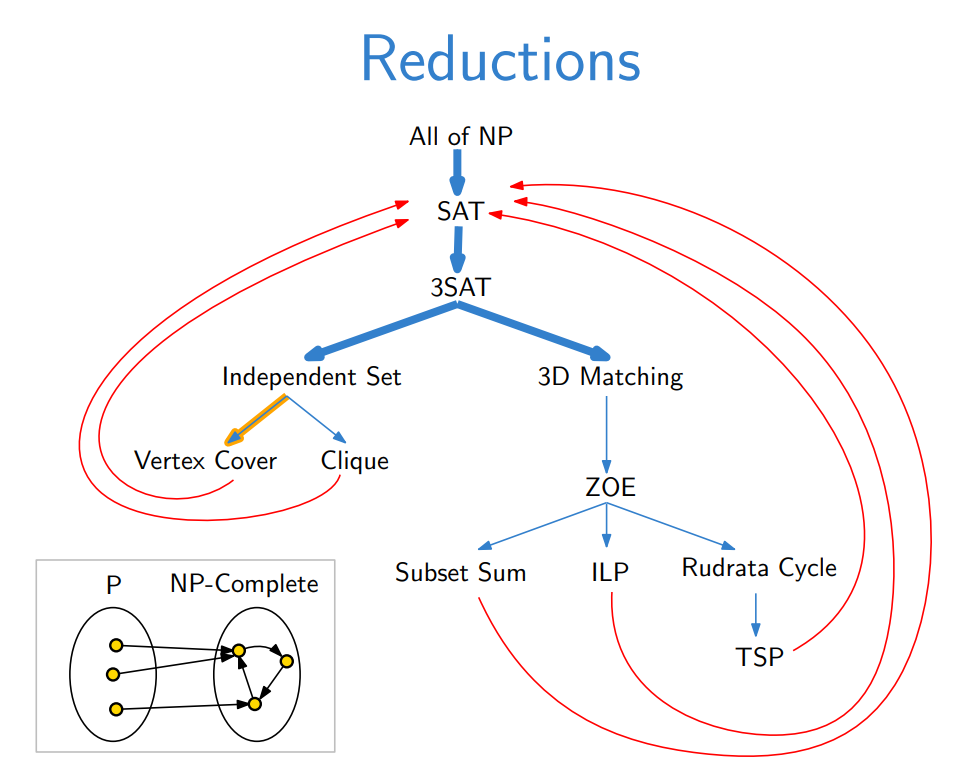
SAT 문제는 NP 문제 중에서 기본이 되는 문제다. 그래서 거의 모든 NP 문제들이 SAT 문제의 꼴로 환원할 수 있다. 해당 내용은 추후에 Reduction 포스트에서 더 살펴보도록 하겠다.