P and NP
2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :) 전체 포스트는 Algorithm 포스트에서 확인하실 수 있습니다.
Search Problems
지금까지 우리가 풀었던 대부분의 문제는 지수적으로 가능한 모든 케이스(exponentially possible cases)를 모두 탐색한다면 해결할 수 있었다. 이때, 우리가 찾는 해(解)는 path, tree, matching 등이 될 수 있는데
- $n$명의 소년을 $n$명의 소녀와 매칭 → $n!$
- $n$개 노드가 있는 완전 그래프의 spanning tree → $n^{n-2}$ Caley’s Formula [link]
- undirected graph에서 노드 $s$에서 노드 $t$로 가는 path의 수 → exponentially many
위와 같이 그래프나 매칭 문제를 풀기 위해 ‘가능한 모든’ 경우를 살펴본다면 exponentially many한 경우의 수를 모두 탐색해야 하고, 이것은 실전에서는 불가능하다. 그래서 지금까지는 exponentially many한 경우를 모두 살펴보는게 아니라 알고리즘 테크닉을 활용해 polynomially many한 경우만 살펴보고 문제를 해결했다!
- Minimum Spanning Tree
- Greedy Algorithm: $O(E \log V)$
- $s-t$ shortest path
- Dijkstra’s Algorithm: $O((V + E) \log V)$
- Chain Matrix Multiplication
- Dynamic Programming: $O(n^3)$
- Bipartitie Matching
- Network Flow(Linear Programming): $O(n^3)$
그러나 위의 케이스가 운이 좋은 것일 뿐, 여전히 많은 search problem들의 가장 빠른 알고리즘이 exponential complexity를 가지고 있다. 이번 챕터에서는 이런 exponential complexity 만으로 해결 가능한 문제들에 대해 살펴보겠다 👏
P and NP
- 결정 문제(Deterministic Problem)
- 답이 YES 아니면 NO로 반환되는 문제
- ex. $a$는 $b$의 배수인가?
- 다항 시간 알고리즘(polynomial time algorithm)
- 시간 복잡도가 $O(n^2), O(n^3), …, O(n^k)$인 경우를 말함.
- 지수 시간 알고리즘(exponential time algorithm)
- 시간 복잡도가 $O(2^n), O(3^n), … O(n^n)$인 경우를 말함.
여기까지는 이미 알고 있는 내용이다.
“모든 Search Problem은 proposed solution $S$가 주어졌을 때, 그것이 정말로 solution인지 아닌지 poly-time 안에 판단할 수 있다.”
“For any search problem, there is an efficient checking algorithm $C$ that takes as input the given instance $I$(amount of input data), as well as the proposed solution $S$, and outputs $true$ if and only if $S$ really is a solution the problem. Moreover the running time of $C(I, S)$ is bounded by a polynomial in $| I |$, the length of the instance.”
가젤_gazelle님의 ‘P vs NP 쉽게 이해하기’ 포스트가 결정적/비결정적 알고리즘을 이해하는데 큰 도움이 되었습니다 🙏
- 결정적 알고리즘(deterministic algorithm)
- 계산의 각 단계에서 단 한 가지 선택지만 고려하는 알고리즘
- DFS는 deterministic이다. 왜냐하면 방문하는 순서가 명확히 정해져 있기 때문이다: pre-order, post-order, in-order
- 마찬가지로 merge sort도 deterministic이다. Divide-and-Conquer로 풀지만 문제를 푸는 순서는 함수콜 순서를 생각하면 stack에 쌓인 순서대로 처리하기 때문에 순서가 명확하다.
- 비결정적 알고리즘(non-deterministic algorithm)
- 계산의 각 단계에서 여러 가지 선택지를 ‘동시에’ 고려하는 알고리즘
- 가젤님의 아티클에서는 비결정적 알고리즘이 선택지를 ‘동시에’ 고려하는 걸 “분신술”이 비유했습니다!
- 제가 공부한 전공 서적에서도 Non-deterministic Algorithm은 “A special (and quite unrealistic) sort of algorithm can find and verify the search problem in polynomial time.”으로 기술하고 있습니다. “분신술”이라는 unrealistic 방법을 쓰는 알고리즘이기 때문에 가상에서만 존재하는 알고리즘이죠.
몇가지 사례를 통해 Non-deterministic Algorithm을 살펴봅시다.
[원소 합이 0이 되는 부분집합]
$\{ -5, 6, 1, 2, -10, -7, 13 \}$라는 정수 $n$개의 집합이 있을 때, 이 집합의 부분 집합 중 원소의 합이 0이 되는 부분 집합이 존재하는지 Yes/No로 대답하라.
length $n$을 갖는 boolean sequence $(0, 0, …, 1)$로 부분집합을 표현해 모든 부분집합 조합을 모두 확인해 원소 합이 0이 되는지 확인한다.
이 문제를 Deterministic Algorithm으로 푸려고 한다면, $O(2^n)$ 만큼의 시간이 걸린다. 그러나 마법의 Non-deterministic Algorithm으로 푼다면 $O(n)$의 시간으로 풀 수 있다. 뒤에서 나오겠지만, Non-deterministic polynomial solvable 이므로 Class $\textbf{NP}$에 속한다!
[외판원 문제: 모든 정점을 단 한번씩 방문하는 길이 존재하는가?]
이 문제도 polynomial time 알고리즘이 존재하지 않는다. 그러나 $n$개 노드의 permutation을 동시에 살펴볼 수 있는 마법의 Non-deterministic Algorithm으로 푼다면 $O(n)$의 시간으로 풀 수 있다. 바로 위의 [원소 합이 0이 되는 부분집합] 문제와 비슷하지만 조금 다른 Non-deterministic Algorithm이다.
맨 첫 방문이 1인 permutation을 생각해보자. 다음 방문은 $2 \sim n$이 가능할 것이다. 분신술을 써서 $(n-1)$ 갈림길을 동시에 모두 확인한다. 각각의 갈림길에서 $(n-2)$ 갈림길을 또 동시에 모두 확인한다…
이렇게 동시에 방문할 수 있다면, non-deterministic algorithm으로 $O(n)$ 시간에 해결 가능하므로 Class $\textbf{NP}$에 속한다!
- Class P는 Deterministic Algorithm으로 poly-time 안에 solvable한 문제다.
- ex. $a$는 $b$의 배수인가? → 유클리드 호제법으로 풀 수 있음
- 반면 Class $\textbf{NP}$는 Non-deterministic Algorithm으로 poly-time 안에 solvable한 문제
- ex. [원소 합이 0이 되는 부분집합], [외판원 문제]
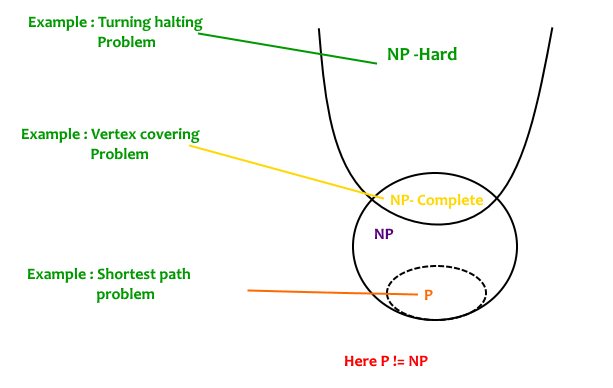
- 모든 Deterministic Algorithm은 Non-deterministic Algorithm에 포함되기 때문에 Class P는 Class $\textbf{NP}$에 포함된다.
- Class $\textbf{NP}$ 문제에 해당하더라도 적절한 Algorithm Technique을 사용하면 Class $\textbf{P}$에 속하는 문제들도 있다.
- 정렬 문제는 permutation을 모두 확인하는 Non-deterministic Algorithm으로 풀 수 있는 Class $\textbf{NP}$ 문제이지만, 적절한 Deterministic 정렬 알고리즘을 사용한다면 $O(n^2)$ 또는 $O(n \log n)$으로 해결할 수 있는 Class $\textbf{P}$ 문제이다.
계산 이론의 미해결 문제로 “Class $\textbf{P}$와 Class $\textbf{NP}$가 동일한 집합인지”를 판단하는 P=NP 문제가 있다. 가능한 결론으로는 아래 세 가지가 있다.
- $\textbf{P} = \textbf{NP}$, 즉 “모든 $\textbf{NP}$ 문제는 $\textbf{P}$문제이다.”가 참이라면 “쉽게 검산할 수 있는 모든 문제들은 모두 쉽게 풀 수 있다, 즉 쉽게 푸는 알고리즘이 존재한다.”
- $\textbf{P} \neq \textbf{NP}$, 즉 “Deterministic Algorithm으로 풀 수 없는 Class $\textbf{NP}$ 문제가 존재한다.”
- 증명할 수 없다.
$\textbf{P}$와 $\textbf{NP}$를 잘 이해했다면 다음은 $\textbf{NP-complete}$와 $\textbf{NP-hard}$를 이해하고 싶을 것이다. 그러나 Stay… 이 두 개념을 이해하려면 환원(reduction)을 먼저 이해해야 하는데, reduction을 아무 바탕없이 바로 이해하려고 하면 어렵지만 하다. 그래서 여러 $\textbf{NP}$ class 문제들을 살펴보고, 그 $\textbf{NP}$ class 문제들이 서로 어떻게 환원(reduction) 되는지를 살펴본 후에 마-지막에 $\textbf{NP-complete}$와 $\textbf{NP-hard}$의 개념을 살펴볼 것이다 👏
- Satisfiability (SAT)
- Traveling Salesman Problem (TSP)
- Hamilton Cycle Problem (HCP)
- Balanced Cut
- 3D Matching
- Integer Linear Programming
- Independent Set, Vertex Cover, Clique
- Longest Path, Subset Sum
