Reduction (3)
2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :) 전체 포스트는 Algorithm 포스트에서 확인하실 수 있습니다.
미리 밝히자면 이번 내용은 좀 어렵다! 흐름을 잘 따라가보자!
3-SAT → 3D-Matching
Claim. 3-SAT $\le_P$ 3D-Matching
아래와 같은 3-SAT 문제를 3D-Matching 문제로 환원해보자.
\[(\bar{x} \lor y \lor z)(x \lor \bar{y} \lor z)(\bar{x} \lor y \lor w)\]Gadget
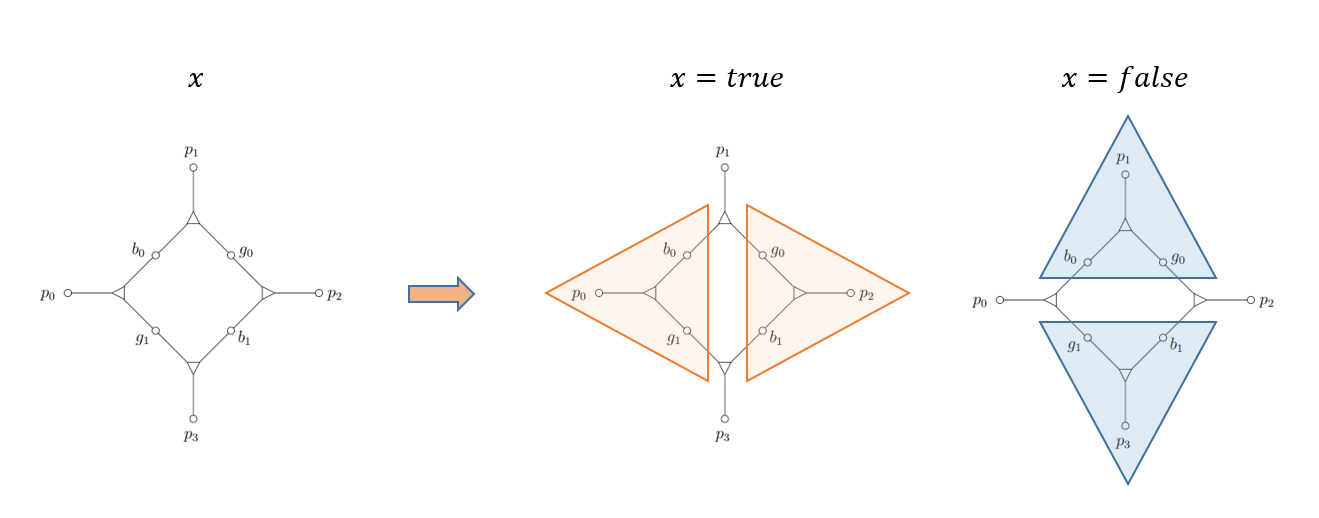
먼저 4개의 triplet이 모여 만들어진 gadget이라는 녀석을 살펴보자. 오른쪽 그림을 보면 알 수 있듯, 이 녀석은 위-아래, 또는 좌-우로밖에 3D-Matching을 할 수 밖에 없다. 녀석의 이분적인 특징을 바탕으로 gadget을 일종의 boolean variable로 취급할 것이다! 만약 $b_0$가 $g_1$와 매칭된다면, $\text{true}$로 $b_0$가 $g_0$와 매칭된다면, $\text{false}$로 취급하겠다.
Proof
Given an instance $\Phi$ of 3-SAT, we construct an instance of 3D-Matching that has a perfect matching iff $\Phi$ is satisfiable.
* “perfect matching”이란 서로 좋아하는(preference)가 있는 정점끼리 매칭된 경우를 말한다. Bipartite Matching의 Solution은 perfect matching이다.
[Problem Transformation]
1. 3-SAT에 존재하는 모든 변수 $x_i$를 gadget으로 만든다.
2. 3-SAT에 존재하는 Clause $C_j$를 표현하는 clause gadget을 만든다.
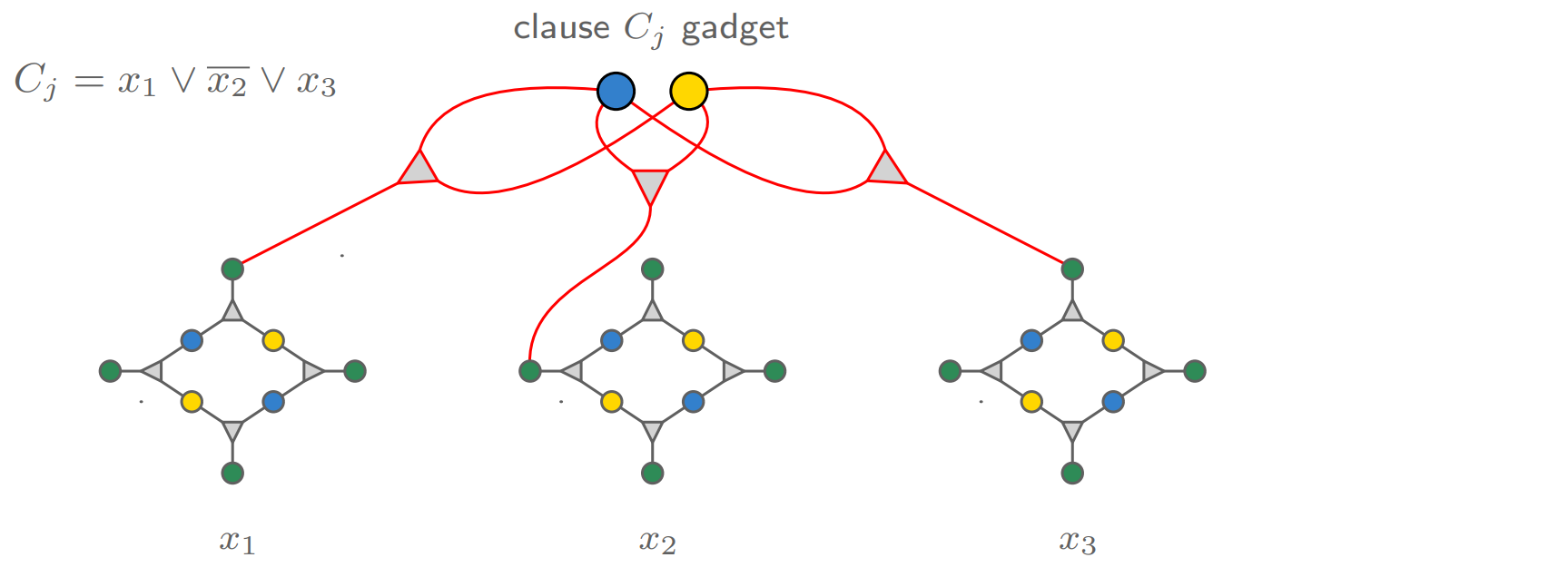
clause gadget을 만들기 위해 새로운 boy $b_c$, girl $g_c$를 도입한다. 이 $b_c$, $g_c$와 각 variable gadget의 pet 중 하나와 연결해 새로운 triplet들을 만들 것이다. clause $C_j$가 satisfying 하려면, 3가지 $(b_c, g_c, p)$ triplet 중 적어도 하다가 매칭 되어야 한다. 그런데 $b_c$, $g_c$에 연결할 pet $p$는 어떻게 결정해야 할까?
$C_1 = (x \lor \bar{y} \lor z)$라는 clause를 만족하려면, (1) $x = \text{true}$ (2) $y = \text{false}$ (3) $z = \text{true}$, 셋 중 하나여야 한다. 만약 (1) $x = \text{true}$을 만족해서 clause $C_1$이 만족된다고 하자. 그럼 gadget $x$는 좌우 매칭, $(b_{x0}, g_{x1}, p_{x0})$, $(b_{x1}, g_{x0}, p_{x2})$인 상태일 것이다. 이 경우라면, $b_c, g_c$가 매칭이 생기기 위해선 $x$의 gadget과 연결된 triplet이 매칭 되어야 한다. 그래서 아직 매칭이 되지 않은 $p_{x1}, p_{x3}$ 중 하나를 선택해 $(b_c, g_c, p)$ triplet을 생성한다.
그러나 $x$에 $\text{false}$가 할당될 수도 있기에 $x = \text{false}$인 상황을 생각해보자. 그러면, $p_{x1}, p_{x3}$가 이미 취해졌기 때문에 $C_1$의 clause gadget에서 $x$ gadget의 pet과 연결된 triplet은 매칭될 수 없다.
3-SAT → Constrained 3-SAT
그러나 위와 같이 Clause Gadget으로 3-SAT 문제를 3D-Matching으로 바꾸게 되면, 문제가 발생한다! 예를 들어, boolean variable $x$가 3-SAT에서 3개 이상의 Clause에서 등장한다면, 3D-Matching 인스턴스를 만들 수 없다!! 예를 들어 아래 3-SAT을 3D-Matching 문제로 변환해보자.
\[\Phi = (x \lor y \lor z)(x \lor \bar{y} \lor z)(x \lor y \lor \bar{z})\]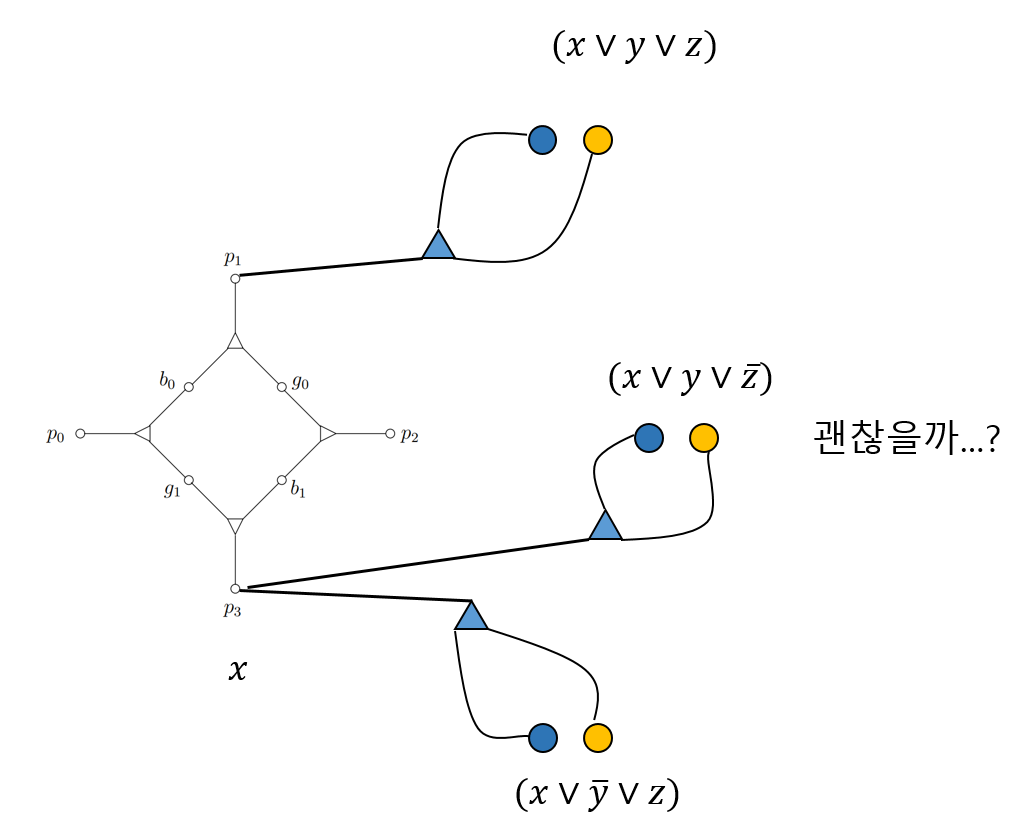
마지막 clause $(x \lor y \lor \bar{z})$를 $p_3$에 붙여 triplet을 만들었다고 하자. 그런데 만약 $(x \lor \bar{y} \lor z)$도 $(x \lor y \lor \bar{z})$도 $x=\text{true}$라서 $x$와 연결된 triplet이 매칭 되어야 한다고 해보자. 그럼 $p_3$에 붙은 triplet 2개 모두 매칭이 되어야 하는데, 이것은 pet $p_3$가 중복해서 매칭되기 때문에 더이상 perfect matching이 아니다!
정확하게 말하자면, variable이 3개 이상의 Clause에 등장하는 것이 아닌 literal이 3개 이상의 Clause에 등장하지 않아야 한다. 이때, literal이란 negation을 구분하는 것으로 $x$와 $\bar{x}$를 서로 다른 literal이라고 한다.
위와 같이 literal이 3개 이상 등장하는 문제를 해결하기 위해, 3-SAT 문제를 <Constrained 3-SAT> 문제로 Reduction 해야 한다. <Constrained 3-SAT> 문제란 “각 literal이 최대 2번 등장하는 3-SAT 문제”이다.
Proof
Let $\Phi$ be an instance of 3-SAT. For each literal $x$ appearing in $\Phi$ more than three times, replace each appearance of $x$ by a new literal, say $x_1, x_2, …, x_k$. Then add the clause
\[(\bar{x_1} \lor x_2)(\bar{x_2} \lor x_3) \cdots (\bar{x_k} \lor x_1)\]$k$ is the number of appearance of $x$ in $\Phi$. Then, replace each appearance of $x$ into $x_i$.
Then, the transformed 3-SAT problem is Constrained 3-SAT!
위의 변환 과정에서 도입한 $(\bar{x_1} \lor x_2)(\bar{x_2} \lor x_3) \cdots (\bar{x_k} \lor x_1)$ clause 절은 각 literal $x_i$가 모두 같은 값을 가지도록 만든다: $x_1 = x_2 = \cdots = x_k$. 어떤 variable $x_i$ 하나의 값을 정했을 때, 위의 clause 절이 어떻게 만족되는지를 살펴보면 이 사실을 금방 확인할 수 있다.
Constrained 3-SAT → 3D-Matching
다시 본래의 문제로 돌아와보자. 자, 이제 하나의 literal이 최대 2번 등장하기 때문에 앞에서 살펴본 perfect matching이 안 되는 그런 문제를 걱정하지 않아도 된다! 그런데, 아직 하나의 작업이 남았다.
만약 3-SAT 문제에 $n$개의 variable, 그리고 $m$개의 clause가 있다면, 해당 3-SAT 문제가 satisfying 된 후, 즉 적절한 3D-Matching을 찾은 후에는 $2n - m$개의 매칭되지 않은 남은 pet들이 있다. 이들을 위해서 triplet을 만들어줘야 perfact 3D-Matching이 가능하다고 한다. 이를 위해 “generic animal-lover”인 boy-girl 커플을 만들어 pet들을 모두 연결해준다. (generic animal-lover이기에 triplet이 없는 pet, 있는 pet 모두 연결된 커플이다.)
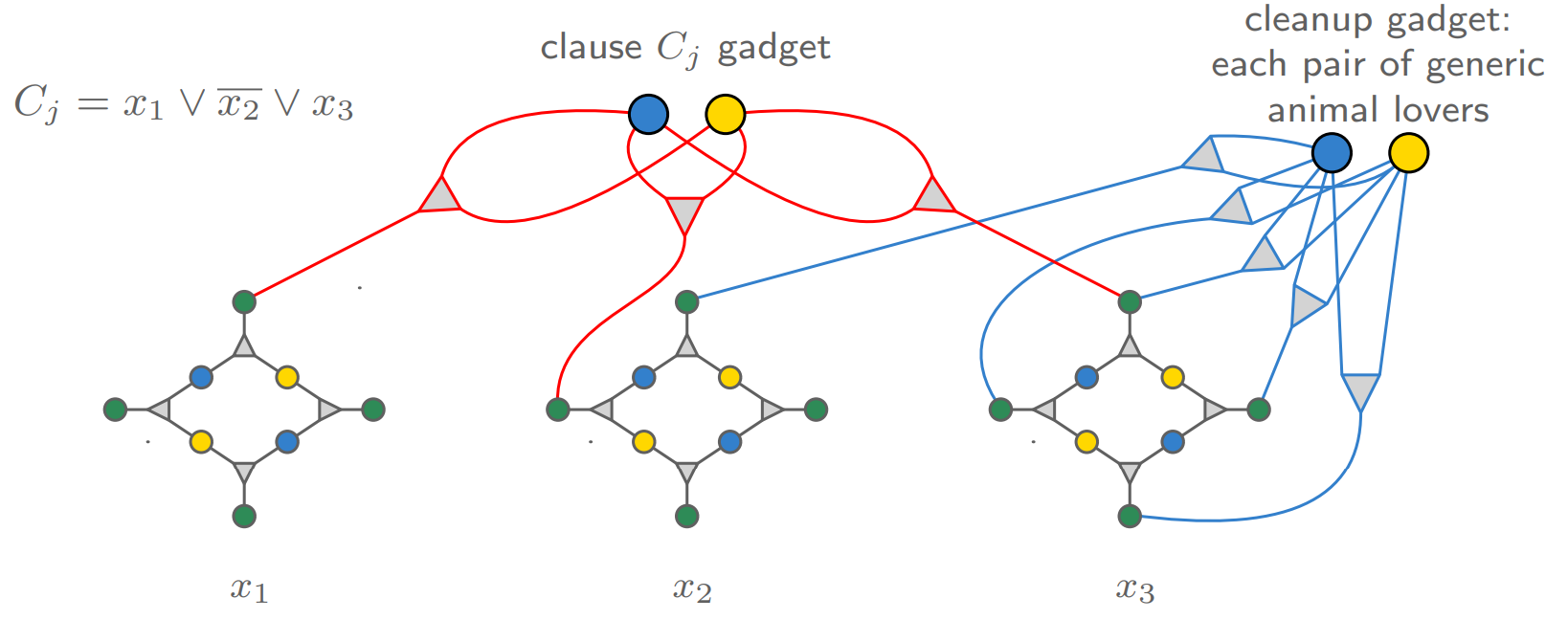
전체 3-SAT 문제에 대해서 보면 아래와 같다.
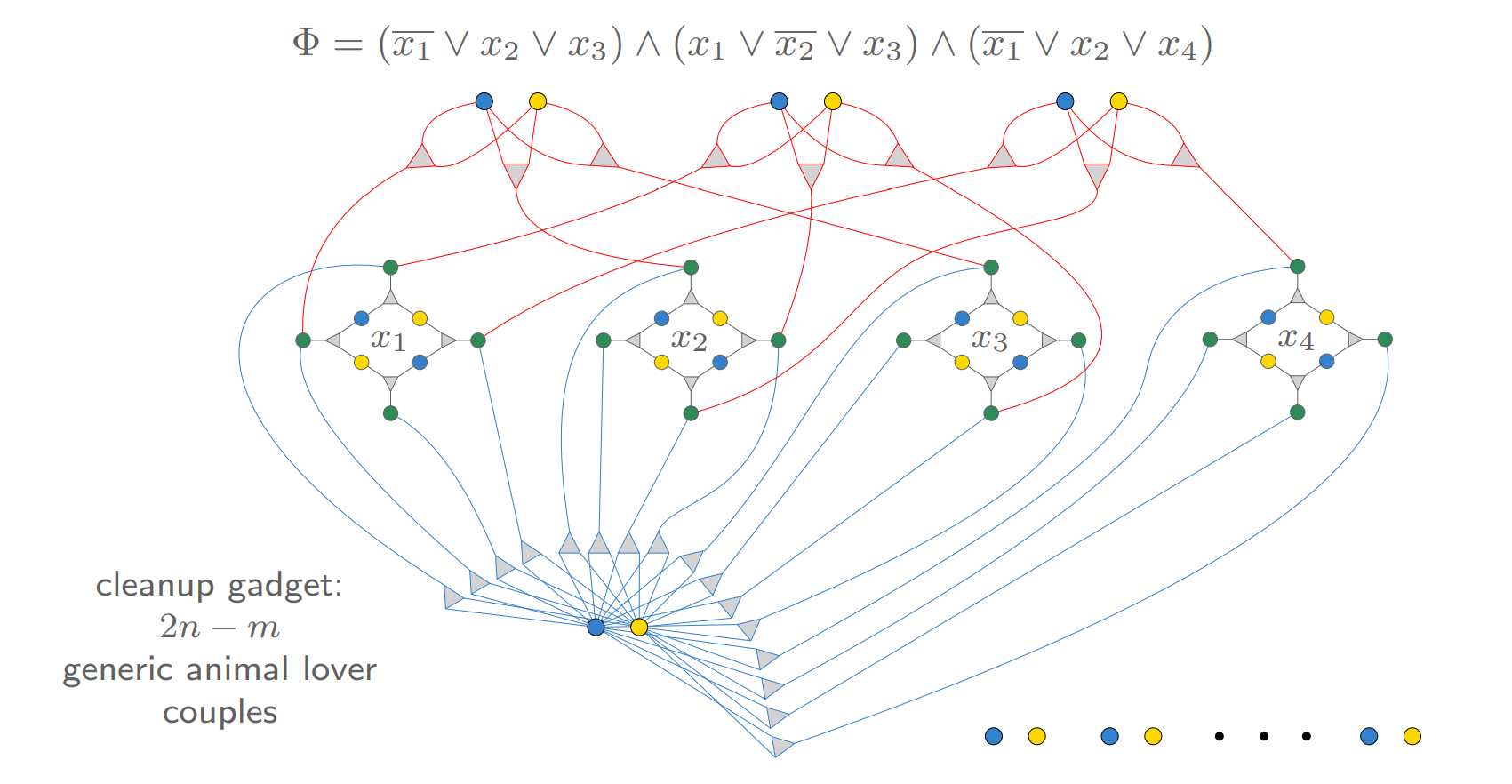
보면, 위 그림에는 하나의 generic animal-lover couple만 표현되어 있다. 그러나 그림의 오른쪽 아래를 보면, boy-girl couple이 더 존재하는데, 이들 모두 generic animal-lover다! 이런 couple이 $2n-m$개 존재한다고 보면 된다. 이들은 매칭되지 않은 pet들을 매칭하기 위한 존재들이다.
