Reduction and NP-complete
2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :) 전체 포스트는 Algorithm 포스트에서 확인하실 수 있습니다.
(Review) P and NP
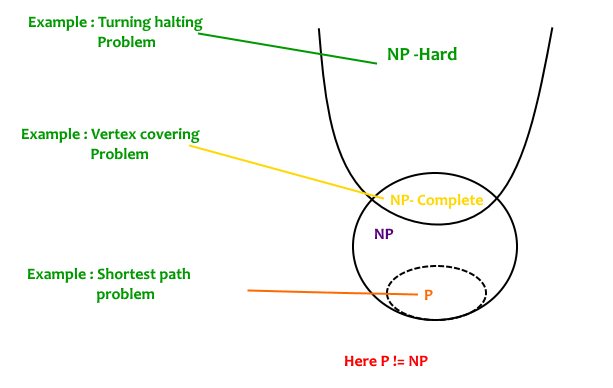
잠깐 이전 내용을 복습해보자.
- $\textbf{NP}$: the class of all search problems
- $\textbf{P}$: the class of all search problems that can be solved in polynomial time.
그리고 $\textbf{P} = \textbf{NP}$ 인지 $\textbf{P} \neq \textbf{NP}$ 인지에 대한 논쟁도 잠깐 다뤘다. 대부분의 연구자들은 $\textbf{P} \neq \textbf{NP}$라고 믿고 있다. 그러나 $\textbf{P} \neq \textbf{NP}$임을 밝히는 명확한 증명이 있는 건 아니다. 그들은 왜 $\textbf{P} \neq \textbf{NP}$라고 믿는 걸까?
그들은 ‘증거’를 가지고 있기 때문이다! $\textbf{NP}$에 속하는 몇몇 search problem은 몇십년, 몇백년이 걸려도 효율적인 알고리즘을 찾을 수 없었다는 경험적인 증거가 있다. 또, 하나의 증거는 환원(Reduction)으로, 그런 hardest problem들이 equivalent under reduction라는 것이 증명 되었기 때문이다!
What reductions demonstrate is that the problems are all, in some sense, exactly the same problem, except that they are stated in different languages.
이번 챕터에서는 $\textbf{NP}$의 hardest problem들이 어떻게 equivalent under reduction 한지 가볍게 살펴보겠다.
Reduction

Definition. Reduction (search problem)
A reduction from search problem $A$ to search problem $B$ is a polynomial-time algorithm $f$ that transforms any instance $I$ of $A$ into an instance $f(I)$ of $B$.
Together with another polynomial-time algorithm $h$ that maps any solution $S$ of $f(I)$ back into a solution $S$ of $f(I)$ back into a solution $h(S)$ of $I$.
즉, <Reduction>이라 함은
- instance $I$를 변환(transform) 하는 polynomial-time algorithm $f$
- $f(I)$의 solution $S$를 $I$의 solution으로 변환하는 polynomial-time algorithm $h$
즉 $f$와 $h$, 2가지 알고리즘이 필요한 작업이다!
그런데 <Reduction>을 하는 이유가 뭘까? 거기엔 2가지 목적이 있다.
- We know how to solve $B$ efficiently, and want to utilize it to solve $A$
- We know $A$ is hard, and use the reuction to prove $B$ is hard as well.
보통의 경우들에는 목적 1을 이루기 위해 <Reduction> 작업을 수행한다. 그러나 이번 경우에는 Problem B가 Problem A만큼 ‘어렵다‘는 증명하는 목적 2를 위해서 <Reduction> 작업을 수행한다!!
본인은 처음에 위의 문장들이 잘 이해가 안 되었다. Reduction으로 유도되는 Problem B의 Difficulty가 부자연스러워 보였기 때문이다. 본인은 Reduction은 문제를 해결하기 위한 수단, 즉 목적 1에 대해서만 온전히 이해하고 있었다.
그러나 Wikipedia에 기술된 아래 구절을 읽고 목적 2를 온전히 이해할 수 있었다.
Intuitively, problem A is reducible to problem B if an algorithm for solving B efficiently could also be used as a subroutine to solve problem A efficiently. When this is true, solving A cannot be harder than solving B. “Harder” means having a higher estimate of the required computational resources in a given context.
즉, problem A에서 problem B가 Reduction이 가능한 순간부터 Difficulty에 대한 bound가 생기는 셈이다. 그것은 ‘solving A cannot be harder than solving B’라는 문장으로 표현된다. 이것은 Difficulty of B가 Difficulty of A의 upper bound가 된다는 셈이며, 바꿔말하면 Difficulty of A가 B의 lower bound가 된다는 셈이다.
\[A \rightarrow B \implies \text{Dfficulty of A} \le \text{Difficulty of B}\]Reduction를 수식으로 표현면 $A \rightarrow B$ 또는 $A \le_p B$로 표현할 수 있다. “$B$ is polynomial-time reducible to $A$”라고 읽으면 된다. $A \le_m B$도 있는데, subscript가 $p$인지 $m$인지에 따라 mapping reduction, polynomial reduction으로 나뉜다. 이에 대해서는 별도의 포스트에서 다루도록 하겠다.
NP-complete
이제 <Reduction>이 무엇인지 대충 알았으니 $\textbf{NP-complete}$의 개념을 정의해보겠다.
Definition. $\textbf{NP-complete}$
A search problem is $\textbf{NP-complete}$ if all other search problems reduce to it.
텍스트와 함께 아래 그림을 살펴보자.
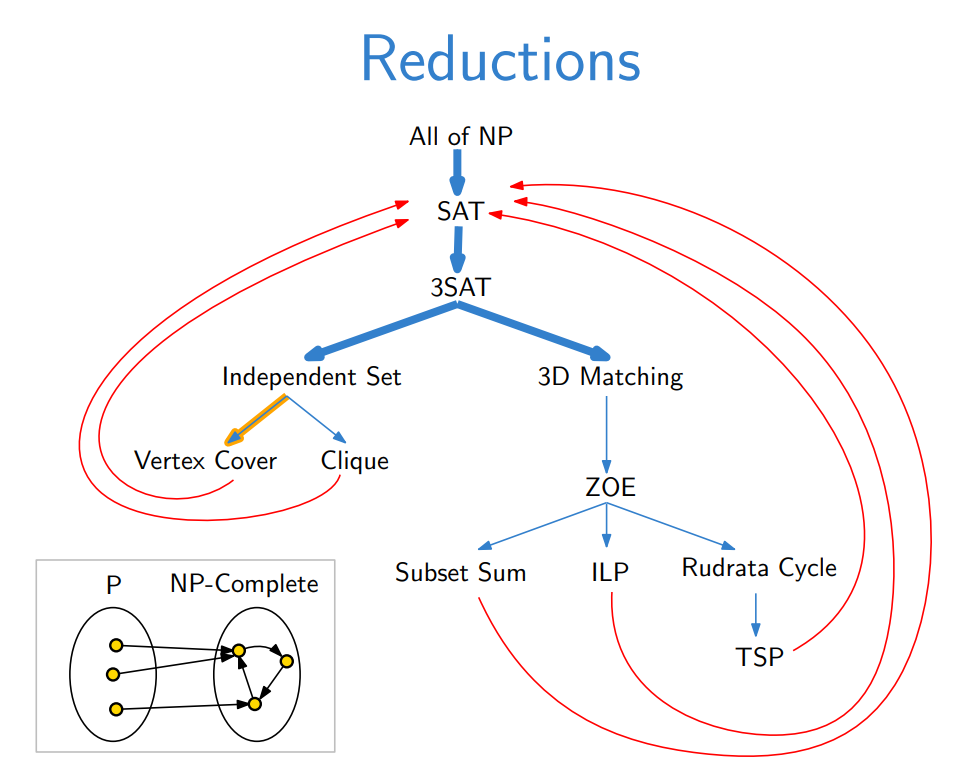
위 그림을 보면, 모든 Search Problem, 즉 $\textbf{NP}$ 문제가 <SAT>로 reduction 되는 걸 볼 수 있다. 따라서 <SAT>는 $\textbf{NP-complete}$다. 그외에 우리가 살펴봤던 <3-SAT>, <Independent Set Problem> 등이 일련의 Reduction을 거쳐서 다시 <SAT>로 환원된다. 따라서 위 그림에 등장하는 Search Problem 모두 $\textbf{NP-complete}$다!
사실 위 그림을 진정으로 이해하려면, <Reduction>이 composition property를 갖는다는 사실을 알아야 한다.
For reduction,
If $A \rightarrow B$ and $B \rightarrow C$, then $A \rightarrow C$
<Reduction>의 composition property를 할용하면, “All NP → ???”를 증명하지 않고, “All NP → SAT”를 보인 후에 “SAT → ???”를 보이면, “All NP → ???”를 증명하는데 충분하기 때문이다!
본인 교재에서는 $\textbf{NP-complete}$를 NP problem의 reduction 가능성으로 정의 내렸다. 그러나 다른 자료에서는 $\textbf{NP-hard}$를 정의하고, 이를 활용해 $\textbf{NP-complete}$를 정의한다. 그래서 아래와 같은 Complexity Space를 제대로 이해하려면, “NP-complete and NP-hard” 포스트를 살펴보도록 하자. 또는 Reduction의 케이스들을 먼저 살펴보고 $\textbf{NP-complete}$를 이해해도 좋다.

자! 이제 몇 편의 포스트에 걸쳐서 이제껏 살펴봤던 $\textbf{NP}$ 문제들이 어떻게 서로 <Reduction> 되는지 살펴볼 것이다.
