Local Search
2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :) 전체 포스트는 Algorithm 포스트에서 확인하실 수 있습니다.
이전의 두 포스트, <Backtracking>과 <Branch-and-Bound>는 Exhausitive Search 방식이었다. 이번에 살펴보는 <Local Search>는 Heuristic Algorithm의 일종으로 “Optimality of the solution”를 희생해 빠르게 solution을 찾는 기법이다.
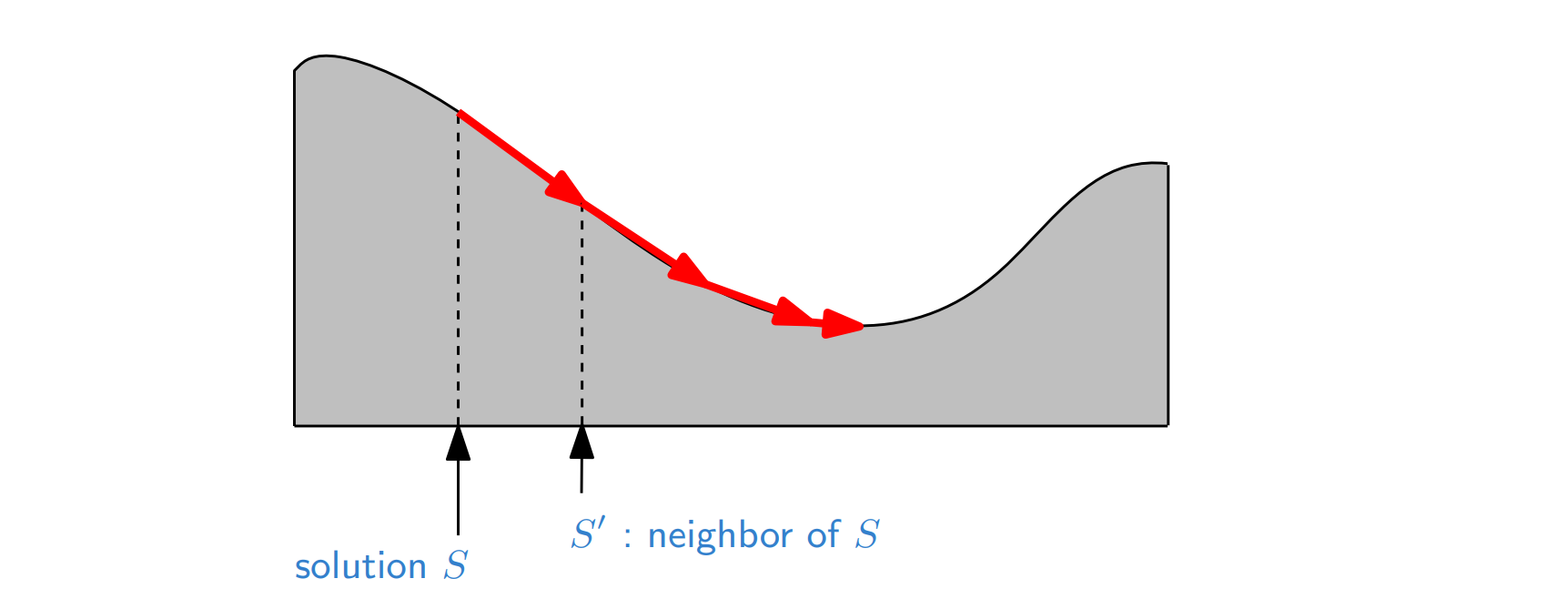
<Local Search>는 현재의 partial solution에서 가까운 이웃 solution을 탐색해 그 중 가장 좋은 녀석으로 partial solution을 갱신하는 기법이다.
incremental process of introducing small mutations and keeping them if they work well!
이번에도 <TSP> 문제를 바탕으로 <Local Search>를 좀더 이해해보자.
TSP with Local Search
우선 여기서의 <TSP> partial solution은 어떤 Hamilton Cycle이다. 그래프가 Complete Graph라면, 당연히 Hamilton Cycle이 존재 할 것이니 일단 하나를 만들어 둔다.

그리고 이 partial solution을 아주 약간 수정해 neighborhood solution을 만든다. 서로 다른 두 투어(tour)가 서로 얼마나 가까운지, 서로 이웃인지를 어떻게 정의할까?
우리는 cycle을 다루고 있기 때문에, 두 cycle이 하나의 edge만 다를 순 없다. 적어도 2개의 edge를 바꿔줘야 새로운 cycle을 만들 수 있기 때문이다. 그래서 우리는 “2-change neighborhood”라고 2개의 edge가 바꿔 partial solution의 neighborhood solution을 생성하겠다.
Let $s$ be any initial solution.
while there is some solution $s’$ in the neighborhood of $s$
for which $\text{cost}(s’) < \text{cost}(s)$: replace $s$ by $s’$.
return $s$.
이 방식은 정말 빠르다. 어떤 partial solution이라도 2-change neighborhood는 $O(n^2)$ 만큼 존재하기 때문이다. 그러나 iteration을 ‘언제’ 멈춰야 할지는 정해지지 않았다. 운이 안 좋으면 평생 iteration을 해도 원하는 solution에 도달하지 못할 수 있다. 이것이 <Local Search>의 단점인데, 탐색을 통해 찾은 final solution이 optimal solution임을 단언할 수 없다. 그것은 단지 local optimal solution일 뿐이다!

이것을 해결하고 싶다면, 이웃의 정의를 좀더 넓게 잡으면 된다. 3개의 edge가 다른 녀석도 이웃으로 보고, 4개의 edge도 이웃으로 본다면, 더 넓은 범위를 후보로 잡아 주변 녀석과 비교해 좀더 좋은 녀석으로 solution을 갱신할 수 있을 것이다.
그러나 이렇게 이웃의 정의를 확장한다면, 한 iteration에서 탐색해야 할 이웃의 수가 늘어가게 된다. 3-change neighborhood라면 $O(n^3)$의 비용이 들게 된다. 그래서 optimality와 complexity 사이의 적절한 수준으로 타협해 Neighborhood-ness를 결정하도록 하자.
Dealing with local optima: Simulated Annealing
<Local Search>는 solution의 optimality를 보장하지 못한다는 단점이 있다. 이를 해결하고 싶다면, 단순히 새로운 starting point에서 <Local Search>를 수행해 새로운 solution을 얻는 방법이 있을 것이다. 그러나 무식하게 Restart 하는 것은 탐색 공간이 무지무지 크다면, 정말 많은 staring point가 존재하기 때문에 좋은 solution을 찾을 가능성이 크게 줄어든다.
그래서 약간의 포용성을 가진 <Local Search> 방식이 제시되었다. 여러번 Restart 하는 대신 확률적으로 bad solution을 탐색함으로써 Restart의 랜덤성을 확보한다.
Occasionally allow moves that actually increase the cost, in the hope that they will pull the search out of dead ends.
Let $s$ be any starting solution.
repeat
randomly choose a solution $s’$ in the neighborhood of $s$
if $\text{cost}(s’) < \text{cost}(s)$:
replace $s$ by $s’$
else:
replace $s$ by $s’$ with probability $p$
return $s$.
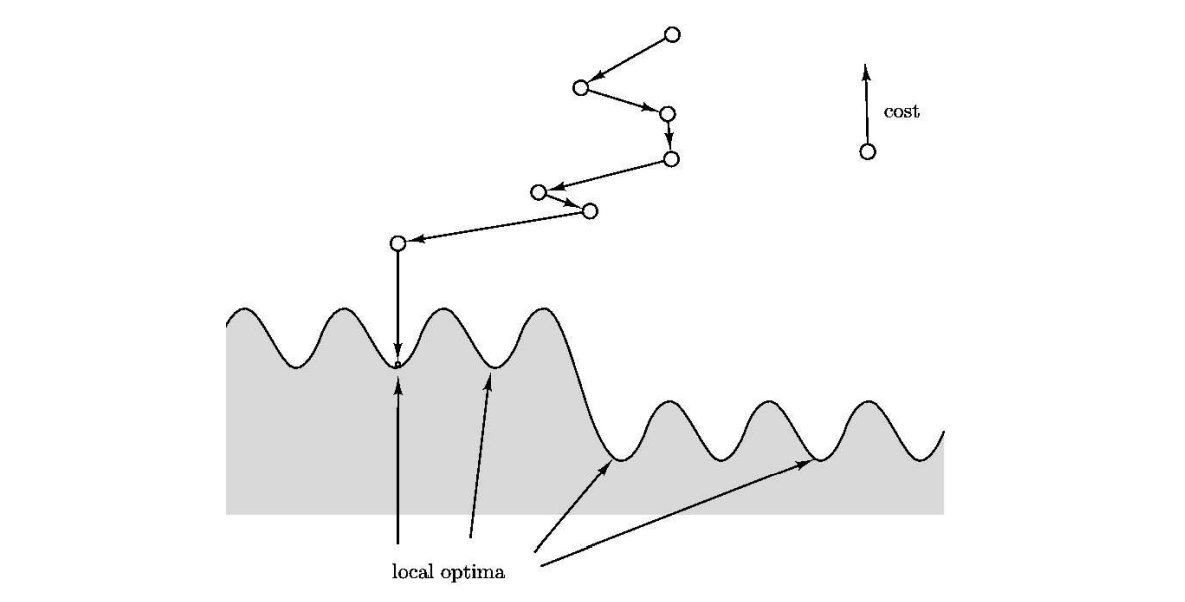
그러나 이렇게 할 경우, (정말 운이 나쁘면) global solution 바로 앞에서 randomly pick한 neighbor로 가버릴 수 있을 것이다. 이런 상황을 방지하기 위해 iteration을 진행할 수록 probability $p$의 값을 줄여 오직 $\text{cost}(s’) < \text{cost}(s)$만 허용하도록 <Local Search>를 설계할 수 있다. 이것을 위해 cost difference $\Delta$와 temperature $T$를 도입한다.
Let $s$ be any starting solution.
repeat
randomly choose a solution $s’$ in the neighborhood of $s$
if $\Delta = \text{cost}(s’) - \text{cost}(s) < 0$:
replace $s$ by $s’$
else:
replace $s$ by $s’$ with probability $e^{-\Delta / T}$
return $s$.
cost difference $\Delta$는 iteration을 돌면서 동적으로 정해지는 값이다. $\Delta < 0$이면, $\text{cost}$가 감소하므로 그걸 선택한다. $\Delta > 0$라면 bad solution이지만, 확률 $0 \le p = e^{-\Delta / T} \le 1$에 따라 accept 또는 reject 한다.
만약 $T = 0$라면, $e^{-\Delta / T} \rightarrow e^{-\inf} = 0$이기 때문에 pure한 <Local Search>와 같다. 만약 $T > 0$라면, $0 < e^{-\Delta / T} < 1$로 가끔식 bad solution으로 탐색하게 된다.
그런데 temperature $T$로 어떤 값을 설정해야 할까? 가장 간단한 방법은 처음엔 큰 값의 $T$로 시작해서 iteration을 돌 때마다 $T \leftarrow T - 1$을 해 $T$ 값을 점점 줄여 0으로 만드는 것이다. 이것은 <Local Search> 초기에는 자유롭게 search space를 돌아다니며 local optima에서 벗어나려고 한다. 그러나 $T$ 값이 0으로 수렴하기 때문에 점차 strict <Local Search>를 수행하게 된다.
위와 같은 방식을 <Simulated Annealing; 담금질 기법>라고 하는데, “Annealing”은 고온의 금속을 서서히 식히는 방식이라고 한다. 물리학(physics)의 콘셉트에서 영감을 받은 기법인데, 입자들이 고온에선 기체/액체 상태로 자유롭게 움직이지만, 열이 식으면서 고체의 형태로 규칙적이고 결정의 형태로 변하는 것을 모사한 것이다.
이것으로 <알고리즘; Algorithm;>의 정규 수업에서 다룬 내용을 모두 살펴보았다 👏 다음 포스트에서 간단한 후기를 써보고자 한다 🙏
