Auto-Correlation: ACF & PACF
선행 개념
펼쳐보기
Definition. Variance
Definition. Covariance
Definition. Correlation
- Correlation은 $\left[ -1, 1 \right]$의 범위를 갖는다.
- 위와 같은 Correlation을 Pearson Correlation $r_{XY}$라고 한다.
Definition. Partial Correlation
where $e_{X}$ and $e_{Y}$ are residual of multiple regression fitting on $\mathbf{z}$.
Auto-Correlation이란?
시계열 데이터 $\{ s(t) \}$에서 $s(t)$는 이전의 타임 스텝의 $s(t-1)$, $s(t-2)$ 값에서 갑자기 크게 상승한다거나, 갑자기 크게 하락하는 일은 흔하지 않다.
Correlation $\text{Corr}(X, Y)$은 본래 서로 다른 두 Random Variable $X$, $Y$의 상관성을 보기 위한 지표이다. 그런데, 시계열 데이터에선 자신과 이전의 값 사이에 상관성을 보기 위해 Auto-Correlation $\text{Corr}(s(t), s(t-1))$를 구한다.
\[\text{Corr}(s(t), s(t-1)) = \frac{\text{Cov}(s(t), s(t-1))}{\sqrt{\text{Var}(s(t))} \sqrt{\text{Var}(s(t-1))}} = \frac{\text{Cov}(s(t), s(t-1))}{\text{Var}(s(t))}\]Auto-Correlation의 수식과 컨셉은 별로 어렵지 않다. 시계열 데이터를 $t$와 $t-1$로 표현하면 아래와 같은데,
| $t$ | $s(t)$ | $s(t-1)$ |
|---|---|---|
| 1 | 11 | 10 |
| 2 | 12 | 11 |
| 3 | 14 | 12 |
| 4 | 16 | 14 |
| 5 | 20 | 16 |
시계열 $s(t)$가 위와 같은 패턴을 보인다면, Auto-Corrrelation $\text{Corr}(s(t), s(t-1))$는 양(+)의 부호를 가질 것이다.
Auto-Correlation 수식을 좀더 일반화해서 Auto-Correlation Function, ACF로 표현하기도 한다. 이전 $k$ 스텝과의 상관성을 보기 위한 ACF $\text{ACF}(k)$는 아래와 같이 정의한다.
\[\text{ACF}(k) = \frac{\text{Cov}(s(t), s(t-k))}{\text{Var}(s(t))}\]Example: goog200
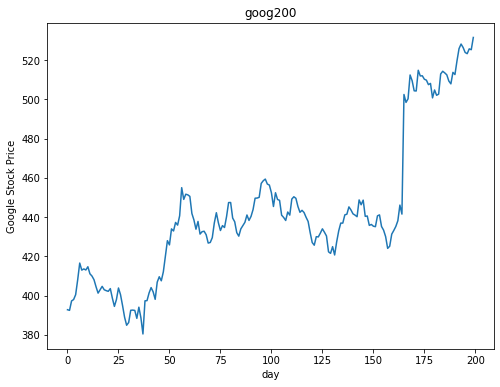
goog200이라는 시계열 주가 데이터에서 ACF를 구해보면 아래와 같다.
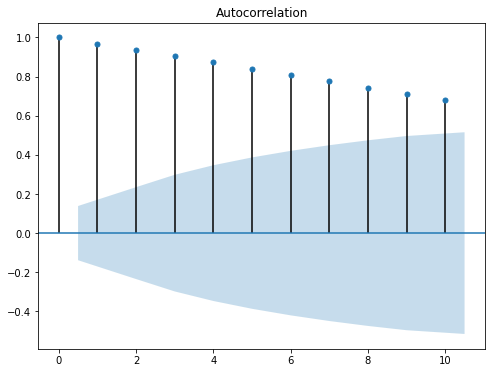
전반적으로 이전의 데이터에 높은 양(+)의 상관성을 보이는 것을 알 수 있다.
Partial ACF
$\text{ACF}(k)$는 $s(t)$와 $s(t-k)$, 두 값의 상관성을 출력한다. 그러나 그 사이에 있는 $s(t-1)$부터 $s(t-(k-1))$의 영향력이 존재하지 않았을까? 🤔
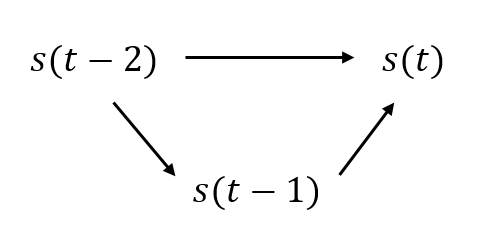
$s(t)$와 $s(t-1)$가 상관성이 있다면, $s(t-1)$와 $s(t-2)$도 상관성이 있을 것이다. 그렇다면, $s(t)$와 $s(t-2)$도 상관성이 있을 것이라는게 자연스럽게 유도된다.
<Partial Correlation>라는 개념이 있다. 자세한 내용은 “Partial Correlation” 포스트에 적어뒀지만, 간단히 말해보자면. 여러 개의 독립변수가 있고, 각 독립변수 사이에 어느정도의 Correlation이 있을 때, 그런 독립변수 사이의 상관성을 배제하고 오직 독립변수 단독의 종속변수에 대한 Correlation을 측정하는 방법이다.
Partial ACF $\text{PACF}(k)$ 역시 $s(t)$와 $s(t-k)$의 상관성을 측정한다는 것은 $\text{ACF}(k)$와 동일하다. 그러나 $\text{PACF}(k)$는 $s(t)$와 $s(t-k)$ 사이의 $s(t-1)$부터 $s(t-(k-1))$의 영향을 배제하고 상관성을 측정한다!
Example
다시 goog200 시계열 주가 데이터를 활용해 PACF 그래프를 그려보자.
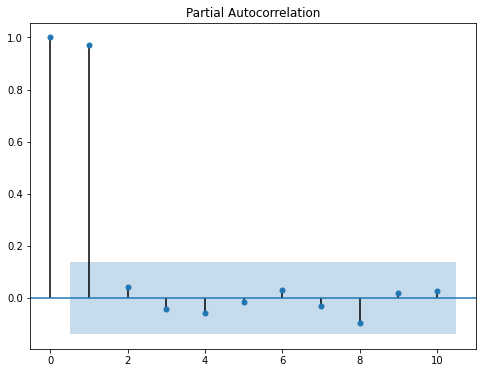
이번에는 ACF와 다르게, $\text{PACF}(1)$에서만 큰 상관성을 보였다. 이것을 통해 $S(t)$와 $S(t-1)$가 좀더 유의한 상관관계가 있을 거라고 생각할 수 있다! 😀
Derivation
PACF를 유도하는 것은 Partial Correlation $\rho_{XY\cdot Z}$를 유도하는 것과 동일하다. 영향을 배제하고자 하는 독립변수에 대해 Linear Regression Fitting을 하고, 잔차(residual)에 대해 Correlation을 구해주면 된다! 👏
Simple Case
우선 간단한 $k=2$인 경우부터 유도해보자. 우리는 $\text{PACF}(2)$, 즉 $s(t)$와 $s(t-2)$의 Partial Auto-Correlation을 구하고자 한다.
먼저 아래와 같이 Linear Regression Fitting을 한다.
\[\begin{aligned} w^{\ast}_{s(t)} &= \underset{w}{\text{argmin}} \left\{ \sum_{i} = (s(i) - w \cdot s(i-1))^2 \right\} \\ w^{\ast}_{s(t-2)} &= \underset{w}{\text{argmin}} \left\{ \sum_{i} = (s(i-2) - w \cdot s(i-1))^2 \right\} \end{aligned}\]개인적으로 PACF의 식을 이해하려고 할 때, 이해가 안 되는 부분이 $s(t)$에서는 $s(t-1)$에 대해 Fitting 했는데, $s(t-2)$에서 그 이전 스텝인 $s(t-1)$로 Fitting 하는 것이었다. $s(t-2)$와 $s(t-3)$로 Fitting 하는게 아니라 말이다!
사실 이건 <Partial Correlation>의 정의를 이해하면서 해소되었다. $s(t)$와 $s(t-2)$의 Partial Correlation을 구하기 위해 그 사이의 다른 독립변수인 $s(t-1)$의 영향을 배제하는 과정이므로, 두 변수에서 $s(t-1)$에 대해 Fitting 하는 것이 맞다! 😀
이제 잔차(residual)을 구하면,
\[\begin{aligned} e_{s(t), i} &= s(i) - w^{\ast}_{s(t)} \cdot s(i-1) \\ e_{s(t-2), i} &= s(i-2) - w^{\ast}_{s(t-2)} \cdot s(i-1) \end{aligned}\]마지막으로 잔차에 대한 Correlation을 구해주면 된다.
\[\text{PACF}(k) = \text{Cor} \left(e_{s(t)}, e_{s(t-2)} \right)\]Generalization
이제 일반적인 $\text{PACF}(k)$의 수식에 대해 유도해보자. 이제는 <Partial Correlation>이라는 방식에 익숙하리라 믿고, 바로 수식을 써보겠다.
Definition. Partial ACF
where $\hat{s(t)}$ is a linear combination of $\left\{ s(t-1), s(t-2), …, s(t-(k-1))\right\}$ that minimize the mean squared error of $s(t)$ and $s(t-k)$ respectively.
맺음말
ACF와 PACF는 시계열 데이터를 EDA 하는 과정에서 사용하는 기법 중 하나다. ACF, PACF 그래프를 보고, 어떤 시계열 모델을 쓸지 결정하게 된다.
ACF, PACF를 제대로 쓰려면 어떤 시계열 모델들이 있는지를 먼저 알아야 한다. 아래의 모델들을 먼저 공부하고 오자.
- AR(Auto-Regressive) Model
- MA(Moving Average) Model
- ARMA Model
