수열의 극한을 판정하는 법

June 7, 2024 2 minute read

복수전공하고 있는 수학과의 졸업시험을 위해 학부 수학 과목들을 다시 공부하고 있습니다. 미적분학 포스트 전체 보기

개인적으로 미적1의 마지막 챕터인 수열과 급수에 대한 부분이 미적1에서 제일 헷갈리는 부분이라고 생각합니다. 이번 기회에 해당 내용을 블로그 포스트로 꼼꼼히 정리해보았습니다 😁

함수의 극한으로 수열의 극한 구하기

수열 ${ a_n }$에 대해서 그에 대응하는 함수 $f(x)$를 정의한다. 이때, $f(n) = a_n$라고 정의한다.

만약 함수 $f(x)$의 극한이 $L$로 수렴한다면, 수열 ${ a_n }$의 극한도 $L$로 수렴한다.

세 수열 ${ a_n }$, ${ b_n }$, ${ c_n }$가 있을 때, 어떤 큰 $n$에 대해서 $a_n \le b_n \le c_n$를 만족한다고 하자. 그러면,

만약 수열 ${ a_n }$이 $L$로 수렴 한다면, 어떤 continuous 함수 $f(x)$에 수열을 합성한 $f(a_n)$은 $f(L)$로 수렴한다.

예를 들어, ${ \sqrt{(n+1)/n} }$라는 수열은 $(n+1)/n \rightarrow 1$라는 사실을 알고 있고 $f(x) = \sqrt{x}$로 연속 함수 이기 때문에 $\sqrt{a_n} \rightarrow 1$로 수렴한다.

If a sequence ${ a_n }$ is both bounded and monotonic, then the sequence converges.

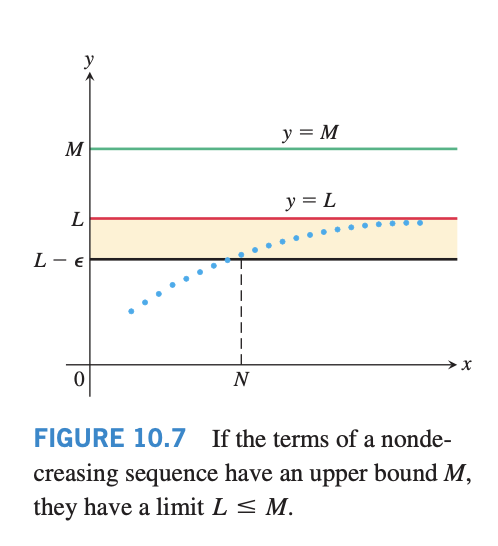
그럼으로 보면 요런 느낌.

If $\sum_{n=1}^{\infty} a_n$ converges, then $a_n \rightarrow 0$.

대우 명제를 사용하면, 급수가 발산 하는지도 테스트 할 수 있다.

이때, 역 명제는 성립하지 않는다. 수열이 $a_n \rightarrow 0$를 만족하더라고 급수는 발산할 수도 있다. 그 예시가 바로 조화(harmonic) 급수!!

\[\sum_{n=1}^{\infty} \frac{1}{n} = \infty\]

수열에 대한 극한을 판정하는 것은 생각보다 쉽다!! 다음은 급수(series)에 대한 극한을 판정하는 방법들을 살펴보자!