Sequence and Series: Problem Solving

복수전공하고 있는 수학과의 졸업시험을 위해 학부 수학 과목들을 다시 공부하고 있습니다. 공부하면서 재밌어 보였던 문제들과 풀이들을 모아서 정리한 포스트 입니다. 미적분학 포스트 전체 보기

The zipper theorem

If ${ a_n }$ and ${ b_n }$ both converge to $L$, then the sequence

\[a_1, b_1, a_2, b_2, ..., a_n, b_n, ...\]

converges to $L$.

일단 zipper 수열을 정의하면 아래와 같다.

\[c_n = \begin{cases} a_n & n \text{ is odd} \\ b_n & n \text{ is even} \\ \end{cases}\]

이제 $n$이 홀수/짝수인 경우를 생각해보자.

<$n = 2m + 1$: odd>

\[\lim_{m \rightarrow \infty} c_{2m + 1} = \lim_{m \rightarrow \infty} a_m = L\]

<$n = 2m$: even>

\[\lim_{m \rightarrow \infty} c_{2m} = \lim_{m \rightarrow \infty} b_m = L\]

즉, 홀수/짝수 두 경우에 대해서 둘다 극한이 $L$로 수렴하므로 zipper 수열도 수렴한다.

A recursive definition of $\pi/2$

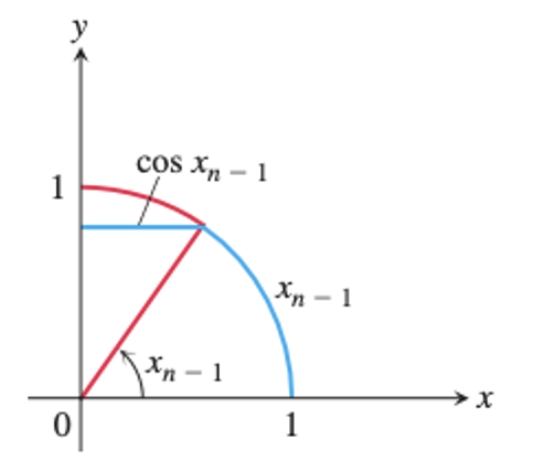
If you start with $x_1 = 1$ and define the subsequent terms of ${ x_n }$ by the rule $x_n = x_{n-1} + \cos x_{n-1}$, then show the sequence converges rapidly to $\pi/2$.

Thomas Calculus 13th ed. - Example Problem

연습문제에선 수열을 ${ x_n }$으로 표현했는데, 좀더 이해가 쉽도록 ${ \theta_n }$으로 바꿔서 표현하겠다.

일단 위의 다이어그램 상으로 $\theta_n$의 값은 파란 선으로 그려진다. 이것은 (1) 호의 길이와 (2) x축에 평행인 선분으로 이뤄지는데,

• (1) 단위원 위에서 각 $\theta_{n-1}$가 이루는 호의 길이가 $1 \cdot \theta_{n-1}$이 되고,
• (2) x축에 대한 정사영한 길이가 $\cos \theta_{n-1}$이 되는 것이다.

이때, 빨간선으로 그려진 부분에 주목해보자. 정사영한 길이 (2)와 남은 각인 $\pi/2 - \theta_{n-1}$로 만든 호의 길이 사이에 아래의 부등식이 성립한다.

\[\cos \theta_{n-1} < \pi/2 - \theta_{n-1}\]

이 부등식에서 $\theta_{n-1}$에 대한 부분을 정리하면,

\[\begin{aligned} \theta_{n-1} + \cos \theta_{n-1} &< \pi/2 \\ \theta_n &< \pi / 2 \end{aligned}\]

즉, 수열 ${ \theta_n }$의 upper bound가 $\pi/2$임을 알 수 있다! 이때, 수열 ${ \theta_n }$는 증가 수열인데, 그 이유는 $\theta_n < \pi/2$이기 때문에 $0 < \cos \theta_n \le 1$ 범위를 갖게 되기 때문이다!

즉, 수열 ${ \theta_n }$이 증가수열이고, 상계를 가지기 때문에 “단조수렴정리”에 의해서 수열 ${ \theta_n }$이 수렴한다. 그리고 그 수렴값은 least upper bound인 $\pi/2$가 된다. $\blacksquare$

The Cantor set

닫힌 구간 $[0, 1]$을 3등분 하자. 가운데인 $(1/3, 2/3)$ 구간을 제거한다. 1/3 길이의 남은 두 구간에 대해서도 같은 작업을 하여 가운데 구간을 제거한다. 이 과정을 무한번 반복한다.

자세한 내용은 별도의 블로그 포스트에 적어뒀다. 링크

The Cauchy condensation test

Let ${ a_n }$ be a non-increasing sequence of positive terms that converges to $0$. Then $\sum a_n$ converges if and only if $\sum 2^n a_{2^n}$ converges.

For example, $\sum (1/n)$ diverges because $\sum 2^n \cdot (1/2^n) = \sum 1$ diverges.

이때, “condensation”은 응축이라는 뜻이다. 즉, 기존의 급수를 응축한 급수의 수렴/발산을 판정하는 것만으로도 기존 급수의 수렴/발산을 판정할 수 있다는 정리다.

Show $\sum a_n$ converges, then $\sum 2^n a_{2^n}$.

because, $a_n$ is non-increasing and positive sequence, blow inequality satisfies.

\[\begin{aligned} &a_1 + a_2 + a_3 + a_4 + a_5 + a_6 + a_7 + a_8 + \dots \\ &\ge a_1 + a_2 + (a_4 + a_4) + (a_8 + a_8 + a_8 + a_8) + \dots \\ &= a_1 + a_2 + 2 \cdot (a_4) + 2^2 \cdot (a_8) + \dots \\ &= a_1 + \sum 2^{n-1} a_{2^n} \end{aligned}\]

Due to upper bound $\sum a_n$ converges, so $a_1 + \sum 2^{n-1} a_{2^n}$ converges too. And, $\sum 2^{n-1} a_{2^n}$ converges, $\sum 2^n a_{2^n}$ converges also! $\blacksquare$

Show $\sum 2^n a_{2^n}$ converges, then $\sum a_n$.

이번에는 식을 다르게 묶어서 부등식 방향을 바꾸면 된다!

because, $a_n$ is non-increasing and positive sequence, blow inequality satisfies.

\[\begin{aligned} &a_1 + a_2 + a_3 + a_4 + a_5 + a_6 + a_7 + a_8 + \dots \\ &\le a_1 + (a_2 + a_2) + (a_4 + a_4 + a_4 + a_4) + (a_8 + \dots) \\ &= a_1 + 2 \cdot (a_2) + 2^2 \cdot (a_4) + \dots \\ &= a_1 + \sum 2^n a_{2^n} \end{aligned}\]

Due to upper bound $\sum 2^n a_{2^n}$ converges, so $\sum a_n$ converges too! $\blacksquare$