Parametric Equations: Problem Solving

복수전공하고 있는 수학과의 졸업시험을 위해 학부 수학 과목들을 다시 공부하고 있습니다. 공부하면서 재밌어 보였던 문제들과 풀이들을 모아서 정리한 포스트 입니다. 미적분학 포스트 전체 보기

The witch of Maria Agnesi

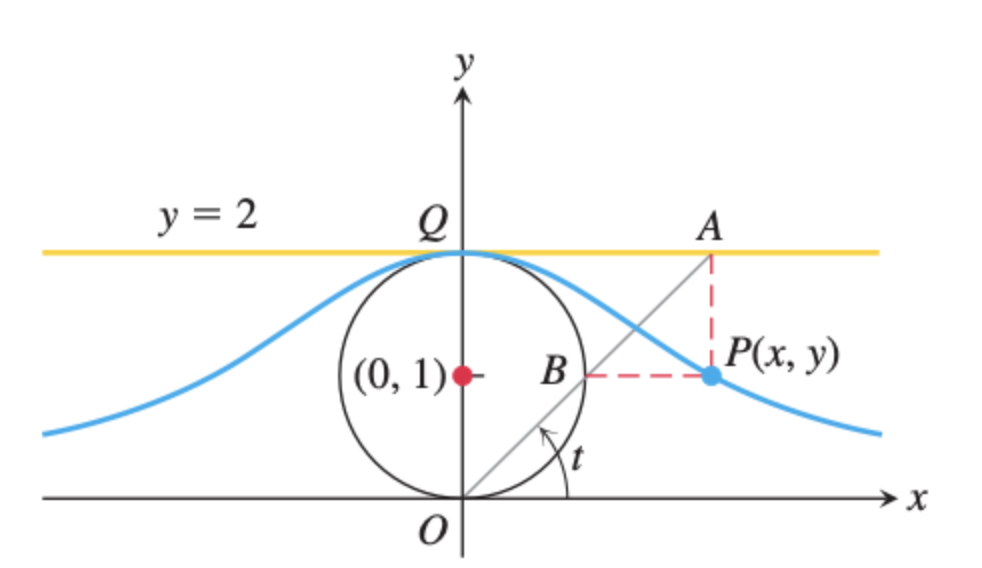Thomas Calculus 13th ed. - Example Problem

직전 $OA$와 $x$축이 이루는 각을 $t$라고 하자. 이때, 점 $P$의 자취에 대한 방정식을 구해야 한다. 점 $P$의 $x$ 좌표는 점 $A$의 $x$ 좌표값과 같고, 점 $P$의 $y$ 좌표는 직전 $OA$와 원이 만나는 점인 $B$의 $y$ 좌표값과 같다.

* 참고로 요 문제에 나온 마리아 아녜시(Maria Agnesi)는 실제 인물로, 18세기 이탈리아에서 활동한 여성 수학자이다.

일단 $P$의 $x$ 좌표값부터 구해보자. $OQ$의 길이가 $2$로 고정 되어 있으므로, $\tan t = 2/x$임을 이용해서 $x$ 값을 유도하면,

\[x = \frac{2}{\tan t} = 2 \cot t\]

점 $P$의 $y$ 좌표는 직각삼각형의 닮은 성질로 유도 되는 아래 성질을 활용해야 한다.

\[OA \cdot AB = (AQ)^2\]

그리고 $y = 2 - AB \cdot \sin t$라는 성질도 사용해야 한다. 이를 위해 $AB$에 대한 식을 유도해보자.

\[\begin{aligned} AB &= \frac{(AQ)^2}{OA} \\ &= \frac{x^2}{\sqrt{x^2 + 4}} \\ &= \frac{4 \cot^2 t}{\sqrt{4 \cot^2 t + 4}} \\ &= \frac{2 \cot^2 t}{\sqrt{\cot^2 t + 1}} \\ &= 2 \cot^2 \sin t \end{aligned}\]

이제 유도한 $AB$ 값을 대입하여 $y$ 좌표값을 유도하다.

\[\begin{aligned} y &= 2- 2 \cot^2 t \sin^2 t \\ &= 2(1 - \cos^2 t) \\ &= 2 \sin^2 t \end{aligned}\]

종합하면, 점 $P$에 대한 매개방정식은

\[P = \left( \frac{2}{\tan t}, \, 2 \sin^2 t \right)\]

Hypocycloid

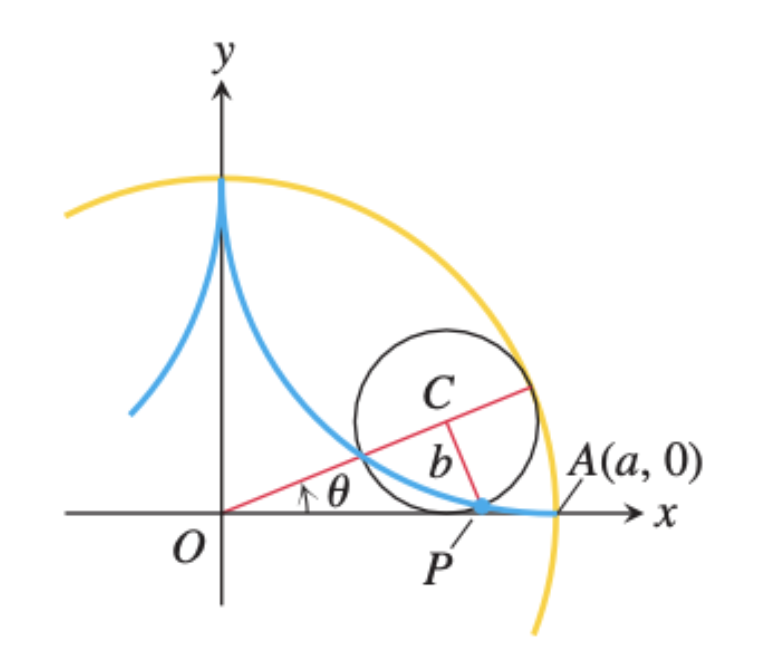Thomas Calculus 13th ed. - Example Problem

큰 원 안에 작은 원을 굴릴 때 생기는 원의 자취에 대한 방정식이다. 큰 원의 반지름은 $a$, 작은 원의 반지름을 $b$라고 하자.

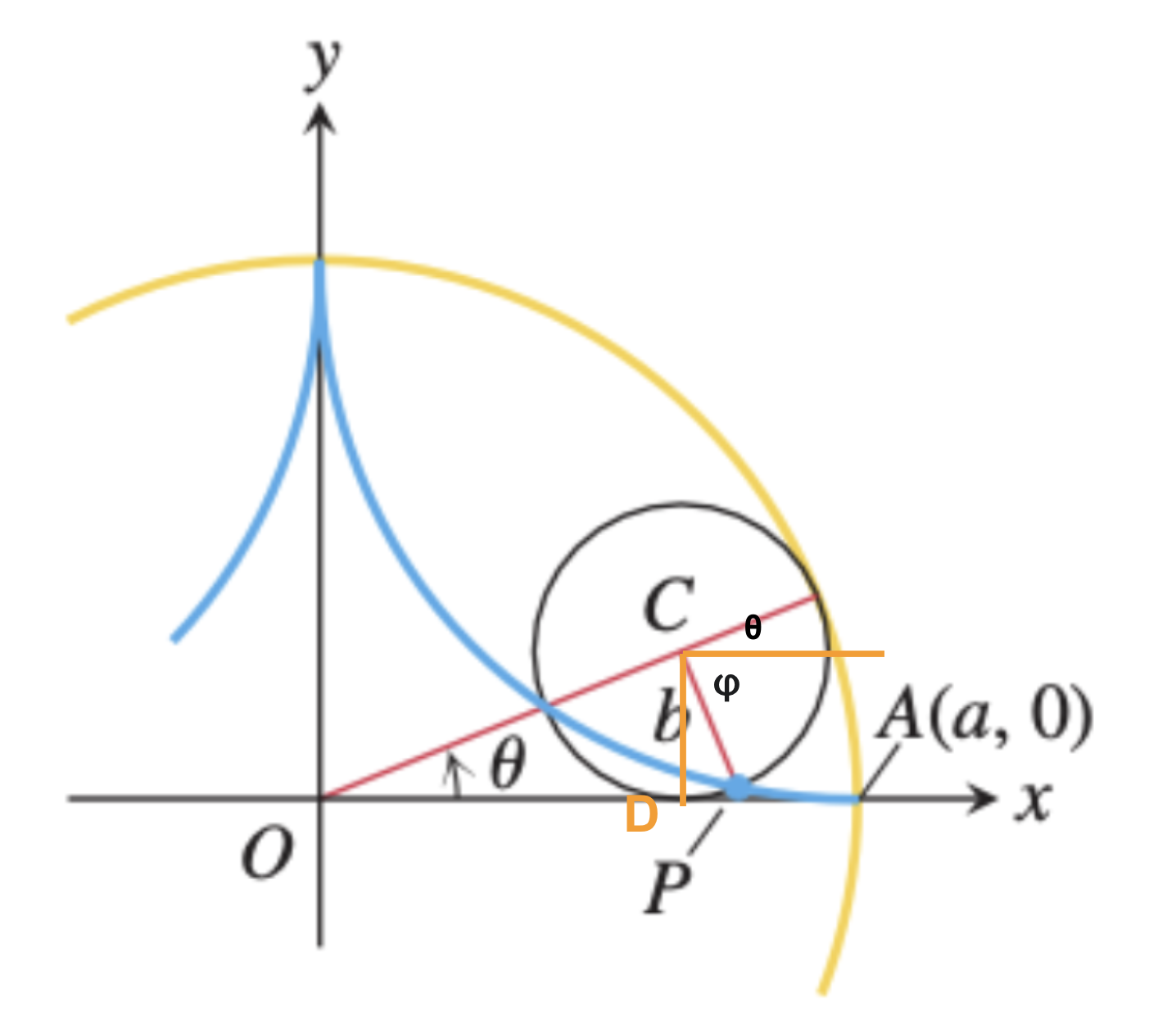
작은 원의 중심인 $C$의 좌표를 구해보자. $OC$의 길이가 $b - a$이므로 좌표값은 아래와 같다.

\[C = (x, y) = \left( (a - b) \sin \theta, \, (a-b) \cos \theta \right)\]

작은 원이 점 $A$에서 출발해서 움직인 각의 크기를 $\theta + \phi$라고 하자. 이때, $\phi > 0$가 되는데, 그 이유는 큰 원과 작은 원으로 둘의 반지름에 차이가 있기 때문이다. 그래서 작은 원이 큰 원보다 더 많은 각을 움직이게 되는데, 그 크기를 $\phi$라고 하자.

이때, 점 $P$의 길이는 작은 원의 중심 $C$의 좌표에서 생각하면 아래와 같다.

\[\begin{aligned} x &= (a-b) \cos \theta + b \cos \phi \\ y &= (a-b) \sin \theta - b \sin \phi \end{aligned}\]

이$\theta$와 $\phi$ 사이에 아래의 관계식이 성립한다.

\[a \theta = b (\theta + \phi)\]

이것은 작은 원이 큰 원을 휩쓸고 지나간 거리이다. 이 두 값은 동일해야 한다. 이것을 기반으로 $\phi$를 $\theta$에 대해 정리하면 아래와 같다.

\[\phi = \frac{a - b}{b} \theta\]

따라서 점 $P$에 대한 매개방정식을 아래와 같다.

\[P = (x, y) = \left((a-b) \cos \theta + b \cos \left( \frac{a-b}{b} \, \theta \right)\,, (a-b) \sin \theta - b \sin \left( \frac{a-b}{b} \, \theta\right) \right)\]

Astroid

Public Domain, Link

이때, 큰 원과 작은 원의 반지름이 4배 차이가 난다면, 궤적이 Astroid가 된다. 이때의 매개방정식은 아래와 같다.

\[\begin{aligned} x &= a \cos^3 \theta \\ y &= a \sin^3 \theta \end{aligned}\]

왜 그런지는 식을 유도해보면 된다.

[$x$ 좌표]

\[\begin{aligned} x &= 3 b \cos \theta + b \cos (3 \theta) \\ &= 3 b \cos \theta + b \left( \cos \theta \cos 2 \theta - \sin \theta \sin 2 \theta \right) \\ &= 3 b \cos \theta + b \left( \cos \theta \cos^2 \theta - 3 \cos \theta \sin^2 \theta - 2 \sin^2 \theta \cos \theta \right) \\ &= 3 b \cos \theta + b \cos^3 \theta - 3b \cos \theta \sin^2 \theta \\ &= b \cos^3 \theta + 3b \cos \theta (1 - \sin^2 \theta) \\ & = b \cos^3 \theta + 3b \cos \theta \cos^2 \theta \\ &= 4b \cos^3 \theta = a \cos^3 \theta \end{aligned}\]

[$y$ 좌표]

\[\begin{aligned} y &= 3 b \sin \theta - b \sin (3 \theta) \\ &= 3 b \sin \theta - b \left( \sin \theta \cos 2 \theta + \cos \theta \sin 2 \theta \right) \\ &= 3 b \sin \theta - b \left( \sin \theta \cos 2 \theta + \cos \theta \sin 2 \theta \right) \\ &= 3 b \sin \theta - b \left( \sin \theta \cos^2 \theta - \sin^3 \theta + 2 \cos^2 \theta \sin \theta \right) \\ &= 3 b \sin \theta + b \sin^3 \theta - 3 b \sin \theta \cos^2 \theta \\ &= b \sin^3 \theta - 3 b \sin \theta (\cos^2 - 1) \theta \\ &= b \sin^3 \theta + 3 b \sin^3 \theta \\ &= 4b \sin^3 \theta = a \sin^3 \theta \\ \end{aligned}\]

Trochoids

Picture from Wolfram Mathworld

직선 위를 둥근 원이 둘러갈 때의 자취를 일반화한 것이 “Trochoids”이다. 원의 반지름을 $a$라고 하고, 원의 중심에서 뻗어나온 바큇살(spoke of wheel)의 길이를 $b$라고 하자. 이때, $a = b$인 상황이 많이 살펴본 “Cycloid”의 경우다. 이름은 그리스어로 “바퀴”를 뜻하는 trochos에서 유래했다고 한다.

매개방정식은 Cycloid의 것을 구했던 접근과 비슷하게 유도하면 된다.

\[\begin{aligned} x &= a \theta - b \sin \theta \\ y &= a - b \cos \theta \end{aligned}\]

Complete Elliptic Integral

아래와 같은 타원의 둘레를 계산해보자.

\[\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\]

이를 매개변수로 표현하면 아래와 같다.

\[\begin{aligned} x &= a \cos t \\ y &= b \sin t \end{aligned}\]

매개변수 방정식의 arc length를 계산하는 식에 따라 적분을 수행하면 아래와 같다.

\[P = 4 \cdot \int_0^{\pi/2} \sqrt{a^2 \sin^2 t + b^2 \cos^2 t} \, dt\]

식을 $a$를 기준으로 정리하면…

\[\begin{aligned} P &= 4 \cdot \int_0^{\pi/2} \sqrt{a^2 \sin^2 t + b^2 \cos^2 t} \, dt \\ &= 4 \cdot \int_0^{\pi/2} \sqrt{b^2 - (b^2 - a^2)\sin^2 t} \, dt \\ &= 4 \cdot \int_0^{\pi/2} b \sqrt{1 - \frac{(b^2 - a^2)}{b^2}\sin^2 t} \, dt \\ &= 4 \cdot \int_0^{\pi/2} b \sqrt{1 - k^2 \sin^2 t} \, dt \\ \end{aligned}\]

이때, $k$는 이심률(eccentricity)로 $0 \le k^2 \le 1$의 값을 갖는다.

요 타원 적분이 완전(complete)인 이유는 $0$부터 $\pi/2$까지 적분하기 때문이다. 만약 적분 범위가 $\pi/2$가 아니라 변수라면, 불완전 타원 적분이라고 한다.

\[F(\theta, k) = \int_0^{\theta} \sqrt{1 - k^2 \sin^2 t} \, dt\]

풀이

타원의 둘레를 구하는 적분은 non-elementary integral임이 알려져 있다. non-elementary integral이라고 해도 적분값은 계산할 수 있다!! 어떻게 구하는지 살펴보자.

$\sqrt{1 - x}$를 Generalized Binomial Theorem을 적용해 전개하면 아래와 같다.

\[\sqrt{1-x} = \sum_{n=0}^{\infty} \binom{1/2}{n} x^n = 1 - \frac{1}{2} x - \frac{1}{8} x^2 - \cdots\]

이걸 $\sqrt{1 - k^2 \sin^2 t}$에 적용해보자.

\[\sqrt{1-k^2 \sin^2 t} = 1 - \frac{1}{2} k^2 \sin^2 t - \frac{1}{8} k^4 \sin^4 t - \cdots\]

이제 $[0, \pi/2]$ 범위에 대해 적분해보자.

\[\begin{aligned} &\int_0^{\pi/2} \sqrt{1-k^2 \sin^2 t} \, dt \\ &=\int_0^{\pi/2} 1 - \frac{1}{2} k^2 \sin^2 t - \frac{1}{8} k^4 \sin^4 t - \cdots \, dt \\ \end{aligned}\]

이때, $n$이 짝수일 때, 적분 $\int_0^{\pi/2} \sin^n t \, dt$에 대해서 아래가 성립한다.

\[\begin{aligned} &\int_0^{\pi/2} \sin^n t \, dt \\ &= \frac{1 \cdot 3 \cdot 5 \cdots (n-1)}{2 \cdot 4 \cdot 6 \cdots n} \cdot \frac{\pi}{2} \\ &=\frac{(n-1)!!}{n!!} \cdot \frac{\pi}{2} \end{aligned}\]

적분식을 정리하면 아래와 같다.

\[\begin{aligned} &\int_0^{\pi/2} \sqrt{1-k^2 \sin^2 t} \, dt \\ &=\int_0^{\pi/2} 1 - \frac{1}{2} k^2 \sin^2 t - \frac{1}{8} k^4 \sin^4 t - \cdots \, dt \\ &= \frac{\pi}{2} - \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{\pi}{2}\cdot k^2 - \frac{1}{2 \cdot 4} \cdot \frac{1 \cdot 3}{2 \cdot 4} \frac{\pi}{2} k^4 - \cdots \\ &= \frac{\pi}{2} \left( 1 - \left( \frac{1}{2} \right)^2 k^2 - \left( \frac{1 \cdot 3}{2 \cdot 4} \right)^2 \frac{k^4}{3} - \cdots \right) \end{aligned}\]

위의 적분은 수렴하는지는 $k^2$의 등비 급수와 비교했을 때, 위의 적분이 더 가파르게 감소하기 때문에, Complete Elliptical Integral이 수렴한다고 말할 수 있다.

Limaçon Curve

By Sam Derbyshire - http://en.wikipedia.org/wiki/Image:EpitrochoidIn1.gif, CC BY-SA 3.0, Link

리마송(Limacon)은 프랑스어로 달팽이🐌라는 뜻이다. 곡선에 대한 정의는 아래와 같다.

고정된 원 $O_1$의 바깥쪽에 외접한, 반지름 길이가 같은 다른 한 원 $O_2$를 미끄러짐 없이 한 바퀴 굴렸다고 하자. 이때, 구르는 원의 중심에서 일정한 거리만큼 떨어져 있는 지점인 원의 바큇살이 구르는 원과 함께 움직이며 그리는 점의 자취.

Parametric Equation

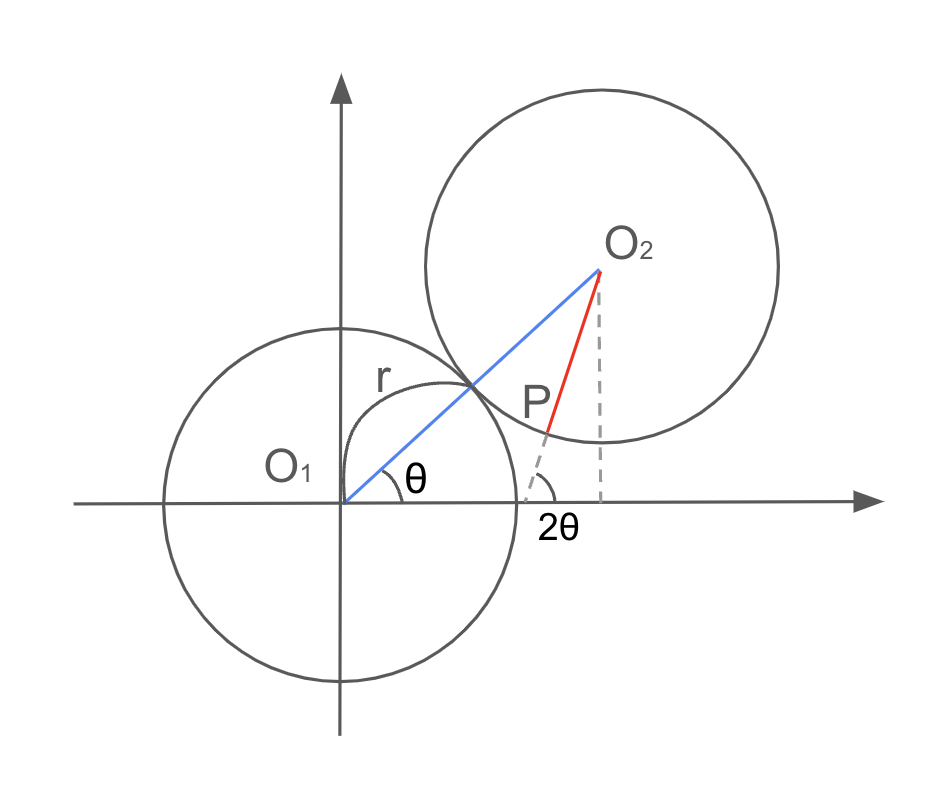
매개방정식의 꼴로 유도해보자. 계산의 편의를 위해 바깥 원의 바큇살을 원의 반지름과 같은 $R$이라고 하자.

점 $O_2$의 자취는 아래와 같다.

\[O_2 = (2R \cos \theta, \; 2R \sin \theta)\]

이때, 직선 $O_2 P$가 $x$축과 이루는 각도가 $2 \theta$이므로 점 $P$의 자취는 아래와 같다.

\[P = (2R \cos \theta - R \cos 2 \theta, \; 2R \sin \theta - R \sin 2 \theta)\]

위와 같이 기술해도 충분하다. 하지만 여기서 배각 $2 \theta$를 풀어서 $\theta$에 대해서로 바꿔보자.

<$x$ 좌표>

\[\begin{aligned} x &= 2R \cos \theta - R \cos 2 \theta \\ &= 2R \cos \theta - R \cos^2 \theta + R \sin^2 \theta \\ &= 2R \cos \theta - R \cos^2 \theta + R(1 - \cos^2 \theta) \\ &= 2R \cos \theta - 2R \cos^2 \theta + R \\ &= R + 2R \cos \theta (1 - \cos \theta) \end{aligned}\]

<$y$ 좌표>

\[\begin{aligned} y &=2R \sin \theta - R \sin 2 \theta \\ &= 2R \sin \theta - 2R \sin \theta \cos \theta \\ &= 2R \sin \theta (1 - \cos \theta) \end{aligned}\]

어떤 자료에서는 점 $P$의 자취가 원점 $O$부터 시작하도록 기술하기 위해 $x$ 축에 대해서 평행이동 시키는 경우가 있다. 이 경우, 방정식이 아래와 같이 기술된다.

\[P' = (2R \cos \theta (1 - \cos \theta), \; 2R \sin \theta (1 - \cos \theta))\]

요렇게 원점 $O$에서 시작하는 리마송 곡선은 뒤에서 극좌표 방정식으로 표현할 때 사용하게 된다.

위의 유도에서는 바큇살의 길이가 원의 반지름인 $R$과 같다고 두었다. 바큇살의 길이가 $R$이 아닌 $r$라고 한다면, 식은 아래와 같다.

\[\begin{aligned} P &= (2R \cos \theta - r \cos 2\theta, \; 2R \sin \theta - r \sin 2\theta) \\ &= (r + 2 \cos \theta(R - r \cos \theta), \; 2 \sin \theta (R - r \sin \theta)) \end{aligned}\]

Polar Equation

매개변수 방정식으로 표현한 리마송 곡선을 극좌표 방정식으로 표현해보자. 이때, 원점 $O$에서 시작하는 리마송 곡선을 표현한 방정식을 사용하면, 식이 훨씬 간편하게 정리된다.

\[\begin{aligned} r^2 &= x^2 + y^2 \\ &= \left( 2R \cos \theta \cdot (1 - \cos \theta) \right)^2 + \left( 2R \sin \theta \cdot (1 - \cos \theta) \right)^2 \\ &= 4 R^2 \cdot (1 - \cos \theta)^2 \end{aligned}\]

즉, 극좌표 방정식을 표현하면 $r = 2 R \cdot (1 - \cos \theta)$로 표현된다.

By Mktyscn - Made by Mktyscn using a custom C program and Windows Notepad, CC BY-SA 3.0, Link

만약 바큇살의 길이가 $r$라고 하면, 극좌표식은 아래와 같다.

\[r = 2R - 2r \cos \theta\]

$R$과 $r$의 대소 관계에 따른 리마송 곡선의 모양이 어떻게 달라지는지, 위의 그림을 기준으로 이해해보면

• $R > r$
  • 원점 $O$를 지나지 않는다.
• $R = r$
  • 원점 $O$를 지나간다.
  • 심장형 곡선
• $R < r$
  • 원점 $O$를 지나간다.
  • 원점 $O$를 지나면서 매듭이 생긴다.

Cardioid

By Ag2gaeh - Own work, CC BY-SA 4.0, Link

심장형 곡선(cardioid)는 리마송 곡선의 특수한 경우로, 원의 반지름과 바큇살의 반지름의 길이가 같은 경우다: $R = r$.

매개변수 방정식으로는

\[\begin{aligned} x &= 2R \cos \theta (1 - \cos \theta) \\ y &= 2R \sin \theta (1 - \cos \theta) \end{aligned}\]

극좌표 방정식으로는

\[r = 2R (1 - \cos \theta)\]

Lissajous Curve

By Vhastorga - Own work, CC BY-SA 4.0, Link

리사주 곡선(Lissajous Curve)는 두 사인파 곡선이 수평축과 수직축을 이룰 때, 이 들의 위상차(phase difference), 주파수비에 따라 그려지는 곡선을 말한다.

By Thierry Dugnolle - Own work, CC BY-SA 4.0, Link

가장 익숙한 형태로는 원형(Circle)으로 $x = \cos t$, $y = \sin t$로 두 곡선은 $\pi/2$의 위상차에 같은 주파수비를 가지고 있다.

리사쥬 곡선을 이루는 두 사인파의 주바수비를 쉽게 확인하는 방법은 $x$축과 $y$축에서 $x=1$, $y=1$ 지점에 곡선이 몇번 접하는지 세어보면 된다.

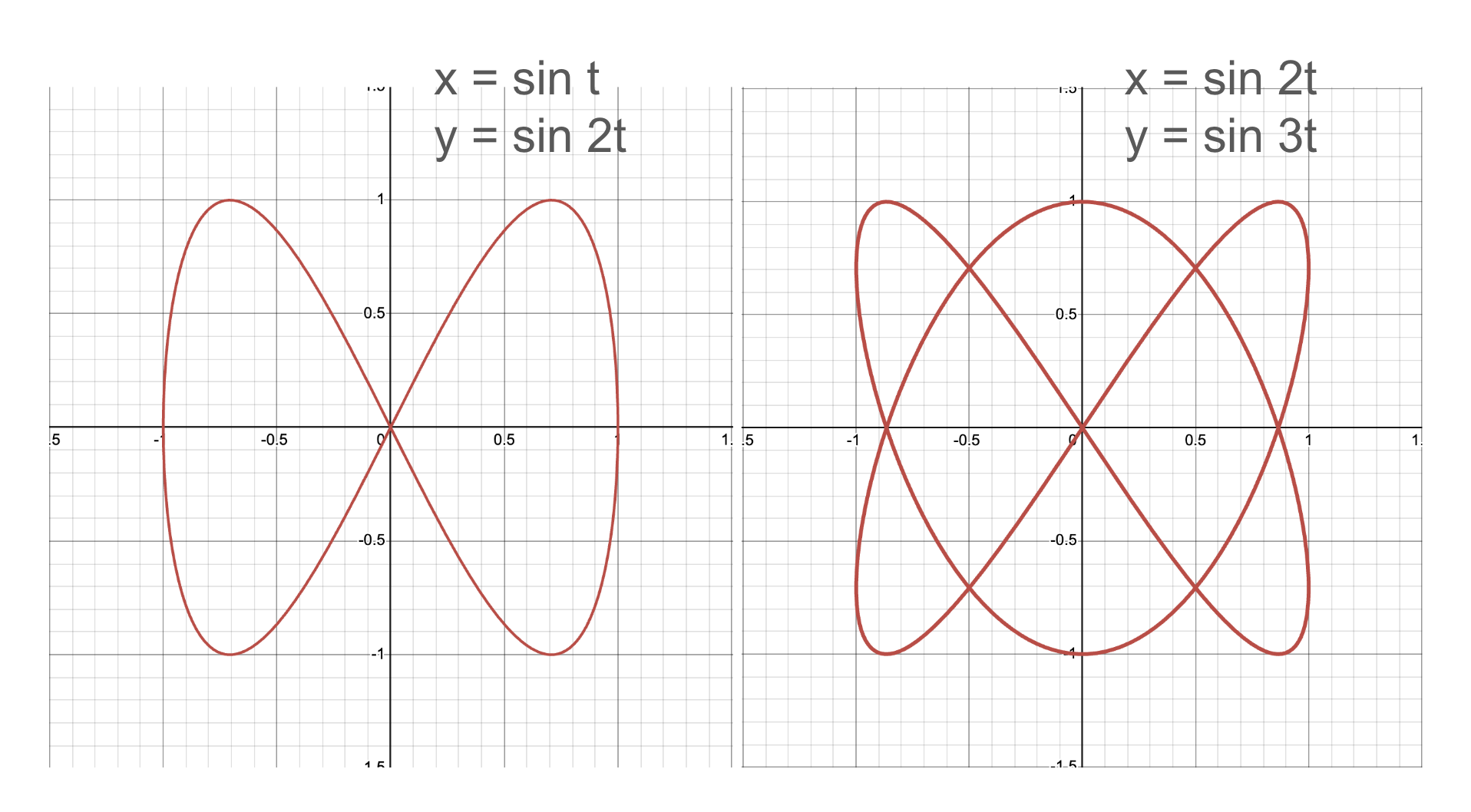
첫번째 곡선은 $x=1$에 1번 접하고 $y=1$에 2번 접하므로, $x$ 사인파와 $y$ 사인파의 주파수 비율이 1:2를 이룬다.
두번째 곡선은 $x=1$에 2번 접하고 $y=1$에 3번 접하므로, $x$ 사인파와 $y$ 사인파의 주파수 비율이 2:3을 이룬다.

Nephroid

By Sam Derbyshire at the English Wikipedia, CC BY-SA 3.0, Link

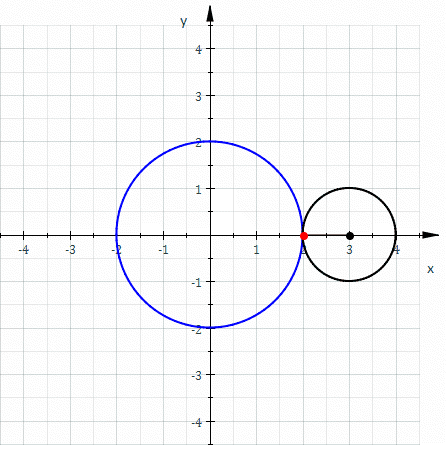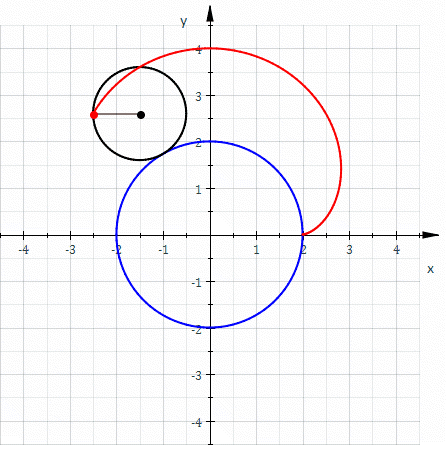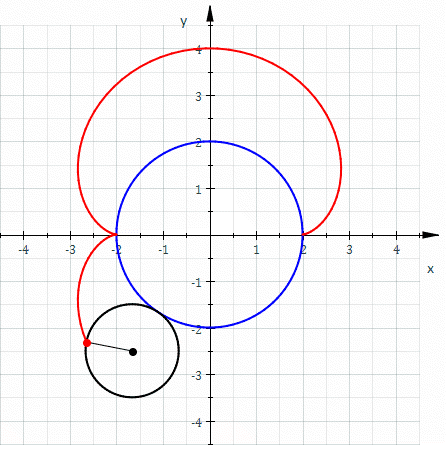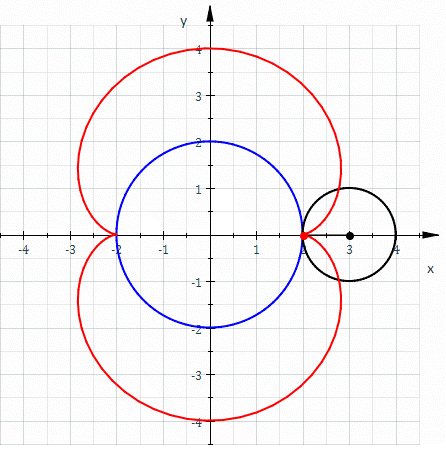
콩팥형 곡선(Nephroid, 네프로이드)는 궤적의 모양이 콩팥과 같이 생긴 곡선이다.

고정된 원의 바깥을 다른 원이 구르는 궤적이라는 점에서 앞에서 살펴본 리마송(Limaçon) 곡선과 비슷하다. 그러나, 리마송 곡선은 고정된 원과 구르는 원의 반지름이 정확히 같았고, 네프로이드 곡선은 고정된 원과 구르는 원의 반지름 비율이 “2:1“이다.

Parametric Equations

매개변수 방식을 유도하면 아래와 같다.

\[\begin{aligned} x &= 3 r \cos \theta - r \cos 3\theta \\ y &= 3r \sin \theta - r \sin 3\theta \end{aligned}\]

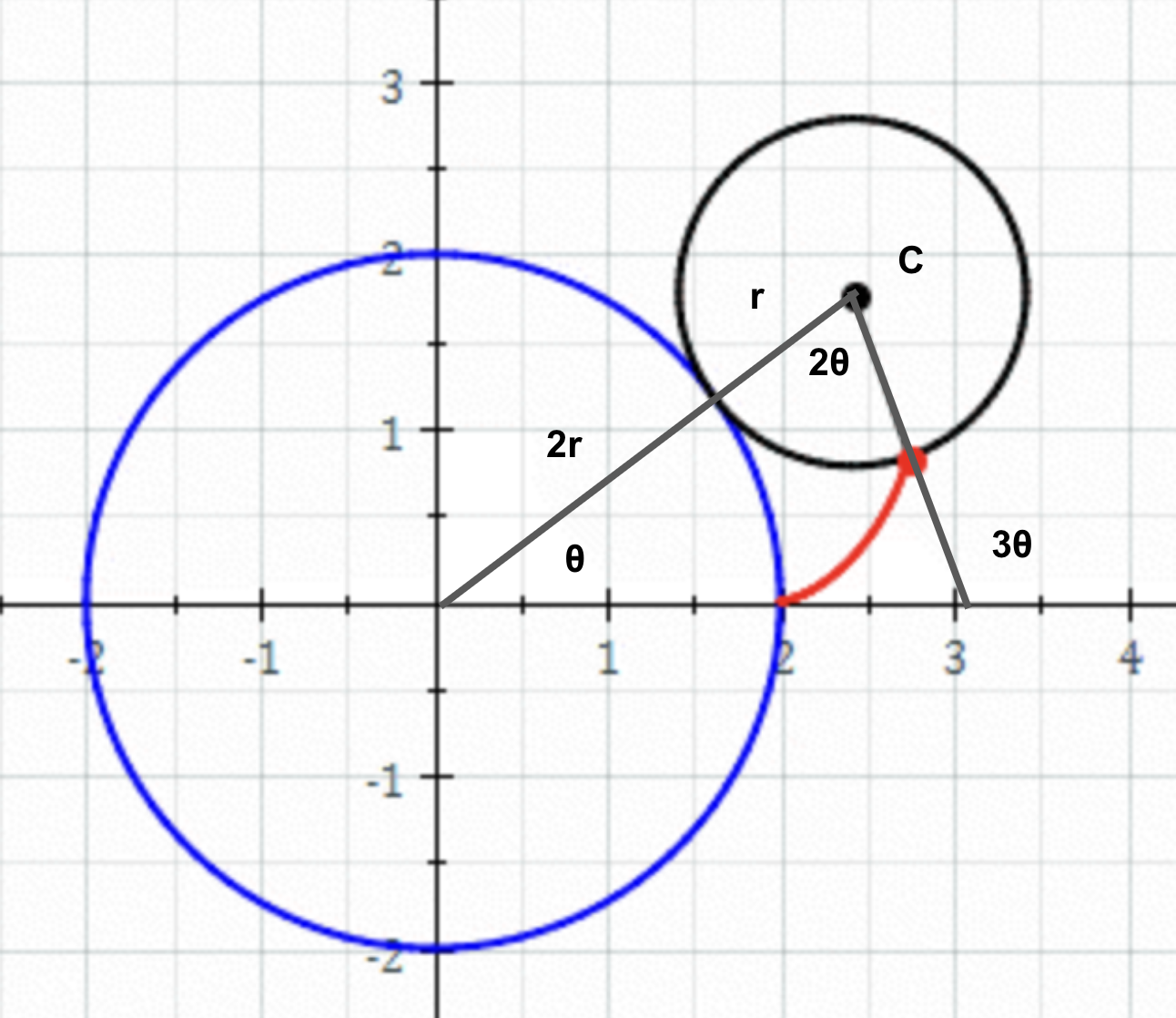
Strophoid

By Kmhkmh - Own work, CC BY 4.0, Link

평면 상에서 곡선 $C$와 고정점 $A$, 그리고 원점 $O$에 의해 생성되는 곡선을 말한다. 만드는 과정은 아래와 같다.

원점 $O$에서 출발해 곡선 $C$를 지나는 직선 $L$을 생각해보자. 직선 $L$이 곡선 $C$와 $K$라는 점을 지나간다. 고정점 $A$와 점 $K$ 사이 거리를 $\overline{AK}$를 반지름으로 하고 점 $K$를 중심으로 하는 원을 하나 생각해보자. 그 원과 직전 $L$이 점하는 두 지점이 있는데, 그걸 $P_1$과 $P_2$라고 하자. 그럼 아래 등식이 성립한다.

\[\overline{AK} = \overline{KP_1} = \overline{KP_2}\]

직전 $L$을 회전화면 이런 조건을 만족하는 점 $P_1$과 점 $P_2$의 자취가 생긴다. 이것을 “Strophoid”라고 한다.

곡선 $C$가 선(line)이라면, 두 개의 Strophoid 곡선은 만들어진다. 이때, 곡선 하나는 고정점 $A$가 위에 존재하는데, 이를 “oblique strophoid”라고 한다.

The nephroid of Freeth

Freeth(1819 - 1904)라는 영국의 수학자가 연구한 곡선이다. 앞에서 Nephroid라는 이름이 붙어있지만, 모양은 다르게 생겼다.

By Robert FERREOL at the mathcurve.com

고정된 원 위의 고정된 한 점 $A$와 원점 $O$를 지나는 직선 $L$이 있다고 하자. 그 직선 $L$이 고정 원을 지나는 점을 $M_0$라고 할 때, 교차점 $M_0$을 원점으로 하고, $\overline{AM_0}$를 반지름으로 하는 원을 떠올려보자. 이때, 그 원과 직선 $L$이 만나는 지점을 $M$, $M’$라고 하자. 그러면 The nephroid of Freeth는 그 두 점 $M$, $M’$이 만드는 자취이다.

극방정식으로 표현하면 아래와 같다.

\[r = 1 + 2 \sin \frac{\theta}{2}\]

$(0, 2\pi)$ 구간에서는 원 바깥의 곡선을 만들고, $(2\pi, 4\pi)$ 구간에서는 원 안의 곡선이 만들어진다.

맺음말

아니 이름 붙은 곡선이 세상에 이렇게나 많은 건지…;; 교재 연습 문제에 나왔던 곡선들을 찾아다 점점 아스트랄 해지는 경험이었다… 🌌

그래도 이젠 굴러다니는 원으로 만들어진 곡선들 같은 거는 확실히 식을 유도할 수 있을 것 같다 ㅋㅋㅋㅋ