Arc Length와 Line Integral
복수전공하고 있는 수학과의 졸업시험을 위해 학부 수학 과목들을 다시 공부하고 있습니다. 미적분학 포스트 전체 보기
드디어 미적분학 교재의 마지막 챕터인 “Integrals and Vector Field”를 공부하고 있다. 미적2를 어렵다고 느끼게 했던 원흉인데, 이번에 다시 공부할 때도 날 괴롭히고 있다… 😈 처음에 “선적분(line integral)”라는 개념에 대해 다루는데, 여기에서부터 헷갈리기 시작해버린… 결국 마음을 다 잡고 개념들을 정리해보기로 마음 먹었다. 곰곰히 생각해보니 선적분이 Arc Length 계산하는 거랑 비슷한 것 같아서 둘을 같이 한번 살펴보겠다.
Arc Length
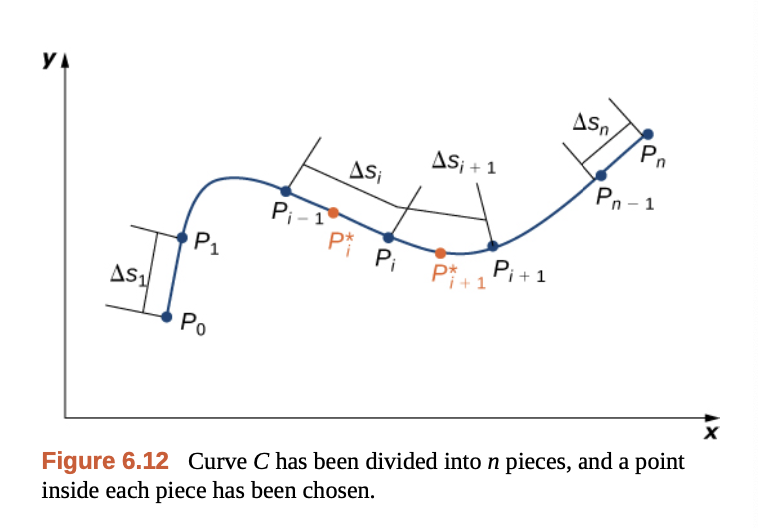Gilbert Strang - Calculus Vol 3.
곡선의 미소변화량 $ds$는 아래와 같이 유도된다.
\[ds = \sqrt{(dx)^2 + (dy)^2 + (dz)^2}\]Arc Length는 결국 미소변화량 $ds$를 적분하는 것과 같다.
Parametrized Curve
xy 평면 위의 곡선 $C$가 $x = f(t)$, $y = g(t)$로 매개화 되어 있다고 하자. 그러면 곡선의 길이는 아래와 같이 계산할 수 있다.
\[L = \int_a^{b} \sqrt{(f'(t))^2 + (g'(t))^2} \, dt\]또는 표기에 따라 곡선이 $(x(t), y(t))$로 매개화 되었다고 하고 아래와 같이 적기도 한다.
\[L = \int_a^{b} \sqrt{(x'(t))^2 + (y'(t))^2} \, dt\]Explicit Function
xy 평면 상에 함수 $y = f(x)$가 그리는 곡선 $C$가 있다고 하자. 이때, 곡선의 길이는 아래와 같이 계산할 수 있다.
\[L = \int_a^{b} \sqrt{1 + (f'(x))^2} \, dx\]Line Integral of a Scalar Field
xy 평면 위에 $(x(t), y(t))$로 그려지는 곡선 $C$가 있다고 하자. 그리고 어떤 이변수 함수 $f(x, y)$를 생각해보자. 요 이변수 함수를 곡선 $C$ 위에서의 선적분을 하면 아래와 같다.
\[\int_C f(x, y) \, ds = \int_{a}^{b} f(x(t), y(t)) \cdot \sqrt{(x'(t))^2 + (y'(t))^2} \, dt\]위에서 봤던 Arc Length와 선적분을 연관해서 본다면, Arc Length는 “$f(x, y) = 1$인 선적분“이라고 볼 수 있다. 즉, 모든 xy 평면 상에서 같은 값을 갖는 함수에 대한 선적분이다.
만약 함수 $f(x, y)$가 xy 평면 상에서의 밀도 함수 $\rho(x, y)$ 였다면, 곡선 $C$에 대한 선적분은 곡선 $C$의 “무게“가 될 것이다.
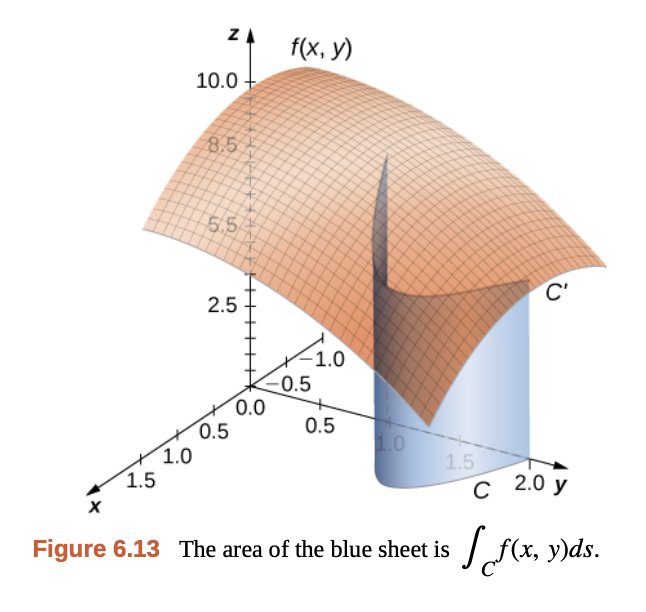Gilbert Strang - Calculus Vol 3.
만약 함수 $f(x, y)$를 z축 상의 어떤 점이라고 본다면, Line Integral은 “곡선이 그리는 벽(fence)의 면적“을 계산하게 된다.
내가 헷갈렸던 점은 이변수 함수 $f(x, y)$와 곡선 $C$가 뭔가 연관이 있을 거라고 생각한 것 같다. 사실 둘은 완전히 독립적인 존재로 곡선 $C$는 그저 적분 구간을 정의하는 것에 불과하다. 그마저도 계산 과정에서는 매개변수 $t$로 표현되어 버리지만…!
표기에 따라서 곡선 $C$를 위치벡터 $\vec{r}(t)$로 표현한다면, Line Integral의 적분식은 아래와 같이 표현된다.
갑자기 등장한 벡터 $\vec{v}(t)$는 속도 벡터로 위치 벡터 $\vec{r}(t)$를 미분한 벡터이다. Line Integral의 공식에서 미소 변위 $ds$가 $| \vec{v}(t) | \cdot dt$로 표현되는게 당연한 듯이 보인다 ㅎㅎ
Line Integral along axis
이번에는 Line Integral을 수행하되, 이걸 선분의 미소변화량 $ds$에 대해서가 아니라 $x$축/$y$축에 대한 미소변화량 $dx$와 $dy$에 대해서 선적분하면 어떻게 되는지 살펴보자. 식으로 표현하면 아래와 같은 식을 살펴보는 것이다.
\[\int_C f(x, y) \, dx = \int_a^{b} f(\vec{r}(t)) \cdot x'(t) \, dt\]Arc Length와 선적분 개념이 익숙해져서 저걸 어떻게 받아드려야 할지 고민이었는데, stackexchange에서 아래와 같은 답변을 찾았다.
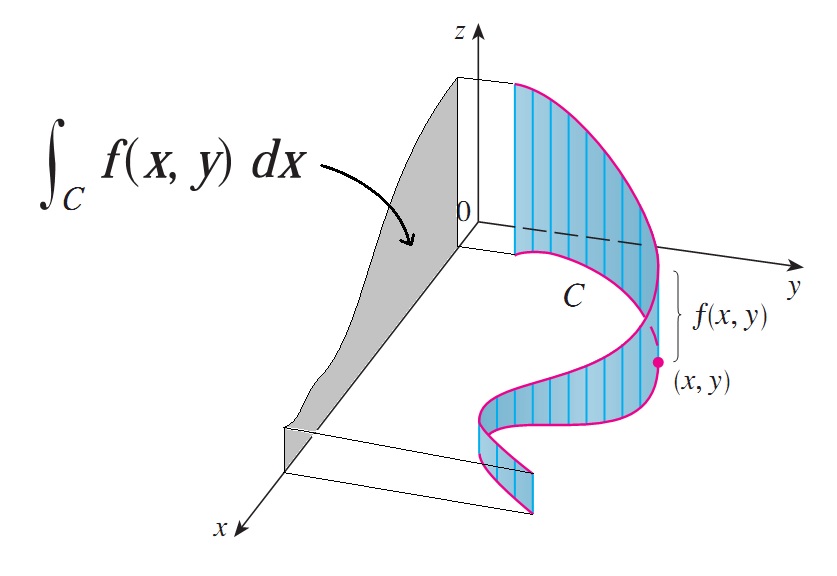
Picture from bfhaha’s answer on math.stackexchange.com
즉, 벽면(fence)을 $x$축 위로 사영하여 만들어지는 영역의 넓이가 바로 $x$축 위로 수행한 선적분 값이다.
Opposite Orientation
선적분에서 적분 커브를 $C$로 표현한다. 만약 커브 $C$가 시점 $A$에서 종점 $B$로 움직이는 경로 커브라면, 앞에 마이너스를 붙인 $-C$ 커브는 종점 $B$에서 시작해 시점 $A$에서 끝나는 반대 경로로 움직이는 커브를 말한다.
위에서 살펴본 Line Integral along axis는 반대 방향 $-C$로 선적분을 수행하면, 적분의 부호가 바뀐다.
\[\int_{-C} f(x, y) \, dx = - \int_C f(x, y) \, dx\]그런데, 그냥 선적분은 반대 경로 $-C$로 적분 하더라도, 부호가 바뀌지 않는다. 이는 선분의 길이를 구하던 Arc Length도 순방향 경로든 역방향 경로든 움직인 거리는 똑같다는 것과 비슷하다. 그리고 애초에 경로의 미소변화량 $ds$는 항상 양의 값을 갖는다.
\[\int_{-C} f(x, y) \, ds = \int_{C} f(x, y) \, ds\]단, 이 성질은 $z = f(x, y)$인 스칼라 함수를 선적분 할 때만 만족한다는 것이다. 벡터 필드를 선적분 할 때는 위의 성질을 만족하지 않는다. 자세한 내용은 후술.
Line Integral of a Vector Field
이변수 함수 $\mathbf{F}(x, y)$가 $\mathbb{R}^2 \rightarrow \mathbb{R}^2$하는 벡터 필드라고 할 때, 이런 벡터 필드에 대한 선적분도 정의할 수 있다. 참고로 적분 결과 역시 스칼라 함수를 적분할 때처럼 스칼라 값으로 나온다.
벡터장에서의 선적분 값은 “일(Work)의 크기“로 해석한다. 물체를 시점 $A$에서 종점 $B$로 옮기면서 드는 일의 크기로 보는 것. 이때, 힘을 받는 벡터장 $\mathbf{F}$과 움직이는 방향 $\mathbf{T}$ 사이에서 일의 미소변화량을 구하면 아래와 같다.
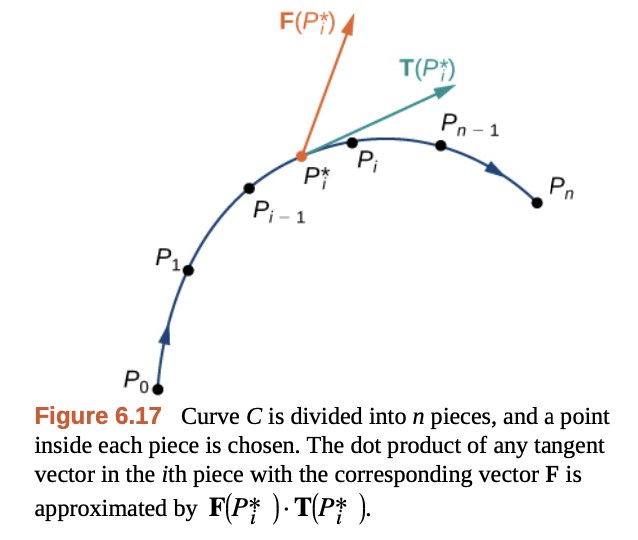Gilbert Strang - Calculus Vol 3.
이를 전체 곡선 $C$에 대해서 정리해서 보면 아래와 같은 적분이 된다.
\[W = \int_C \mathbf{F} \cdot \mathbf{T} \, ds\]위의 적분은 곡선 $C$를 따라 수행된 전체 일의 크기를 계산한 값이다.
이제, 곡선 $C$를 매개변수료 표현해 $\mathbf{r}(t)$로 표기하면, 식은 아래와 같이 바뀐다.
\[W = \int_C \mathbf{F} \cdot \mathbf{T} \, ds = \int_a^b \mathbf{F}(\mathbf{r}(t)) \cdot \frac{d\mathbf{r}}{dt} dt\]또, 벡터 필드 $\mathbf{F}(x, y, z)$의 성분별로 표현하기도 한다.
\[\begin{aligned} & \int_{a}^{b} \left( \mathbf{F}_1 x'(t) + \mathbf{F}_2 y'(t) + \mathbf{F}_3 z'(t) \right) \, dt \\ &= \int_C \mathbf{F}_1 dx + \mathbf{F}_2 dy + \mathbf{F}_3 dz \end{aligned}\]벡터 필드를 선적분 할 때는 Opposite Direction으로 적분하면 아래의 식이 만족한다.
\[\int_{-C} \mathbf{F} \cdot d\mathbf{r} = - \int_{C} \mathbf{F} \cdot d\mathbf{r}\]스칼라 선적분과 달리 부호가 바뀌는 이유는 반대 경로에서는 Tangent Vector $\mathbf{T}$의 방향이 바뀌기 때문이다.
Fundamental Theorem for Line Integrals
요기서부터는 본편인 “Vector Field” 포스트에서 살펴보자 ㅎㅎ