Vector and Space: Problem Solving
복수전공하고 있는 수학과의 졸업시험을 위해 학부 수학 과목들을 다시 공부하고 있습니다. 미적분학 포스트 전체 보기
직선 정의하기
2차원에서
평면 상의 두 점 $(x_1, y_1)$, $(x_2, y_2)$에 대해 두 점을 지나는 직선은 아래와 같이 정의된다.
\[y = \frac{y_2 - y_1}{x_2 - x_1} (x - x_1) + y_1\]3차원에서
공간 상의 두 점 $(x_1, y_1, z_1)$, $(x_2, y_2, z_2)$에 대해 두 점을 지나는 직선은 아래와 같이 정의된다.
\[\frac{x-x_1}{x_2 - x_1} = \frac{y-y_1}{y_2 - y_1} = \frac{z-z_1}{z_2 - z_1}\]다시 하려고 보니 기억이 안 났었다 ㅋㅋㅋ ㅠㅠ 고등학교 때 배웠던 건데…
평면 정의하기
평면을 정의하는 방법은 여러 가지가 있지만, 여기서는 법선 벡터(normal vector) $\vec{n} = (a, b, c)$와 한 점 $(x_0, y_0, z_0)$를 지나는 평면으로 구해보겠다.
\[a (x - x_0) + b(y-y_0) + c(z-z_0) = 0\]내적을 사용해서도 표현할 수 있는데, 한 점 $(x_0, y_0, z_0)$를 시점으로 갖는 벡터 $\vec{p} = (x - x_0, y - y, z-z_0)$를 생각해보자. 그러면 평면은 아래와 같이 내적으로 정의된다.
\[\vec{n} \cdot \vec{p} = 0\]Determine a plane - 1
위의 방정식이 서로 한 직선에 있지 않는(non-collinear), 세 점 $P_1(x_1, y_1, z_1)$, $P_2(x_2, y_2, z_2)$, $P_3(x_3, y_3, z_3)$을 지나는 평면을 정의하는 방정식임을 보여라.
세 점이 구성하는 평면 위에 존재하는 다른 한 점 $P(x, y, z)$를 생각해보자. 그리고 $P$를 종점으로 하는 세 벡터를 생각해보자: $\overrightarrow{P_1P}$, $\overrightarrow{P_2P}$, $\overrightarrow{P_3P}$
이때, $\overrightarrow{P_2P}$, $\overrightarrow{P_3P}$를 외적하여 평면의 법선 벡터 $\vec{n}$을 유도하면 아래와 같다.
\[\begin{aligned} \vec{n} &= (x_2 - x, y_2 - y, z_2 - z) \times (x_3 - x, y_3 - y, z_3 - z) \\ &= \left\| \begin{matrix} i & j & k \\ x_2 - x & y_2 - y & z_2 - z \\ x_3 - x & y_3 - y & z_3 - z \\ \end{matrix}\right\| \end{aligned}\]벡터 $\vec{n}$은 평면의 법선 벡터이므로 $\overrightarrow{P_1P}$와 내적해서 평면의 방정식을 구할 수 있다!! 이때, 내적은 저 행렬식에서 맨 위의 $(i, j, k)$ 부분과 term-by-term으로 수행하면 된다. 따라서
\[\begin{aligned} &(x_1 - x, y_1 - y, z_1 - z) \cdot \left\| \begin{matrix} i & j & k \\ x_2 - x & y_2 - y & z_2 - z \\ x_3 - x & y_3 - y & z_3 - z \\ \end{matrix}\right\| \\ &= \left\| \begin{matrix} x_1 - x & y_1 - y & z_1 - z \\ x_2 - x & y_2 - y & z_2 - z \\ x_3 - x & y_3 - y & z_3 - z \\ \end{matrix} \right\| = 0 \end{aligned}\]$\blacksquare$
Determine a plane - 2
이번에는 아래의 행렬식이 세 점을 지나는 평면을 이룸을 증명해보자.
\[\left\| \begin{matrix} x & y & z & 1 \\ x_1 & y_1 & z_1 & 1 \\ x_2 & y_2 & z_2 & 1 \\ x_3 & y_3 & z_3 & 1 \\ \end{matrix} \right\| = 0\]가우스 소거법? 이었나 그거 비스무리하게 쓰면 된다. 첫 행 $(x, y, z, 1)$을 행렬 전체에 대해 소거 시켜 준다.
\[\left\| \begin{matrix} x & y & z & 1 \\ x_1 - x & y_1 - y & z_1 - z & 0 \\ x_2 - x & y_2 - y & z_2 - z & 0 \\ x_3 - x & y_3 - y & z_3 - z & 0 \\ \end{matrix} \right\| = 0\]이때, 요 4차원 행렬에 대해 행렬식을 구하면 되는데, 신발끈 공식을 써서 진행한다고 해보자. 그런데, 제일 우측의 영벡터인 열벡터 때문데 첫 행의 $x$, $y$, $z$에 곱해지는 $\det A$의 값이 0이 된다. 하지만, 마지막의 $1$에 대한 $\det A$를 구할 때는 0으로 소거되는 부분이 없고, 또한 $\det A$가 바로 위에서 구한 평면을 결정하는 3차원 행렬의 Determinant다!! 즉, 위의 4차원 행렬에 대한 방정식도 3차원에서 세 점을 지나는 평면을 표현하는 방정식이다. $\blacksquare$
Vector Function and Space Curve
함숫값이 벡터인 함수를 말함.
\[\vec{r} (t) = \left( f(t), g(t), h(t) \right)\]연속인 벡터 함수는 공간 상에서 곡선을 그린다.
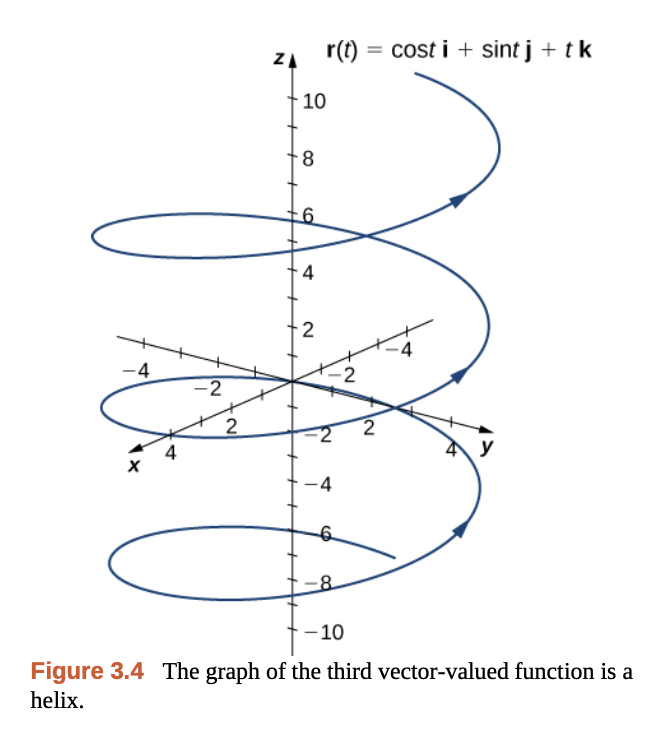Gilbert Strang - Calculus Vol 3.
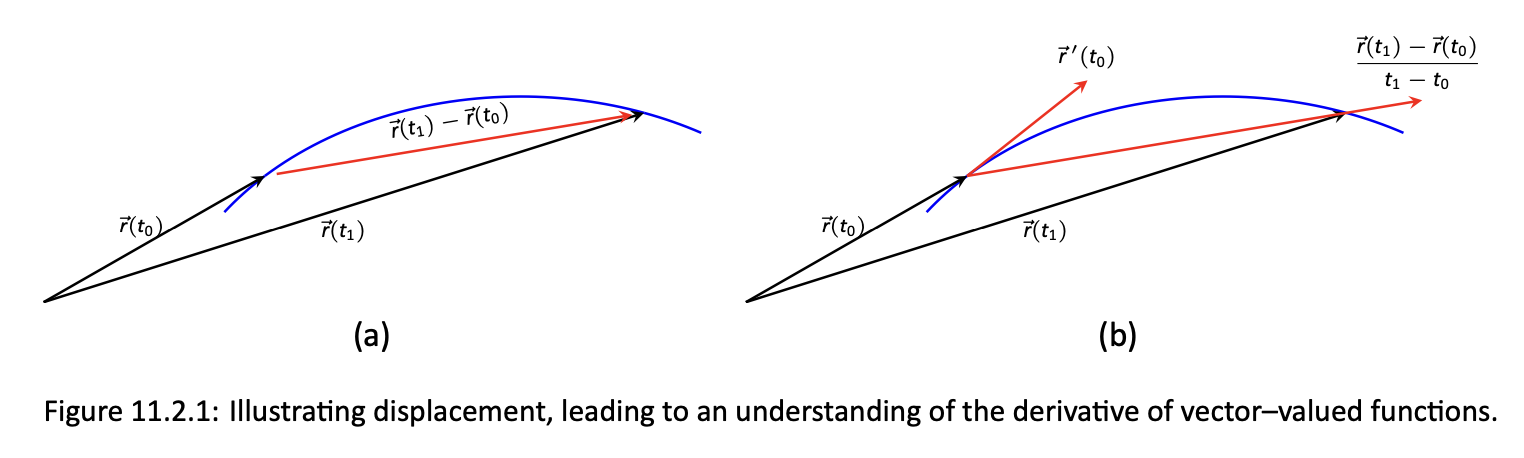
Tangent Vector
벡터 함수 $\vec{r}(t)$를 term-by-term으로 미분한 함수를 말한다.
\[\vec{r}'(t) = \left( f'(t), g'(t), h'(t) \right)\]공간 곡선의 한 점에 접하는 직선의 방향이라고 볼 수 있다. Tangent Vector의 방향만 알고 싶을 때는 Unit Tangent Vector를 사용한다.
\[\vec{T}(t) = \frac{\vec{r}'(t)}{\left| \vec{r}'(t) \right|}\]Vector Functions of Constant Length
벡터 함수 $\vec{r}(t)$의 길이가 상수값 $c$로 고정 되어 있다면, 아래 등식이 성립한다.
\[\vec{r}(t) \cdot \vec{r'}(t) = 0\]즉, 벡터 함수의 그것의 접선 벡터가 서로 수직이다.
예를 들어, 2차원의 원 위에서 한 점에서 그은 Tangent Vector는 항상 위치 벡터 $\vec{r}(t)$와 수직한다. 이것은 3차원 이상에서도 성립한다.
증명은 어렵지 않다.
$\blacksquare$
Normal Vector
Unit Tangent Vector $\vec{T}(t)$에 대해 수직하는 법선 벡터(Normal Vector)를 찾고자 한다. 그런데 유일하게 결정되는 Unit Tangent Vector와 달리 $\vec{T}(t)$에 수직하는 법선 벡터는 무수히 많다…!
이때, 접선 벡터 $\vec{T}(t)$가 길이 1인 unit vector이므로 아래의 등식이 성립한다.
\[\vec{T}(t) \cdot \vec{T}'(t) = 0\]즉, 접선 벡터 $\vec{T}(t)$를 또 하나의 공간 곡선으로 보고, 그것의 접선 벡터 $\vec{T}’(t)$를 구해보면, 그 둘이 수직 관계에 있다는 것이다…!
이 사실을 바탕으로 아래와 같은 법선 벡터를 정의해보자.
\[\vec{N}(t) = \frac{\vec{T}'(t)}{\left| \vec{T}'(t) \right|}\]접선 벡터의 접선 벡터로 정의한 요 법선 벡터를 “Principal Unit Normal Vecor” $\vec{N}(t)$라고 부른다. 편하게 “unit normal”라고도 부른다.
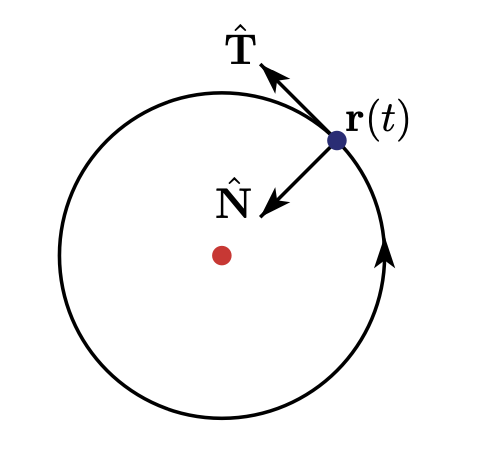
Normal Vector는 항상 곡선의 안쪽 방향(inner side of the curve)을 가리킨다는 특징이 있다. 예를 들어, 위의 그림처럼 법선 벡터가 곡선의 안쪽을 항할 수 있지만, 곡선의 바깥쪽으로 향해도 접선 벡터 $\vec{T}(t)$와 수직한다. 서로 반대 방향의 법선 벡터 중에 선택되는 것은 항상 안쪽 방향의 벡터다.
외적의 방향을 결정할 때 자주 쓰는 오른손 법칙으로 쉽게 생각하면,
- 검지 = 접선 벡터 $\vec{T}(t)$
- 엄지 = 법선 벡터 $\vec{N}(t)$
- 중지 = 종법선 벡터 $\vec{B}(t)$ (xy 평면에서는 z축 방향을 가리킴)
Binormal Vector
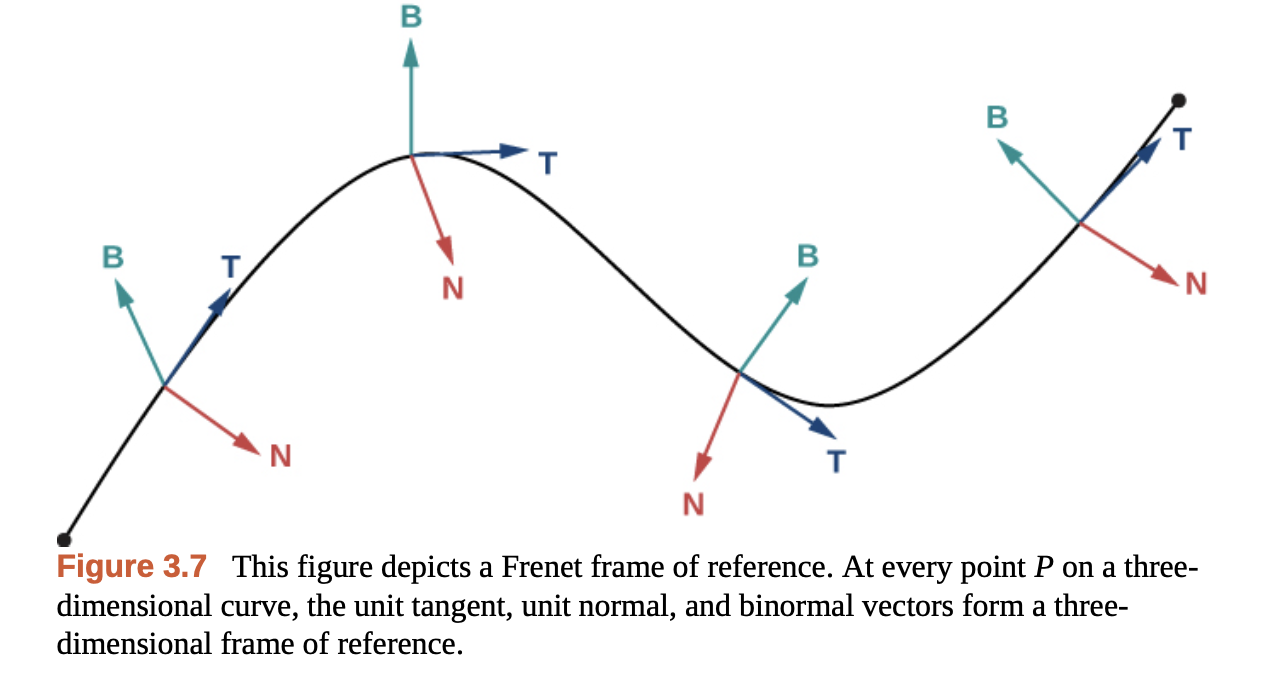Gilbert Strang - Calculus Vol 3.
서로 수직하는 두 벡터를 “외적”하면, 그 두 벡터에 수직하는 또 다른 벡터를 얻을 수 있다는 사실을 기억하는가!! 앞에서 서로 수직하는 두 벡터 $\vec{T}(t)$, $\vec{N}(t)$를 구했으니, 외적을 이용해 또 다른 수직 벡터를 구할 수 있다!!
\[\vec{B}(t) = \vec{T}(t) \times \vec{N}(t)\]접선 벡터와 법선 벡터의 외적으로 유도되는 이 벡터를 “종법선 벡터(Binormal Vector)“라고 부른다. 아마 두 벡터에 둘(bi-) 다 수직(normal)인 관계를 만족해서 “Binormal”라는 이름이 붙은게 아닐까…?
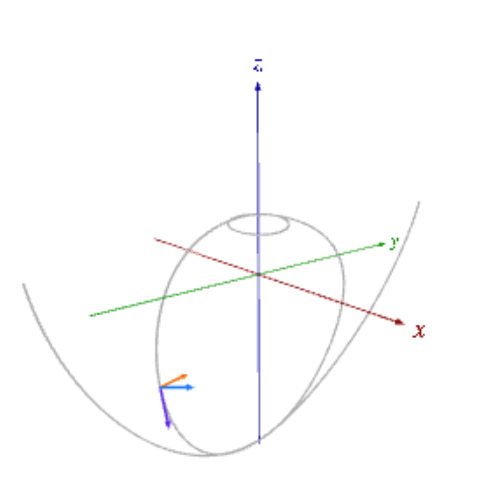
The TNB Frame
공간 곡선의 한 점에서 유도되는 서로 직교하는 세 벡터 $\vec{T}$, $\vec{N}$, $\vec{B}$를 하나의 좌표계로 해석하는 것을 말한다. xyz 좌표계와 별개로써 공간 곡선 위를 한 점이 이동하면서 곡선의 곡률(curvature), 열률(torsion)에 따라 시시각각 좌표계가 변화하게 되는데, 이를 잘 표현해준다.
stewartcalculus.com에서 에니메이션과 함께 TNB 좌표계를 더 잘 이해해볼 수 있다.
어렸을 때 정말 많이 했던 롤코2... ㅋㅋ
어떻게 보면 “롤러코스터“를 탈 때, 레일 위의 시시각각 변하는 열차의 좌표계라고 이해하면 쉬운 것 같다.
Many shapes on 3-dim space
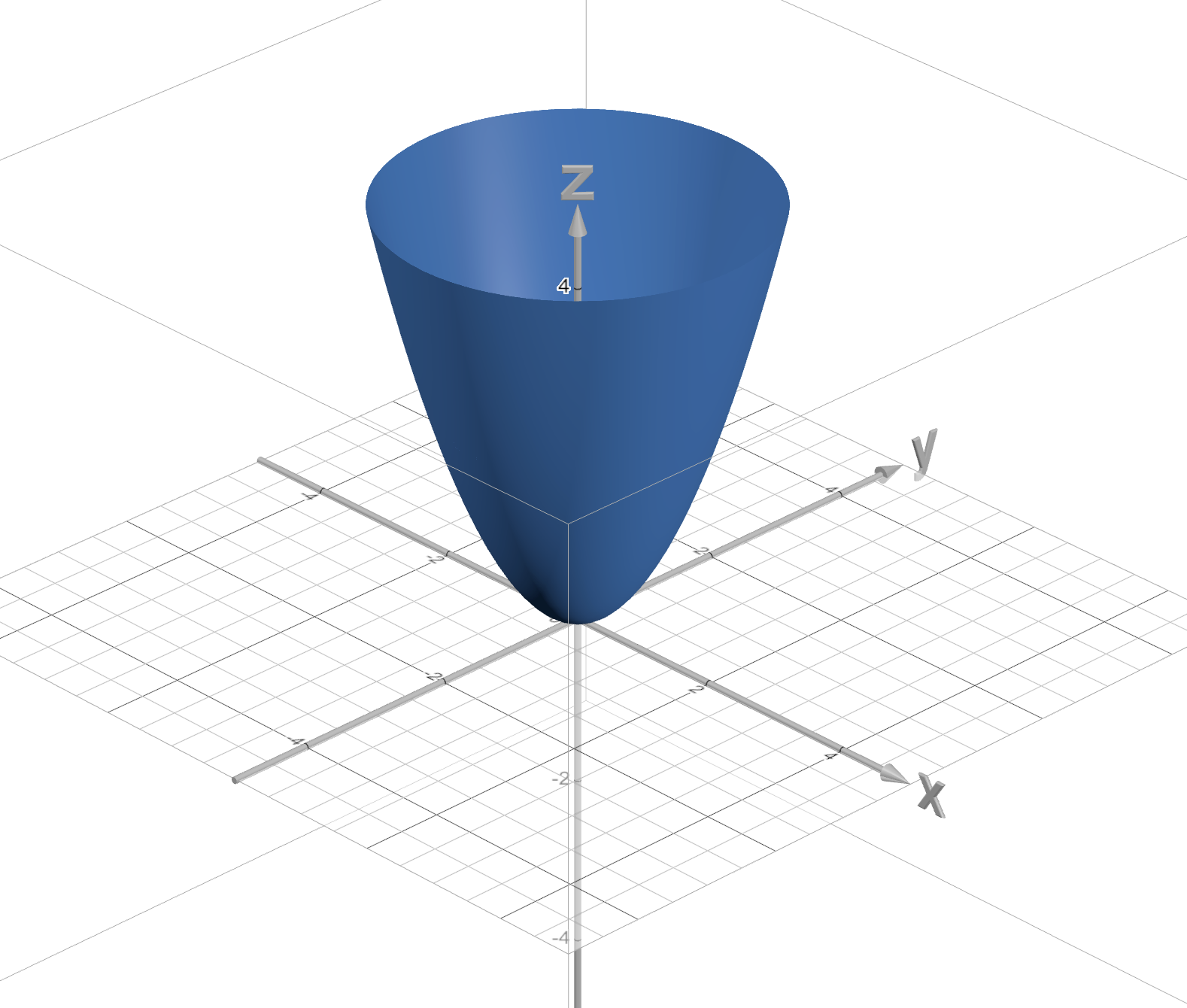
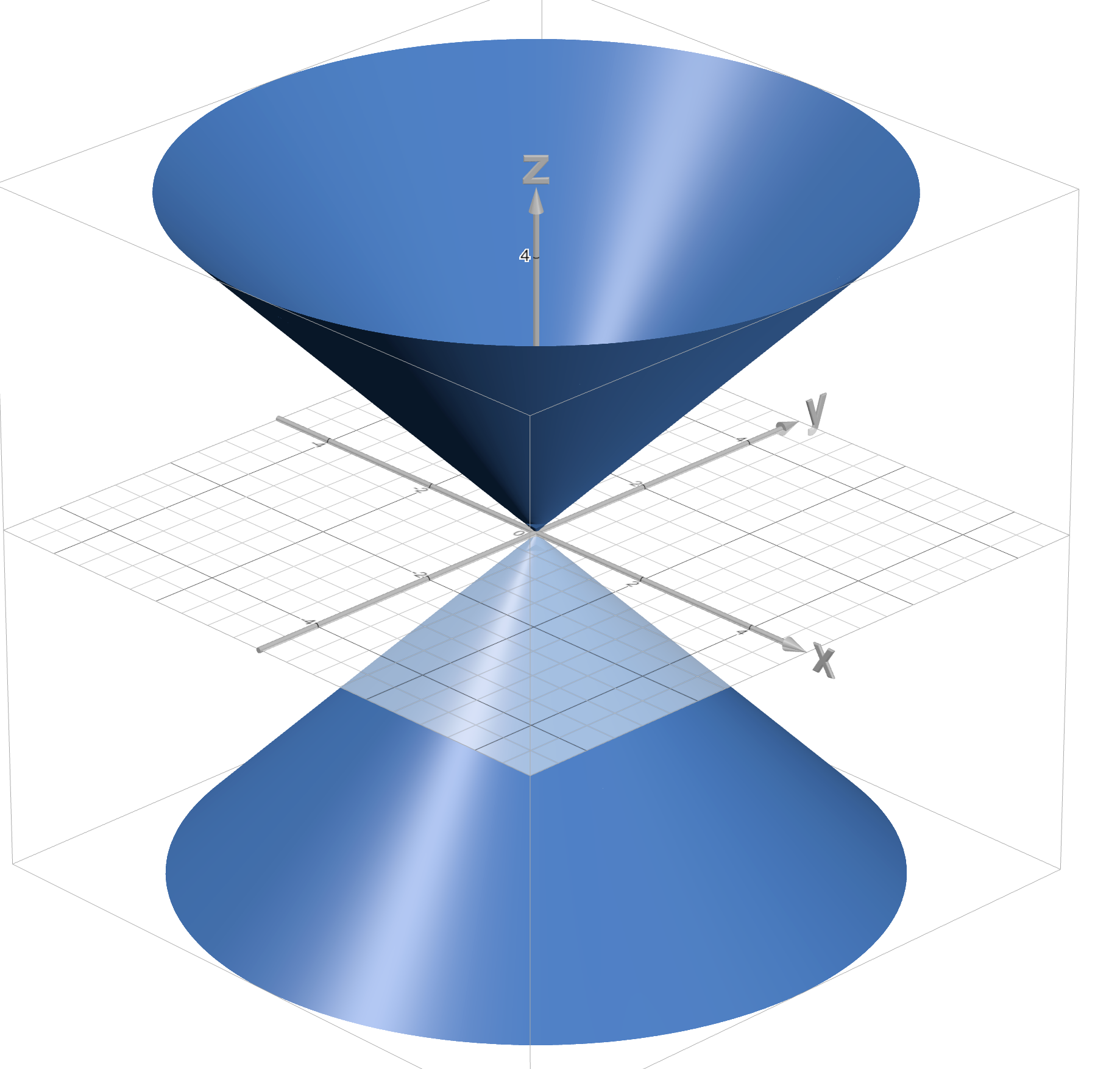
맺음말
뭔가 미분기하(Differential Geometry)의 입문적인 파트라고 하는데… 뭔가 3차원 공간 위에서 이리저리 움직이고 또 모형을 상상해봐야 해서 머리가 아픈 것 같다… ㅠㅠ 이때까지는 머리속에서 생각만 슥슥 했으면 됐는데 ㅠㅠ