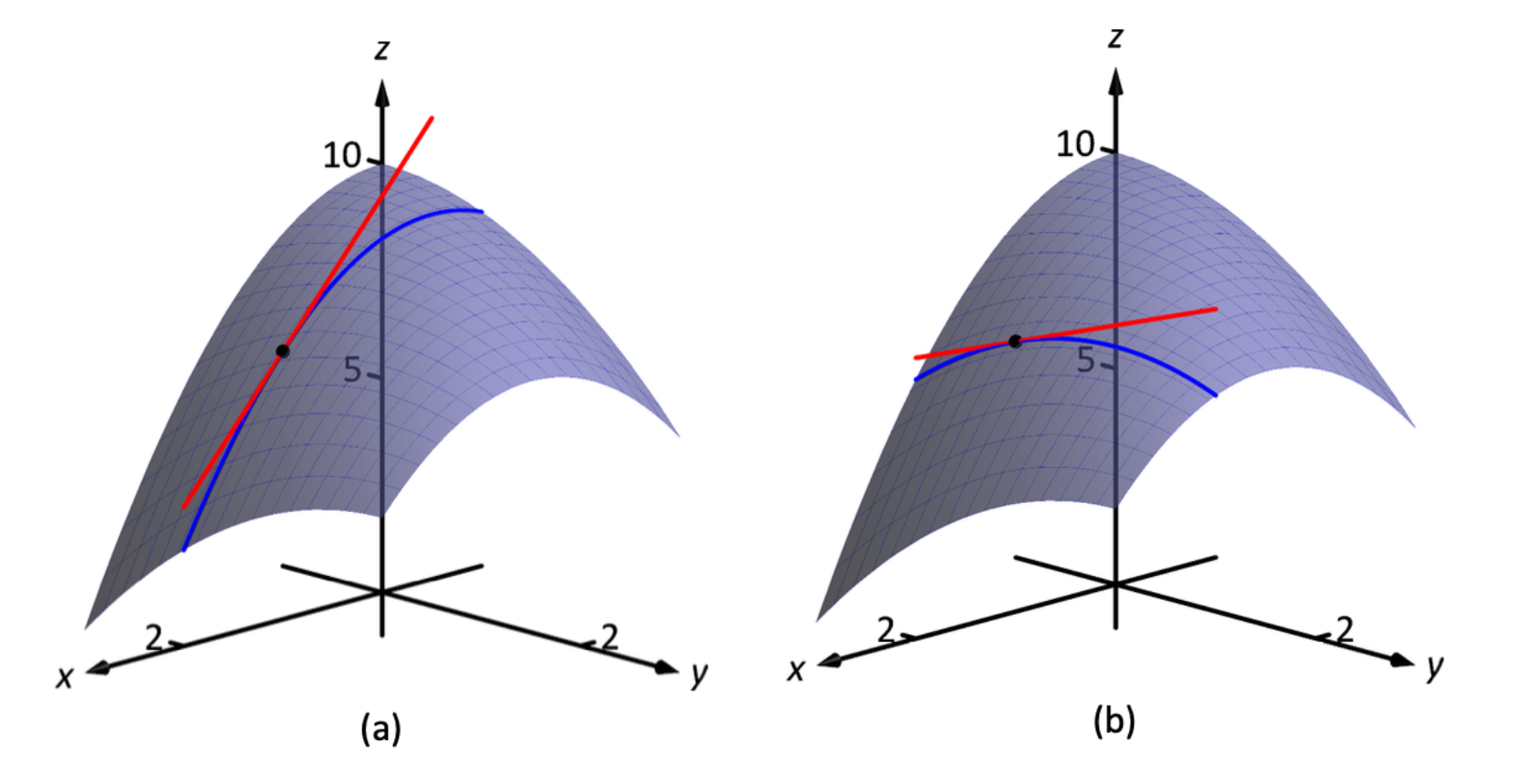
Partial Derivatives and Differentiability
복수전공하고 있는 수학과의 졸업시험을 위해 학부 수학 과목들을 다시 공부하고 있습니다. 미적분학 포스트 전체 보기

이번 챕터는 개념들이 너무너무 헷갈려서 문제 풀이보다는 교재의 개념들을 제대로 이해하는 것에 초점을 두었다. 😵💫
Limit of 2-dimensional function
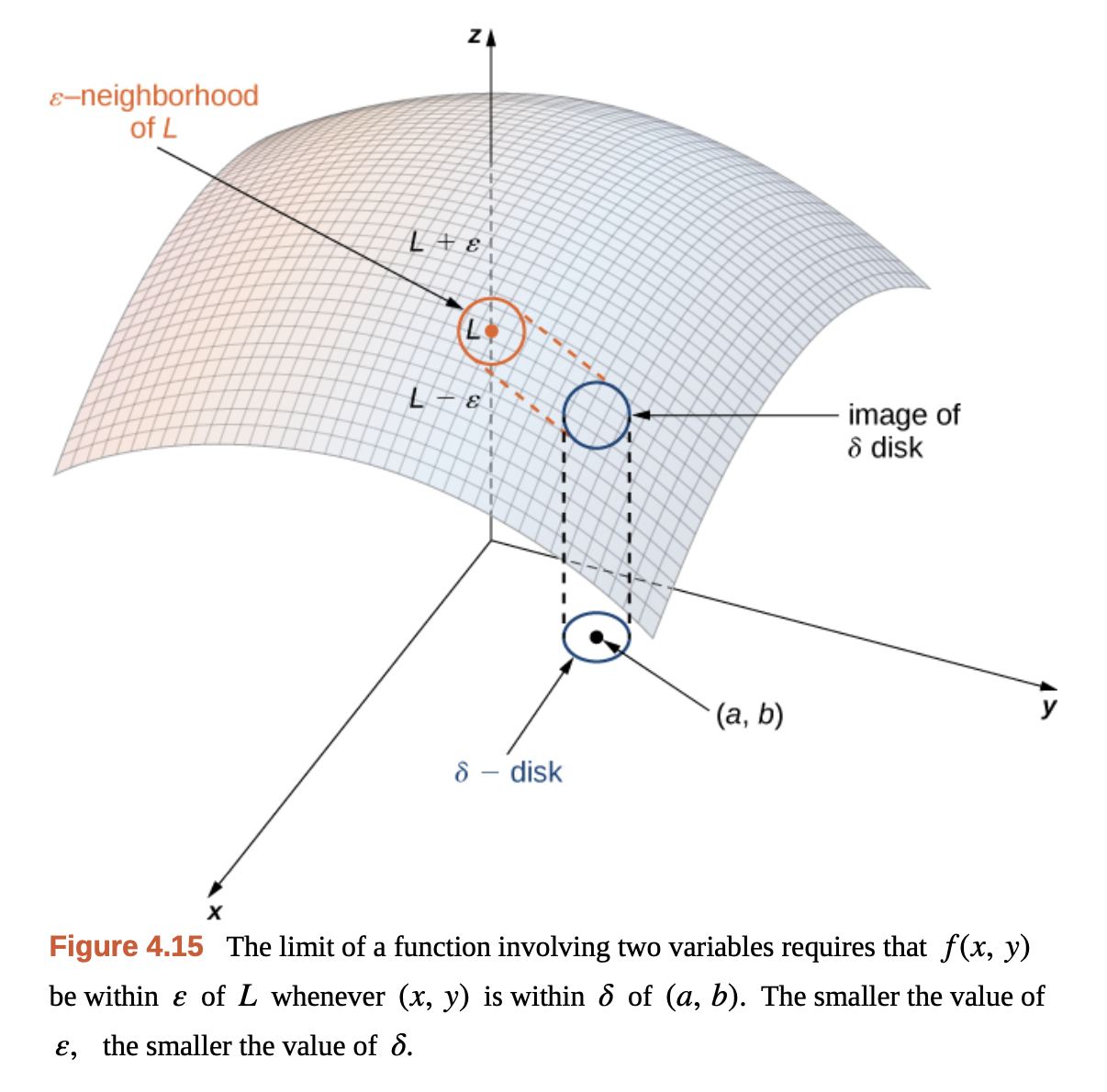
A function $f(x, y)$ approaches the limit $L$ as $(x, y)$ approaches $(x_0, y_0)$
\[\lim_{(x, y) \rightarrow (x_0, y_0)} f(x, y) = L\]if for every $\epsilon > 0$, there exists a corresponding $\delta > 0$ s.t. for all $(x, y)$ in the domain of $f$,
$|f(x, y) - L| < \epsilon$ whenever $0 < \sqrt{(x-x_0)^2 + (y-y_0)^2} < \delta$.
이변수 함수에서의 극한을 입델 논법으로 정의한 문장이다. 극한값 $L$ 근방의 어떤 값을 잡아도, 그에 대응하는 $\sqrt{(x-x_0)^2 + (y-y_0)^2} < \delta$ 범위를 잡아서, 그 안의 모든 $(x, y)$에 대해 함숫값이 $\epsilon$ 범위 안에 들어가는 $\delta$를 결정할 수 있음으로 이변수 함수의 극한을 정의한다.
 Gilbert Strang - Calculus Vol 3.
Gilbert Strang - Calculus Vol 3.
반대로 $\delta$의 근방(disk)를 잡았을 때, 그 안의 어떤 점의 집합이 $\epsilon$ 범위를 벗어나는 경우가 있다면, 함수의 극한값을 결정할 수 없거나 제시한 극한값이 올바르지 않다고 말할 수 있다.
Examples of the limit non-exsistance
Does $f(x, y) = \frac{y}{x}$ has a limit of $\lim_{(x, y) \rightarrow (0, 0)} f(x, y)$?
일단 함수 $f(x, y)$의 도메인은 분모의 $x$ 때문에 $x \ne 0$인 $\mathbb{R}^2$ 영역 전체이다.
먼저 $x \ne 0$인 $(x, 0)$ 영역 전체를 살펴보자. 그러면, 분자의 값이 0이기 때문에 극한값 $L$은 $L = 0$이 될 수 있다.
그러나 $y = x$인 상황을 생각해보면, $f(x, x) = \frac{x}{x} = 1$이 된다. 즉, 앞에서 $L = 0$인 것과 일치하지 않는다.
이것은 어떤 $\delta$ 범위의 disk를 정의하고, 극한값을 $L = 0$ 또는 $L = 0$ 둘 중 하나로 잡아도 $\epsilon$ 범위를 벗어나게 된다는 것을 말한다.
사실 $y = ax$ 관계를 만족한다면, 극한값은 어떤 실수 $a$가 된다. 어떤 방향으로 $(0, 0)$에 접근해도 극한값이 달라지므로 극한값은 존재하지 않는다.
아래의 함수가 원점 $(0, 0)$에서 연속인지 결정하라.
\[f(x, y) = \begin{cases} \frac{2xy}{x^2 + y^2} & (x, y) \ne (0, 0) \\ 0 & (x, y) = (0, 0) \end{cases}\]원점에 $x$ 축을 따라 접근한다면, $(x, 0)$에 대해서 함숫값은 $0$으로 근접한다.
반대로 $y$ 축을 따라 접근한다면, $(0, y)$에 대해서도 함숫값은 $0$으로 근접한다.
하지만, $y = x$ 직선을 따라 접근한다면, $(x, x)$에 대해서 함숫값은 $1$로 근접한다. 이것은 $y = ax$ 조건을 만족하는 어떤 직선을 따라 접근하더라도 $\frac{2a}{a^2 + 1}$의 값으로 근접한다.
즉, 함숫값이 어떤 하나로 결정되지 않으므로 $(0, 0)$에서 함숫값이 존재하지 않고, 원점에서 “불연속”이다.
Two Path Test for Non-existence of a Limit
함수가 어떤 점에서 극한이 존재하지 않음을 보이는 쉬운 방법으로 아래 방법이 정립되어 있다. $\delta$ 범위의 disk에서 2가지 방향으로 접근했을 때 극한값이 다르다면, 함수는 해당 점에서 극한이 존재하지 않는다고 말할 수 있다.
If a function $f(x, y)$ has different limits along two different paths in the domain of $f$ as $(x, y)$ approaches $(x_0, y_0)$, then $\lim_{(x, y) \rightarrow (x_0, y_0)} f(x, y)$ does not exist.
이때, 주의할 점은 명제의 역은 성립하지 않는다. 만약 2가지 방향으로 접근 했을 때 두 극한값이 같다고 해서 함수가 그 극한값을 가진다고 말할 수 없다!! 이것은 앞에서 살펴본 $f(x, y) = \frac{2xy}{x^2 + y^2}$ 함수 경우에서도 볼 수 있는데, $x$ 축, $y$ 축 방향으로 접근했을 때의 극한값이 둘다 $0$이었지만, $y = ax$ 방향 접근할 때의 극한값이 $0$과 다른 값을 가진다.
Limit on Polar Coordinate
만약 rectangular coordinates에서 원점에 대한 극한 $\lim_{(x, y) \rightarrow (0, 0)} f(x, y)$에 대한 극한을 구하기 어렵다면, polar coordinate를 사용해 극한을 구하는 방법을 고려해볼만 한다. 이 경우, 함수 $f(x, y)$를 $f(r, \theta)$의 형태로 표현하고, $r \rightarrow 0$으로 보내는 방식으로 원점에 대한 극한을 구한다.
Given $\epsilon > 0$, there exists a $\delta > 0$ s.t. for all $r$ and $\theta$,
if $| r | < \delta$, then $| f(r, \theta) - L| < \epsilon$.
If such an $L$ exists, then
\[\lim_{(x, y) \rightarrow (0, )} f(x, y) = \lim_{r \rightarrow 0} f(r\cos \theta, r\sin \theta) = L\]예제와 함께 극좌표를 사용한 극한 계산을 살펴보자.
이것을 확인하려면, $r \cos^3 \theta$의 $r \rightarrow 0$에 대한 극한값 $L$이 0으로 수렴하는지를 체크해야 한다.
Let’s find $\delta > 0$ which satisfies the below statement
IF $| r | < \delta$, then $| r \cos^3 \theta - 0| < \epsilon$ for any given $\epsilon > 0$, and $r$ and $\theta$.
We know the range of $\cos \theta$, the below inequality satisfies
\[\| r \cos^3 \theta - 0\| \le \| r \| < \delta\]If we take $\delta$ as $\delta = \epsilon$, then the statement of limit holds.
극좌표 변환을 통해 극한값이 존재하지 않음도 확인할 수 있다.
이 경우는 $| r |$ 값이 아무리 작더라도 $\cos^2 \theta$에 의해 값이 0부터 1사이 값을 갖게 된다. 즉, 수렴하지 않는다.
그러나 때로는 극좌표 변환으로 구하는 극한이 잘못된 결론을 이끌게 할 수도 있다.
이때, 분자의 $r$ 때문에 $r \rightarrow 0$으로 가면 0으로 수렴한다고 생각할 수 있다. 하지만, 그건 틀렸다!!
만약 극한이 $y = x^2$의 경로로 원점에 접근한다면, $r \sin \theta = r^2 \cos^2 \theta$가 되고, 이것을 대입하면,
\[\begin{aligned} & \frac{2 r \cos^2 \theta \sin \theta}{r^2 \cos^4 \theta + \sin^2 \theta} \\ =& \frac{2 r \cos^2 \theta \cdot r \cos^2 \theta}{r^2 \cos^4 \theta + r^2 \cos^4 \theta} \\ =& \frac{2r^2 \cos^4 \theta}{2 r^2 \cos^4 \theta} \\ =& 1 \end{aligned}\]즉, 원점에서의 극한값은 $1$이 된다.
Differentiability of 2-dimension
Meaning of Partial Derivative
이변수 함수 $f(x, y)$에 대한 편미분 $\partial x$, $\partial y$는 어떤 점에서의 함수에 접하는 접선의 기울기를 의미한다. 구체적으로는 $x$축 방향의 접선의 기울기와, $y$축 방향의 접선의 기울기를 의미한다.
이를 이용해서 함수 $f(x, y)$ 위의 점 $(x_0, y_0)$에 접하는 접평면의 방정식을 유도할 수 있다.
\[z = f(x_0, y_0) + f_x(x_0, y_0) \cdot (x - x_0) + f_y(x_0, y_0) \cdot (y - y_0)\]그리고 이 접평면은 이변수 함수 $f(x, y)$를 “선형 근사”한 식으로 볼 수 있다.
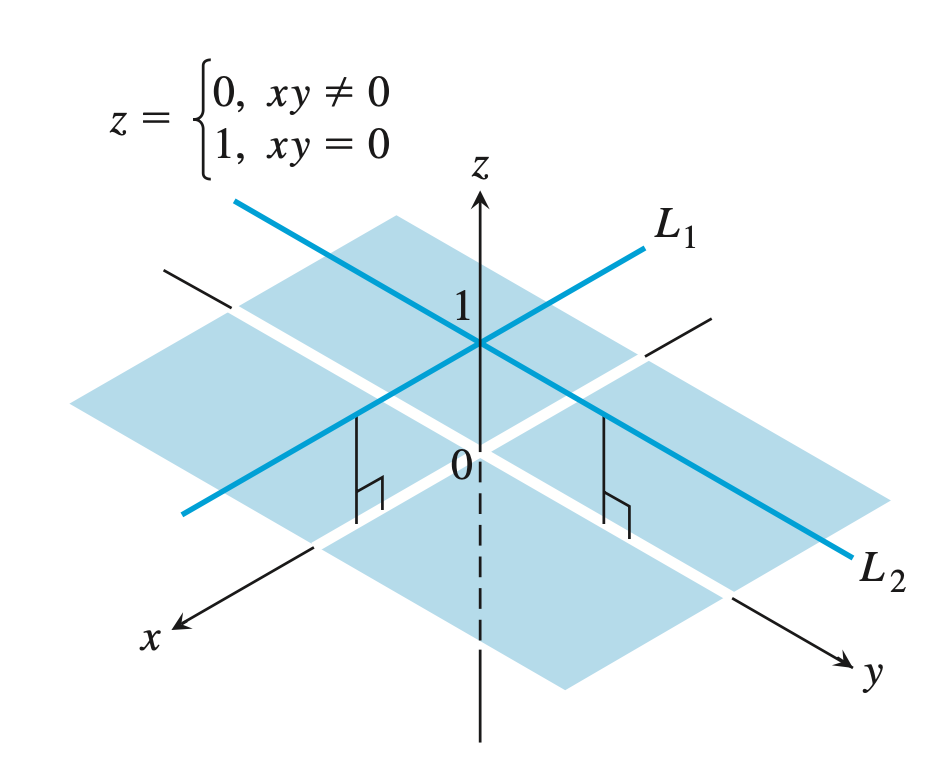
Partial Derivatives exist, but not continuous
\[f(x, y) = \begin{cases} 0, & xy \ne 0 \\ 1, & xy = 0 \end{cases}\]위와 같은 함수를 생각해보자. 이 함수는 $x$축, $y$축과 원점에서는 1의 값을 갖고 나며지 영역에서는 모두 0의 값을 갖는다.
 Thomas Calculus 13th ed. - Example Problem
Thomas Calculus 13th ed. - Example Problem
원점 $O$에서의 함수의 극한을 생각해보자.
(1) 만약 $x$축 또는 $y$축을 따라서 원점에 접근한다면, 극한값은 $1$이 된다.
(2) 하지만 $y = x$ 또는 (1)의 경로를 제외한 다른 방식으로 접근한다면, 극한값은 $0$이 된다.
즉, 원점 $O$에서 함수의 극한은 존재하지 않는다.
반면에 원점에서의 Partial Derivative는 존재한다. 둘다 $x$축, $y$축 위에서 값의 변화가 없으므로 Partial Derivative의 값은 0, 변화없음이다.
\[\frac{\partial f}{\partial x} = \frac{\partial f}{\partial y} = 0\]Differentiability implies Continuity
$y = f(x)$ 꼴의 함수에서도 어떤 점에서의 미분가능성은 해당 점에서의 연속성을 보장했다. 하지만, 위의 예에선 원점에서 편도함수(Partial Derivative)가 존재했지만, 원점에서 연속성은 갖지 못했다. 미분가능성이 연속성을 보장하는 것은 $y = f(x)$ 함수꼴에서만 성립하는 명제인 것인가?
이에 대한 답변은 “다차원(multi-dimension)에서도 미분가능성은 연속성을 보장된다.“라고 말할 수 있다.
위의 예제는 편도함수의 존재 여부는 함수의 미분가능성과 전혀 별개의 속성이라 교훈을 가장 간단한 형태로 말해준다.
The Mixed Derivative Theorem
편미분을 수행하다보면, 무의식적으로 아래의 두 편미분 값이 같은 걸 발견할 수 있다.
\[\frac{\partial^2 f}{\partial y \partial x} = \frac{\partial^2 f}{\partial x \partial y}\]그러나 이것은 우연히도 함수 $f(x, y)$가 아주 나이스한 함수이기 때문이 위의 등식을 만족하는 것이다. 이것에 대해서 정리한 것이 아래의 “Clairaut’s Theorem(클레로의 정리)“이다.
If $f(x, y)$ and its partial derivatives $f_x$, $f_y$, $f_{xy}$, and $f_{yx}$ are defined throughout an open region containing a point $(a, b)$ and are all continuous at $(a, b)$, then
\[f_{xy}(a, b) = f_{yx}(a, b)\]즉, 편미분의 교환법칙이 성립하기 위해선 모든 편미분이 존재하고, 또 해당 지점에서 연속이어야 한다.
Differentiability
함수 $z = f(x, y)$가 점 $(x_0, y_0)$에서 미소량 $\Delta x$, $\Delta y$만큼 움직일 때의 증분 $\Delta z$는 아래의 식으로 정의 해보자.
\[\Delta z = f(x_0 + \Delta x, y_0 + \Delta y) - f(x_0, y_0)\]이때, 함수 $f(x, y)$를 점 $(x_0, y_0)$에서 선형 근사하면 아래와 같다. (이것은 점 $(x_0, y_0)$에서의 접평면과 같다)
\[L(x, y) = f(x_0, y_0) + f_x(x_0, y_0) \cdot (x - x_0) + f_y(x_0, y_0) \cdot (y - y_0)\]이것을 증분 $\Delta z$에 대한 식에 대입하여 $L(x, y)$에 대한 증분 $\Delta L$를 유도하면 아래와 같다.
\[\Delta L = f_x \cdot \Delta x + f_y \cdot \Delta y\]위의 식을 바탕으로 증분 $\Delta z$에 대한 식을 아래와 같이 작성해보자.
\[\Delta z = \Delta L + \epsilon_1 \Delta x + \epsilon_2 \Delta y\]선형 근사는 말 그대로 근사식이다. 따라서 실제 함숫값의 증분인 $\Delta z$와는 차이가 있을 수 밖에 없고, 이것을 $\epsilon_1$, $\epsilon_2$로 정의한 것이다.
위의 식을 통해 함수 $f(x, y)$의 미분가능성(Differentiability)를 아래와 같이 정의한다.
A function $z = f(x, y)$ is differentiable at $(x_0, y_0)$ if
- $f_x(x_0, y_0)$ and $f_y(x_0, y_0)$ exist
- and $\Delta z$ satisfies an equation of the form
in which each $\epsilon_1, \epsilon_2 \rightarrow 0$ as both $\Delta x, \Delta y \rightarrow 0$.
위의 문장을 잘 이해해보면, 점 $(x_0, y_0)$의 근방인 $\Delta x, \Delta y \rightarrow 0$에서 오차값인 $\epsilon_1$와 $\epsilon_2$가 0으로 수렴하여 함수의 증분과 선형 근사의 증분이 같아진다면, 함수 $f(x, y)$가 그 점에서 미분가능하다고 말하는 것이다.
\[\Delta z \approx \Delta L\]만약 함수가 정의역(Domain) 전체에서 미분가능하다면, 그 함수를 differential function라고 부르며, 함수의 그래프가 smooth surface를 갖는다고 말한다.
Continuous Partial Derivatives implies Differentiability
만약 함수의 편미분이 연속이라면, 함수가 해당 점에서 미분 가능하다고 말할 수 있다.
Supp. the first partial derivatives of $f(x, y)$ are defined, and $f_x$ and $f_y$ are “continuous” at $(x_0, y_0)$. Then the function $f(x, y)$ is differential at $(x_0, y_0)$.
앞에서 살펴봤던 함수를 다시 가져와보자.
\[f(x, y) = \begin{cases} \frac{2xy}{x^2 + y^2} & (x, y) \ne (0, 0) \\ 0 & (x, y) = (0, 0) \end{cases}\]이 함수는 편도함수 $f_x$가 존재한다. 하지만, 아래와 같은 형태를 갖는다.
\[f_x(x, y) = \begin{cases} 0 & y = 0\\ 0 & x \ne 0, y \ne 0 \\ \texttt{not exist} & x = 0, y \ne 0 \\ \end{cases}\]이 경우, 편도함수 $f_x$는 원점의 근방에서 극한이 존재하지 않는 지점이 있어 연속성을 갖지 않는다. 따라서 $f(x, y)$는 원점에서 미분불가능하다.
Differentiability implies Continuity
바로 윗 명제의 역 명제를 살펴보자.
If a function $f(x, y)$ is differentiable at $(x_0, y_0)$, then $f$ is continuous at $(x_0, y_0)$
이것은 미분가능의 정의에서 쉽게 유도할 수 있는데, 일단 함수가 미분 가능하다는 것은 증분 $\Delta z$가 선형근사의 증분 $\Delta L$과 같아진다는 걸 의미한다.
\[\Delta z = \Delta L = f_x(x_0, y_0) \cdot (x - x_0) + f_y(x_0, y_0)\]그런데, $\Delta x, \Delta y \rightarrow 0$라면, 선형근사의 증분 $\Delta L$이 0으로 수렴한다. 이것은 $f_x(x_0, y_0)$와 $f_y(x_0, y_0)$의 값이 고정값이기 때문에 $\Delta x, \Delta y \rightarrow 0$라면 덩달아 0에 수렴하기 때문이다.
미분가능성은 $\Delta z = \Delta L$을 보장하므로, $\Delta z$도 0으로 수렴한다. 이것은 함수 $f(x, y)$가 해당 점에서 연속성을 가짐을 말한다.
Total Differential
함수 $f(x, y)$가 한 점에서 미분가능한 경우, 그것의 증분 $\Delta z$를 선형근사식의 증분 $\Delta L$로 표현할 수 있었다. 위와 같은 미분 가능 상황에서 정의한 증분 $\Delta z$를 “전미분(Total Derivative)“라고 하며 $dz$라고 표기한다.
\[dz = f_x \cdot \Delta x + f_y \cdot \Delta y = \Delta L\]연습문제를 하나 풀어보자.
반지름 $r$이 2%씩 증가하고, 높이 $h$가 1%씩 증가하는 원뿔의 부피 변화량을 계산하라.
부피 $V(r, h) = \frac{\pi r^2 h}{3}$의 부피 변화율인 $dV$를 구하는 문제다. Total Derivative를 사용하면, 쉽게 부피 변화량을 계산할 수 있다.
\[\begin{aligned} dV &= V_r \cdot dr + V_h \cdot dh \\ &= \frac{2\pi r h}{3} \cdot (0.02) r + \frac{\pi r^2}{3} \cdot (0.01)h \\ &= \frac{\pi r^2 h}{3} \cdot 0.05 = 0.05 V \end{aligned}\]따라서 부피는 5%씩 증가한다. $\blacksquare$
Directional Derivative
이변수 함수 $z = f(x, y)$의 미분을 생각할 때, 편미분 $f_x$, $f_y$는 $x$축/$y$축라는 특정 방향에서의 순간변화율을 얻을 수 있다. 그런데, 2차원에선 정말 많은 방향으로 그 점을 지나칠 수 있다. 예를 들어, $y = x$ 방향으로의 순간변화율을 얻고 싶을 수도 있고, $y = 2x$ 방향으로의 순간변화율을 얻고 싶을 수도 있다.
그래서 이변수 함수 $z = f(x, y)$의 어떤 방향 벡터 $\vec{u} = \left<a, b\right>$ 방향으로의 순간변화율을 계산한 것이 “방향 도함수(Directional Derivative)“다.
만약 뱡항 벡터가 $u = \left<1, 0\right>$라면, 방향도함수는 $x$축에 대한 편미분 $f_x$가 된다. $y$축에 대해서도 마찬가지.
방향도함수에서 대한 위의 정의를 이용해도 되지만, $x$, $y$축에 대한 편도함수를 사용하면 더 쉽게 방향도함수를 계산할 수 있다.
이것은 편도함수과 방향도함수의 개념을 연결해주는 중요한 성질이다.
Gradient Vector
방향도함수와 편도함수를 연결한 위의 식을 자세히 살펴보면… 뭔가 내적(dot product) 같은 느낌이 솔솔 난다 ㅋㅋ
그래서 방향도함수를 아래와 같이 표현할 수 있다.
\[D_u f(x, y) = \left<f_x(x, y), f_y(x, y)\right> \cdot \left<a, b\right>\]이때, 방향벡터와 내적하는 왼쪽의 벡터에 “Gradient Vector“라는 이름을 붙여주자. 요 벡터는 함수 $f(x, y)$를 $x$축, $y$축 방향으로 편미분한 편도함수를 각각의 성분으로 갖는다.
How to maximize the directional derivative
Direction Derivative는 Gradient Vector $\nabla f$와 방향 벡터 $\mathbf{u}$의 내적으로 정의되었다. 이 값을 최대화 하려면 어떻게 해야 할까?
정답은 방향 벡터 $\mathbf{u}$가 “Gradient Vector”와 평행한 벡터일 때 Direction Derivative의 크기가 가장 커진다.
\[\text{max size when } \nabla f \parallel \mathbf{u}\]이 사실을 바탕으로 우리는 이변수 함수가 있을 때, 어떤 방향으로 가야 함숫값이 가장 커지는 방향으로 갈 수 있는지 알 수 있게 된다. 만약 지금 위치하는 점에서의 방향 벡터 방향만 움직인다면, 그것이 함수의 최대값에 가장 빠르게 도달하는 방법이다. 만약, 최솟값에 빠르게 도달하고자 한다면, 방향 벡터와 반대 방향으로 움직이면 된다. (이것에서 유래한 것이 머신러닝에서 사용하는 “Gradient Descent” 방식이다.)