Lagrange Multiplier

복수전공하고 있는 수학과의 졸업시험을 위해 학부 수학 과목들을 다시 공부하고 있습니다. 미적분학 포스트 전체 보기

A powerful method for finding extreme values of constrained functions

“라그랑주 승수법(Lagrange Multiplier)”라는 방법론은 제한 조건이 있는 상황에서 함수의 극값(extreme value)를 강력한 방법이다. 지금까지 앞장에서 배운 미적분학2 내용을 전부 바탕으로 하는 중요한 응용 사례 중 하나다.

The Lagrange Multiplier

picture from wikimedia

거두절미하고 바로 어떻게 하는 건지 바로 살펴보자.

이차원 평면 상에 함수 $z = f(x, y)$가 있다. 이 함수의 최대/최소 값을 구하는 것이 목표이다. 그런데 최대/최소 값을 함수의 정의역 전체가 아니라 특정 국소 범위에 안에서의 최대/최소 값을 찾고 싶다. 이때, 국소 범위는 영역(Region)이 아니라 $g(x, y) = k$라는 곡선으로 주어진 상황이다. 이 곡선 위에서 함수 $f(x, y)$의 최대/최소 값을 구해야 하며, $g(x, y) = k$를 제약조건(Constraint)라고 한다.

곡선 $g(x, y) = k$ 위에 존재하는 함수 $f(x, y)$의 최대/최소 값의 위치가 $(a, b)$라고 하자. 그러면, 위치 $(a, b)$는 아래의 아래의 등식을 만족한다.

\[g(a, b) = k\]

제약조건을 이루는 곡선 $g(x, y) = k$에 있으니 이건 당연하다.

\[\nabla f = \lambda \nabla g\]

갑자기 Gradient Vector가 나왔다!! 위의 식은 최대/최소 위치 $(a, b)$에서 함수 $f(x, y)$와 $g(x, y)$의 Gradient Vector가 서로 같은(parallel) 방향을 바라본다는 것을 말한다. 평행을 표현하기 위해 $\lambda \in \mathbb{R}$로 표현한 것.

위와 같은 Gradient Vector가 평행한 상황이 나오는 이유는 제약조건 $g(x, y) = k$ 곡선과 함수 $f(x, y)$의 Level Curve $f(x, y) = z_0$가 서로 접하기 때문이다.

처음에는 Constraint Curve와 Level Curve가 접한다는 조건이 이해가 안 되었다. “꼭 접해야만 최대/최소가 있는건가?”라는 생각이 들었다. 그래서 찾아보니 stackexchange 사이트에서 요런 답변을 찾고 드디어 이해가 좀 되었다.

For $f(x, y) = d$, you increment value $d$ until you touch $𝑔(x, y)=c$. In the moment of contact you take a minimum. If you go on, just before $f(x, y) = d$ leaves the contact, you take the maximum.

즉, $f(x, y) = d_{min}$하는 점에서부터 점점 함숫값을 키우며 Level Curve를 확장하다가 $g(x, y) = k$와 접하는 그 순간이 minimum 순간이다. 여기서 Level Curve의 값을 더 늘리면 제약조건은 만족하지만 접하던 순간보다는 함숫값이 커져버린다.

picture from wikimedia

그림을 곁들여 함께 이해해보자.

\[\nabla f = \lambda \nabla g\]

Gradient Vector로 이뤄진 식은 벡터 등식이다. 따라서 이것을 풀기 위해선 성분별로 등식을 세워서 풀면 된다. 처음의 제약 조건 식까지 같이 적으면 아래와 같다.

\[\begin{aligned} f_x &= \lambda g_x \\ f_y &= \lambda g_y \\ g(x, y) &= k \end{aligned}\]

위의 연립방정식을 풀면 제약조건 위에서의 최대/최소값과 그 위치를 알 수 있다. 위의 연립식에서 구해야 할 미지수는 최대최소값의 위치 $(x, y)$ 뿐만 아니라 multiplier인 $\lambda$의 값도 미지수로서 그 값을 찾아야 한다. 이때 $\lambda$는 그 값을 찾아도 별 의미는 없지만 방정식을 풀다보면 그 값을 반드시 찾아야 한다는 걸 깨닫게 된다. (예제에서 느끼게 될 것.)

Constrained Maxima/Minima

Find the point $(x, y, z)$ on the plane $2x + y - z = 5$ that is closest to the origin.

평면 $g(x, y, z) = 5$ 위에 있으면서도 distance 함수 $d(x, y, z) = x^2 + y^2 + z^2$의 값을 최소화 하는 점 $p(x, y, z)$를 찾아야 한다. Lagrange Method를 사용해 Gradient에 대한 식 $\nabla d = \lambda \nabla g$을 세우면

\[\begin{aligned} 2x &= 2 \lambda \\ 2y &= \lambda \\ 2z &= - \lambda \\ \end{aligned}\]

이것을 $g(x, y, z) = 2x + y - z = 5$에 대입하면, $2 \lambda + \lambda/2 + \lambda/2 = 5$가 되고, $\lambda = 5/3$이 된다.

이를 바탕으로 다시 $(x, y, z)$에 대입하면, closest point $(x, y, z) = (5/3, 5/6, -5/6)$가 된다. $\blacksquare$

Lagrange Method with Two Constraints

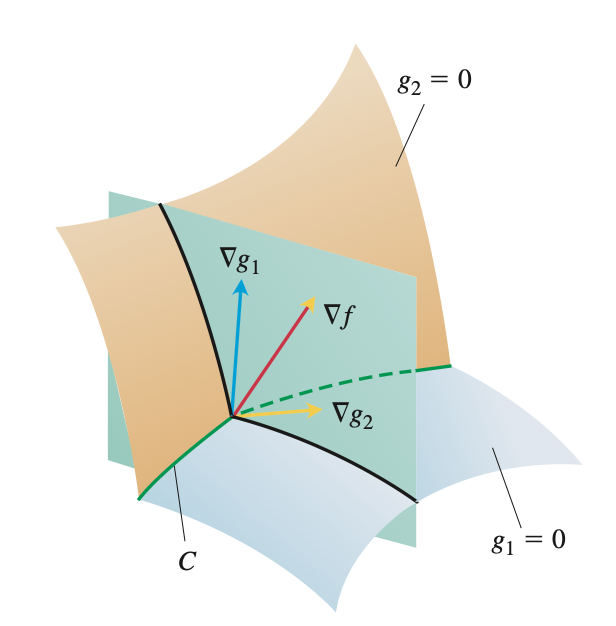Thomas Calculus 13th ed.

어떤 경우는 제약 조건이 2개 존재할 수도 있다.

\[g_1(x, y, z) = 0 \text{ and } g_2(x, y, z) = 0\]

이때 두 제약조건은 둘다 미분가능 하며, Gradient Vector가 서로 평행하지 않아야 한다.

두 제약조건 $g_1 = 0$와 $g_2 = 0$가 서로 교차하여 생긴 곡선 $C$를 생각해보자. 우리는 이 곡선 $C$ 위에서 함수 $f(x, y, z)$의 극대/극소 값을 찾아야 한다. 그리고, 곡선 $C$는 함수 $f(x, y, z)$와 접하는 지점에서 극대/극소 값을 갖는다. 이것은 제약조건이 하나 였을 때와 비슷한 패턴이다.

\[C \perp \nabla f\]

또, 곡선 $C$는 $\nabla g_1$, $\nabla g_2$와도 수직 관계를 이룬다. 이것은 곡선 $C$가 제약조건을 이루는 평면 위에 존재하기 때문이다.

\[C \perp \nabla g_1 \text{ and } C \perp \nabla g_2\]

위의 두 사실을 바탕으로 $\nabla f$가 서로 평행하지 않은 두 벡터 $\nabla g_1$, $\nabla g_2$가 이루는 평면 위에 있음을 생각해볼 수 있다. 따라서 아래와 같은 일차 결합 식이 유도된다.

\[\nabla f = \lambda \nabla g_1 + \mu \nabla g_2\]

예제를 통해 좀더 익혀보자.

The plane $x + y + z = 1$ cuts the cylinder $x^2 + y^2 = 1$ in an ellipse. Find the points on the ellipse that lie closest to and farthest from the origin.

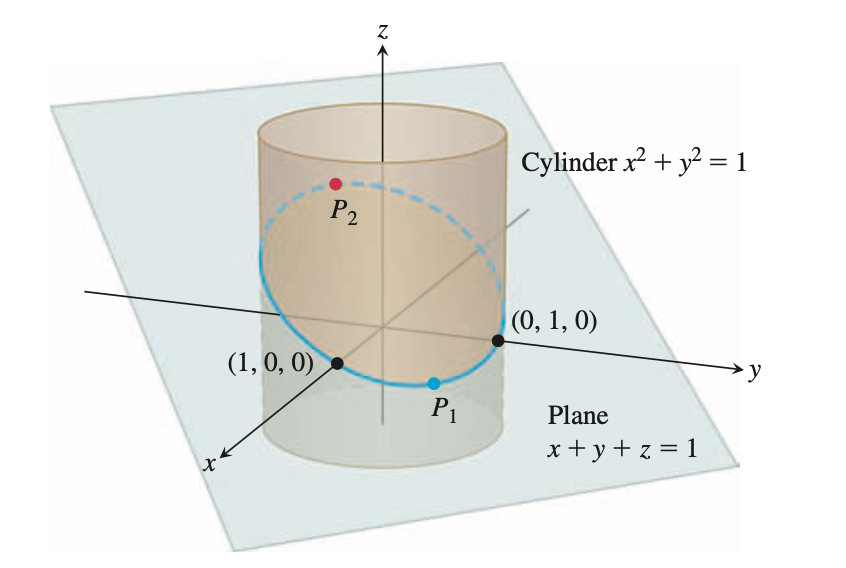Thomas Calculus 13th ed. - Example Problem

제약 조건과 거리 함수를 정의하자.

\[\begin{aligned} g_1 &= x + y + z - 1 = 0 \\ g_2 &= x^2 + y^2 - 1 = 0 \\ d &= x^2 + y^2 + z^2 \end{aligned}\]

Lagrange Method에 따라 Gradient에 대한 성분으로 등식들을 세우자.

\[\begin{aligned} \lambda + 2x \mu &= 2x \\ \lambda + 2y \mu &= 2y \\ \lambda &= 2z \\ \end{aligned}\]

위의 등식에 $\lambda = 2z$를 대입하고 정리하면

\[\begin{aligned} z &= x(1 - \mu) \\ z &= y(1 - \mu) \\ \end{aligned}\]

위의 등식은 2가지 경우에서 성립하게 되는데,

1. $z = 0$이고, $\mu = 1$
2. $x = y$이고, $\mu \ne 1$

1번의 경우는 $\lambda = 2z = 0$이 되고, 지점은 $(1, 0, 0)$ 또는 $(0, 1, 0)$이 된다. 그림에서 $x$축, $y$축 위에 있는 점들이며, closest point를 이룬다.

2번의 경우는 $x = y = \pm \frac{1}{\sqrt{2}}$가 되며, $z = 1 \mp \sqrt{2}$가 된다. 그림에서 $P_1$, $P_2$가 바로 그 점들이며, farthest point를 이룬다.