Multiple Integrals
복수전공하고 있는 수학과의 졸업시험을 위해 학부 수학 과목들을 다시 공부하고 있습니다. 미적분학 포스트 전체 보기
Fubini’s Theorem
If $f$ is continuous on the rectangle
\[R = \{ (x, y) \| a \le x \le b, c \le g \le d\}\]then
\[\underset{R}{\iint} f(x, y) \, dA = \int_{a}^{b} \int_{c}^{d} f(x, y) \, dy dx = \int_{c}^{d} \int_{a}^{b} f(x, y) \, dx dy\]즉, 함수가 직사각형의 정의역 안에서 연속성을 가지는 적당한 함수라면, 적분 순서를 $x$ 먼저 하든, $y$ 먼저 하든 상관 없이 같은 적분 값이 나온다는 걸 말한다.
Double Integral Over General Region
위의 경우는 적분 영역 $R$이 ‘직사각형’의 나이스한 형태로 주어진 경우다. 이런 이중 적분은 정말 쉽다. 그러나 많은 경우, 적분 영역은 자유분방한 형태로 존재한다. 특히 $y = g(x)$의 관계를 만족하거나,$x = h(y)$의 관계를 만족하는 적분 영역을 마주하는 경우가 많을 것이다.
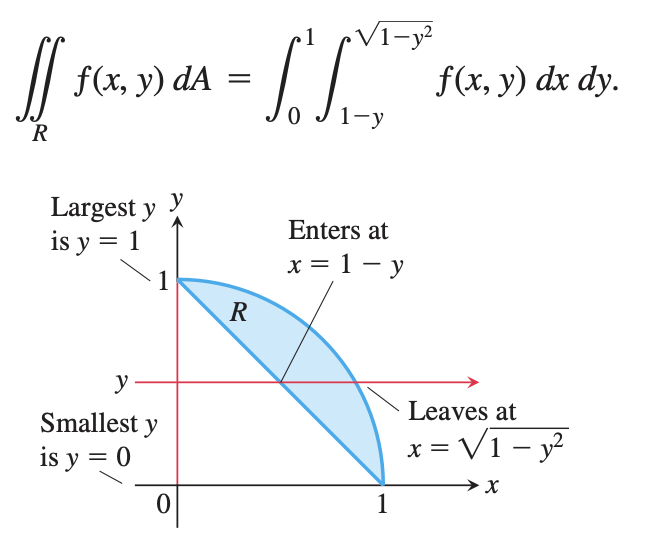Thomas Calculus 13th ed. - Example Problem
이 경우는 $x = h(y)$의 꼴로 적분 영역이 표현되는 경우에 해당한다. 그래서 $x$ 축 방향으로 먼저 적분을 수행한 후에, $y$ 축 방향으로 적분을 수행한다.
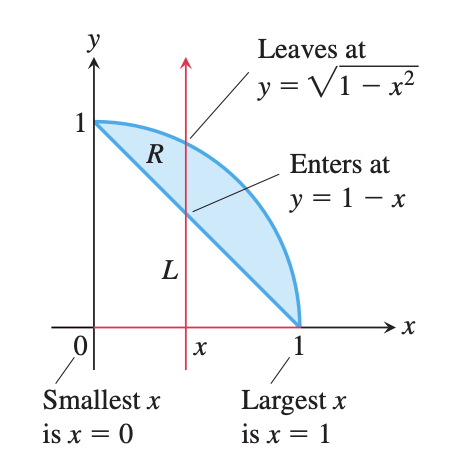Thomas Calculus 13th ed. - Example Problem
위의 예제는 반대로 $y = g(x)$ 꼴로 표현하여 해결할 수도 있다. 이 경우는 $y$ 축 방향으로 먼저 적분 후 $x$ 축 방향으로 적분을 수행한다.
Double Integrals in Polar Form
어떤 함수들은 원점을 기준으로 하는 극좌표계로 편리하여, 적분도 극좌표계를 기준으로 수행하는게 더 쉬운 경우도 있다.
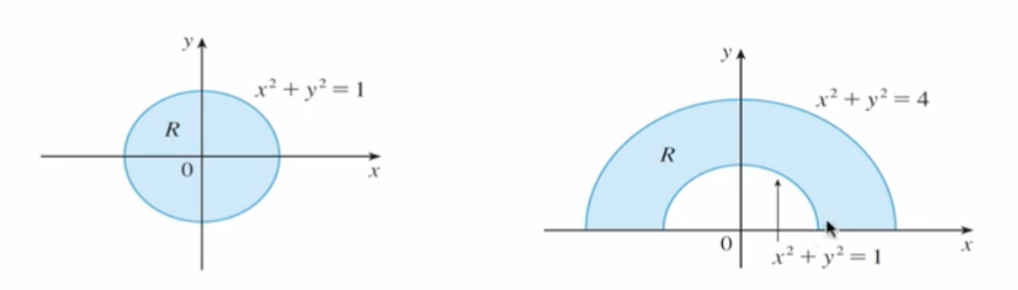
위와 같은 경우, 극좌표계로 표현하면
- $R = \{ (r, \theta) | 0 \le r \le 1, \; 0 \le \theta \le 2 \pi \}$
- $R = \{ (r, \theta) | 1 \le r \le 2, \; 0 \le \theta \le \pi \}$
와 같이 $xy$-좌표계에서 직사각형을 표현하는 것처럼 쉽게 영역 $R$를 표현할 수 있다. 그래서 이런 형태의 영역을 “Polar Rectangle“이라고 부른다 ㅋㅋ
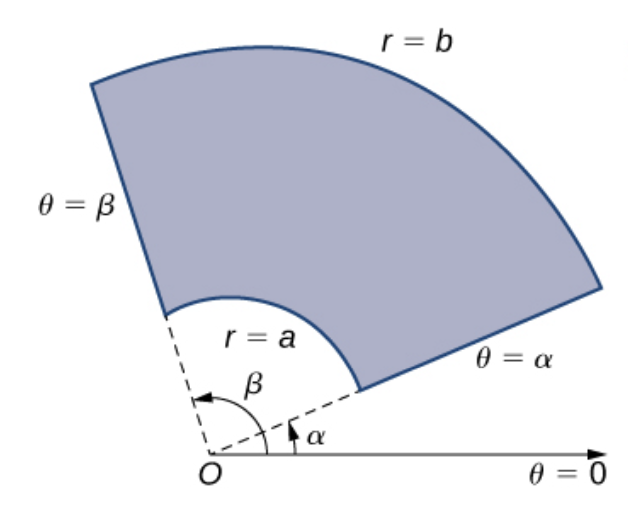Gilbert Strang - Calculus Vol 3.
이때, $xy$ 좌표계에서의 적분과 달리 극좌표에서의 적분은 아래와 같이 변환이 필요하다.
\[\underset{R}{\iint} f(x, y) \, dx dy = \underset{R}{\iint} f(r, \theta) \cdot r \cdot dr d\theta\]위의 식을 보면, 미분소가 $dx dy = r \cdot dr d\theta$이 되는데,
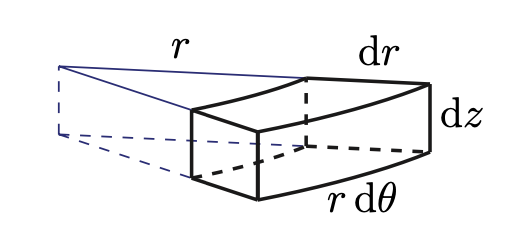
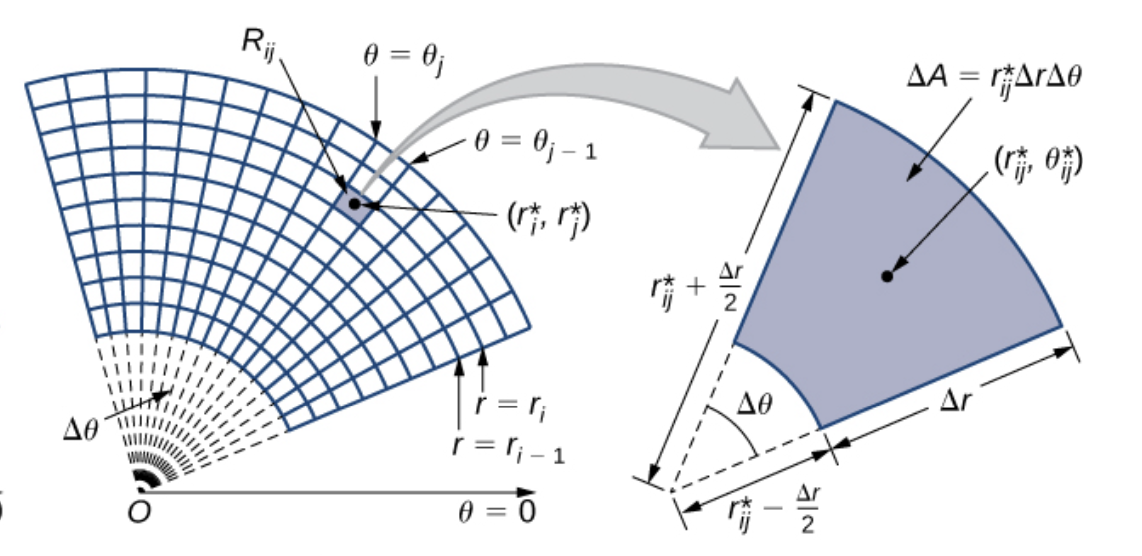Gilbert Strang - Calculus Vol 3.
위와 같이 Polar Rectangle의 미소변화량을 $dA$를 계산해보면, $r \cdot dr d\theta$의 꼴이 되기 때문이다.
Triple Integrals
만약 적분 영역이 아주 나이스 하다면, 삼중 적분을 그냥 $x$, $y$, $z$에 데이터 적분을 세 번 하면 된다.
\[\underset{D}{\iiint} f(x, y, z) dV = \int_{r}^{s} \int_{c}^{d} \int_{a}^{b} f(x, y, z) \, dx \, dy \, dz\]당연하게도 현실에서 위와 같이 단순한 경우는 거의 없다. (이젠 익숙하다;;)
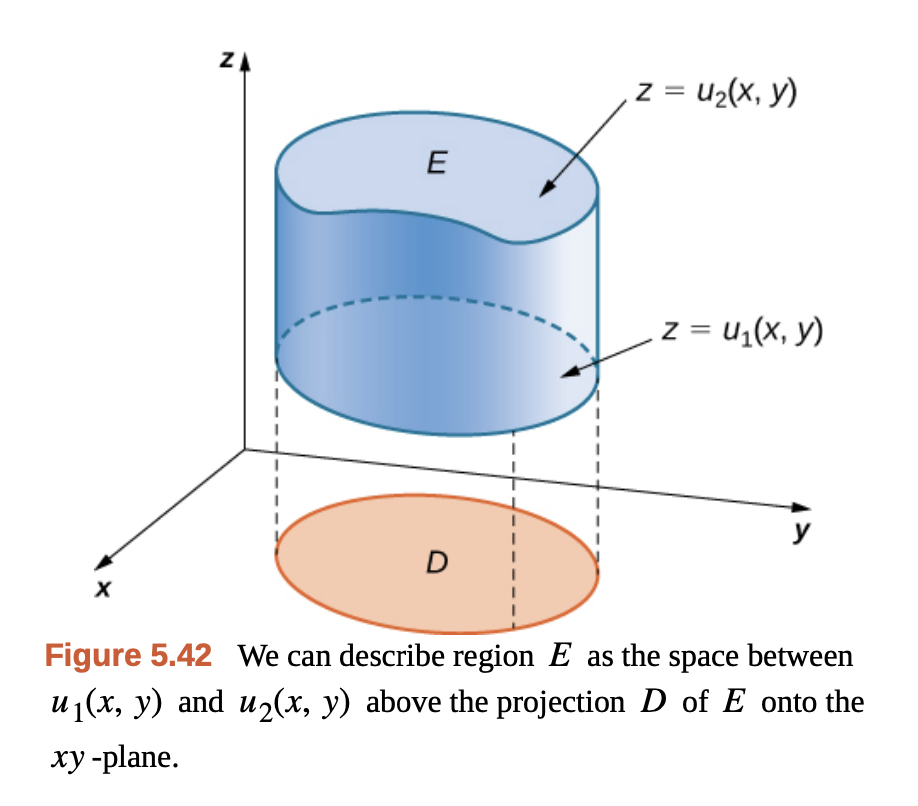Gilbert Strang - Calculus Vol 3.
3차원 물체의 위-아래 뚜껑이 어떤 함수로 정해지는 경우다. 이 경우, 아래와 같이 적분 구간에 해당 함수를 넣어주면 된다.
\[\underset{D}{\iint} \left[ \int_{u_1(x, y)}^{u_2(x, y)} f(x, y, z) \, dz \right] \, dx \, dy\]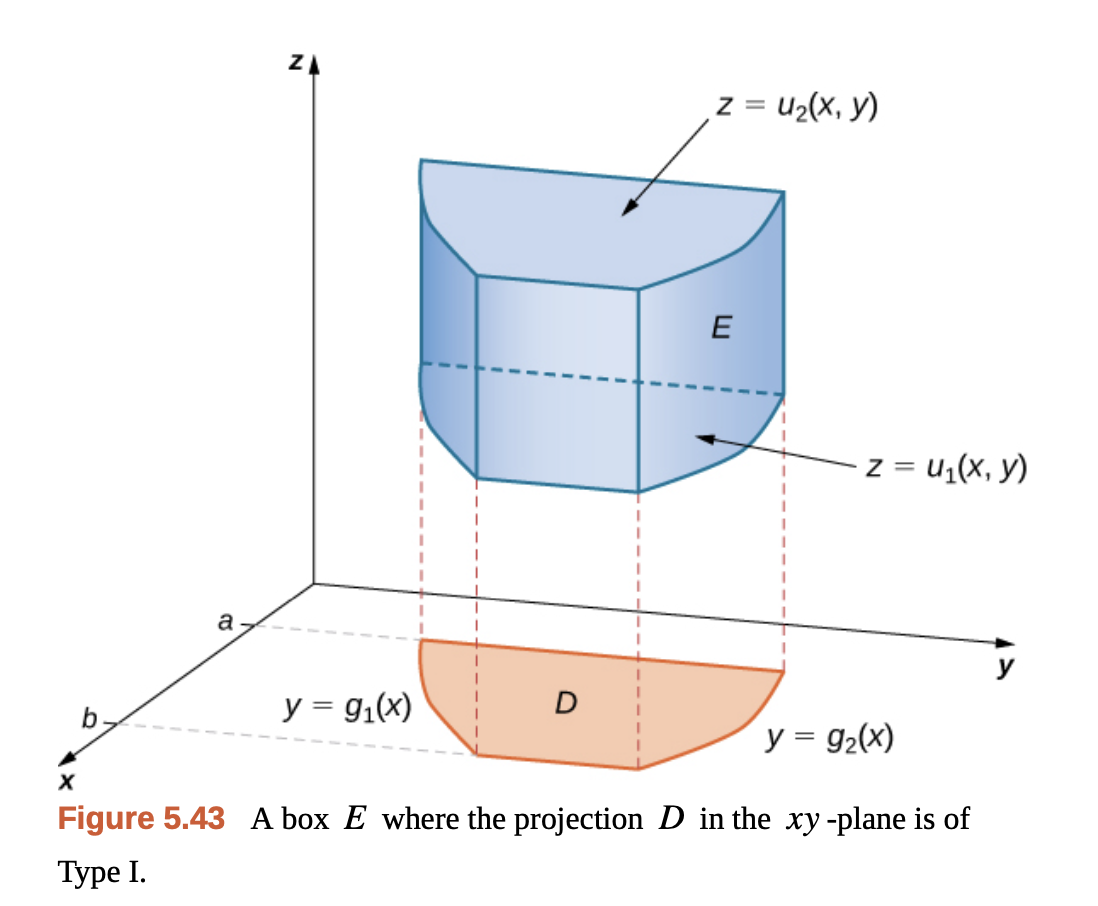
Gilbert Strang - Calculus Vol 3.
이중적분에서 했던 것처럼 $xy$ 평면의 영역 $D$가 $y = g(x)$ 꼴로 두 변수 간에 함수 관계가 있을 수도 있다. 이 경우는 삼중 적분이 아래와 같을 것이다.
\[\int_{a}^{b} \int_{g_1(x)}^{g_2(x)} \int_{u_1(x, y)}^{u_2(x, y)} f(x, y, z) \, dz \, dy \, dx\]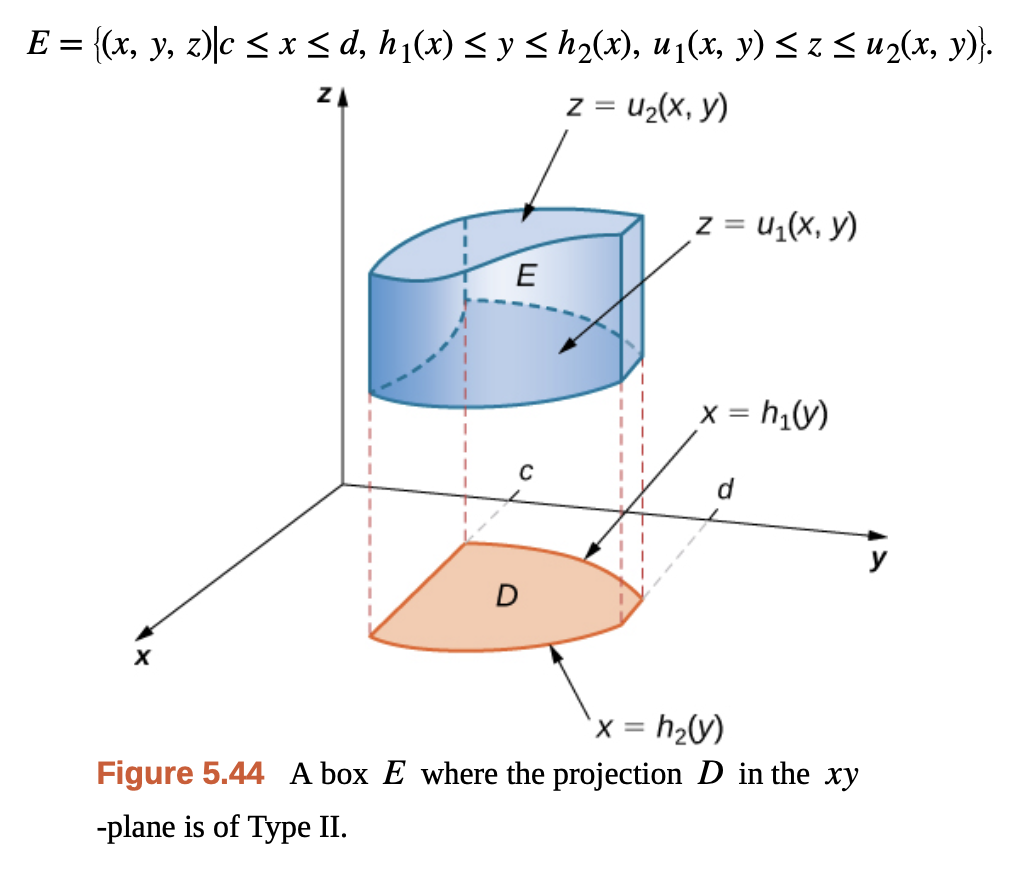
Gilbert Strang - Calculus Vol 3.
반대로 $x = h(y)$와 같은 종속 관계도 있을 수도 있다. 삼중 적분 식의 표현은 생략.
주의할 점은 삼중적분의 영역을 정의하는 물체 $V$의 위-아래 뚜껑이 항상 $u(x, y)$와 같이 $z$ 축이 아닐 수도 있다는 점이다. 위-아래 뚜껑이 $y$축을 따라서 존재할 수도 있고, $x$축을 따라서 존재할 수도 있다. 적분 영역이 항상 위의 그림과 같은 형태로 나올 거라고 착각하지 말 것!
Triple Integrals in Cylindrical Coordinates
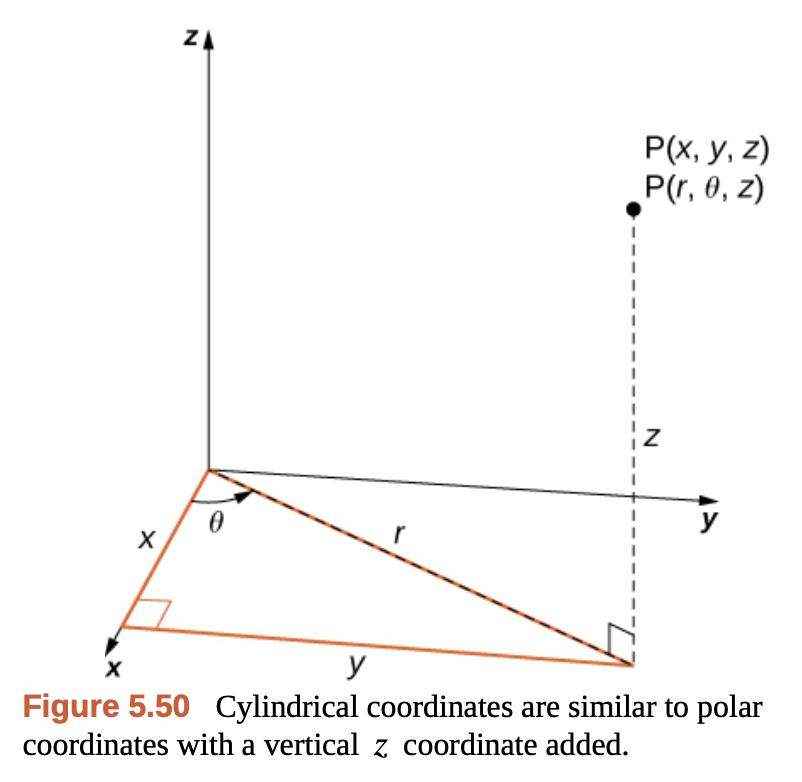Gilbert Strang - Calculus Vol 3.
3차원 상의 좌표를 $P(r, \theta, z)$로 표현하는 좌표계이다. 원점을 중심으로 하는 극좌표계로 표현되면서, 높이 $z$가 추가된 녀석으로 원기둥, 포물선 등을 표현하기에 쉬운 좌표계이다.
예를 들어, 아래와 같은 도형의 부피를 구하는 데에 적절하다.
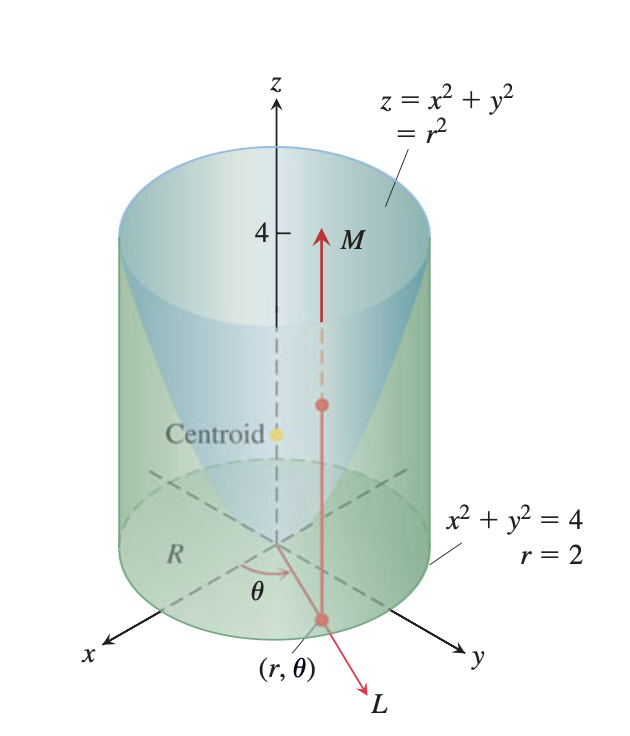Thomas Calculus 13th ed. - Example Problem
위의 도형의 경우, 부피를 구하기 위해서 아래의 적분을 수행한다.
\[V = \int_{0}^{2\theta} \int_{0}^{2} \int_{0}^{r^2} 1 \cdot dz \, r \, dr \, d\theta\]$z$축 방향으로 먼저 적분하고, 극좌표에 대한 적분을 수행한다.
Cylindrical Coordinates에서는 미소부피가 아래와 같이 표현된다.
\[\Delta V = \Delta z \cdot r \Delta r \cdot \Delta \theta\]
극좌표의 Polar Rectangular에서 높이 $\Delta z$만 추가된 꼴이다.
Triple Integrals in Spherical Coordinates
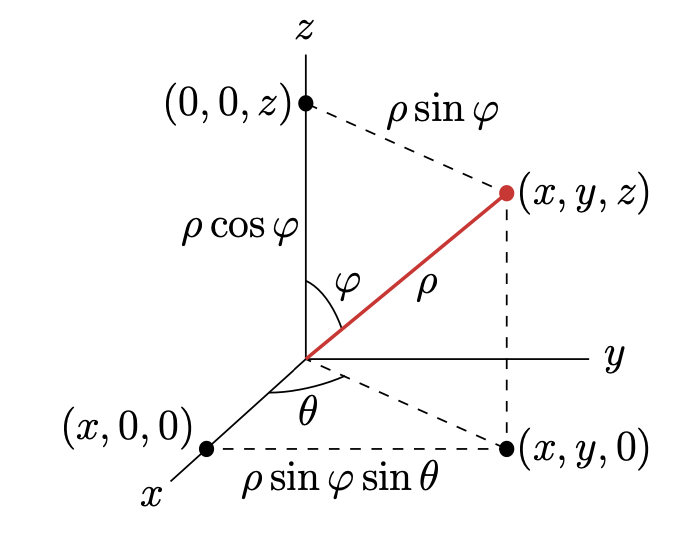
3차원 상의 좌표를 $P(\rho, \phi, \theta)$로 표현하는 좌표계이다. 원점을 중심으로 위도(longitude, $\theta$)와 경도(latitude, $\phi$)로 좌표를 표현한다. 이때, 헷갈리지 말아야 할 것은 극좌표계처럼 $(r, \theta)$가 아니라 원점으로부터 떨어진 길이 $\rho$를 사용한다는 점이다.
$xyz$ 좌표계에 대응하면 아래와 같다.
\[\begin{aligned} x &= \rho \sin \phi \cos \theta \\ y &= \rho \sin \phi \sin \theta \\ z &= \rho \cos \phi \end{aligned}\]구면좌표계는 아래와 같은 도형의 부피를 구하는 데에 적절하다. 아이스크림 콘 🍨
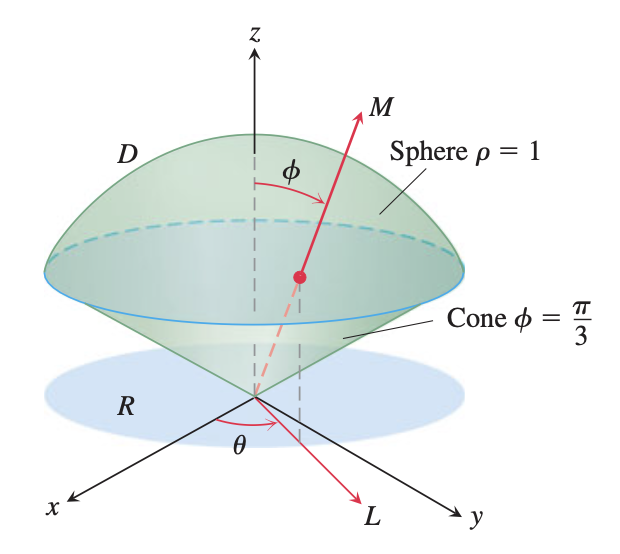Thomas Calculus 13th ed. - Example Problem
부피를 구하기 위해서 아래의 적분을 수행한다.
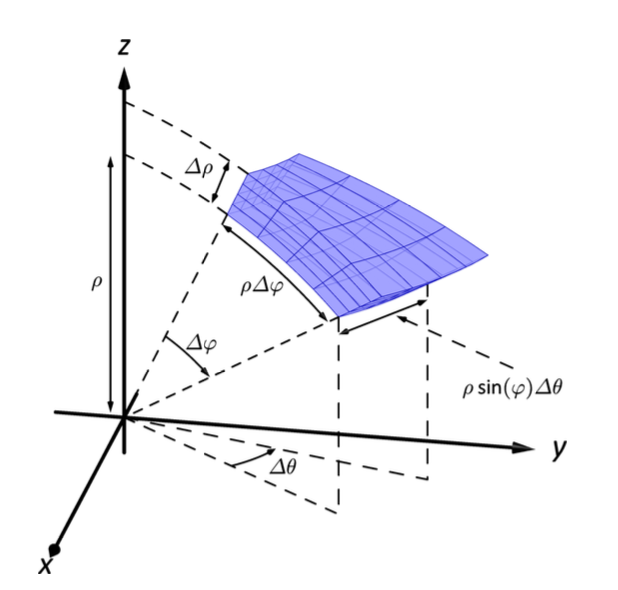
\[V = \int_{0}^{2\theta} \int_{0}^{\pi/3} \int_{0}^{1} 1 \cdot \rho^2 \sin \phi \cdot d \rho \, d \phi \, d\theta\]적분식에서 갑자기 $\rho^2 \sin \phi$가 튀어나왔는데, 요것은 미소 부피 변화량에서 유도된다.
\[\Delta V = \Delta \rho \cdot (\rho \, \Delta \phi) \cdot (\rho \, \sin \phi \, \Delta \theta)\]
혹시, $\rho^2 \sin \phi$가 기억이 안 난다면 요 “Spherical Wedge”의 부피가 유도되는 원리를 떠올리자 🙂
Transformation in a plane
1차원에서의 치환(Transformation)과 치환적분은 $x = g(t)$라는 식에서 아래와 같은 미소 변화량을 유도했다.
\[dx = g'(t) \, dt\]이런 1차원에서의 치환을 2차원에서 한번 생각해보자. 2차원 평면에서 $(u, v)$ 좌표를 $(x, y)$ 좌표로 변환하는 변환 함수 $T$를 상상 해보자.
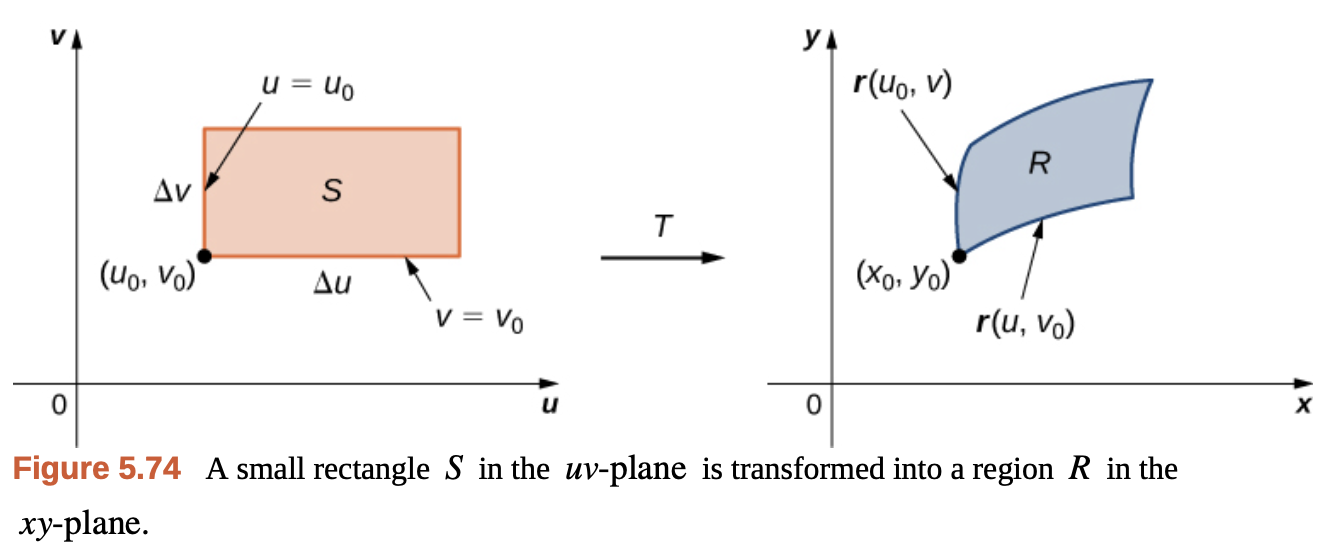Gilbert Strang - Calculus Vol 3.
이 함수를 벡터 함수 $\mathbf{r}(u, v)$의 형태로 표현해, 성분 별로 살펴보면 아래와 같다.
\[\mathbf{r}(u, v) = g(u, v) \mathbf{i} + h(u, v) \mathbf{j}\]$xy$ 평면 위의 점 $(x_0, y_0)$에서 영역 $R$의 lower side에서 그리는 곡선 $\mathbf{r}(u, v_0)$에 접하는 직선의 벡터를 구하면 아래와 같다.
\[\mathbf{r}_u = g_u(u_0, v_0) \mathbf{i} + h_u(u_0, v_0) \mathbf{j}\]같은 방식으로 영역 $R$에서 left side의 곡선에 접하는 직선 벡터를 구하면 아래와 같다.
\[\mathbf{r}_v = g_v(u_0, v_0) \mathbf{i} + h_v(u_0, v_0) \mathbf{j}\]우리는 변환 $T$의 결과로 만들어진 영역 $R$의 넓이를 구하기 위해 아래와 같이 할선(secant line)을 그어서 근사치를 구할 수 있을 것이다.
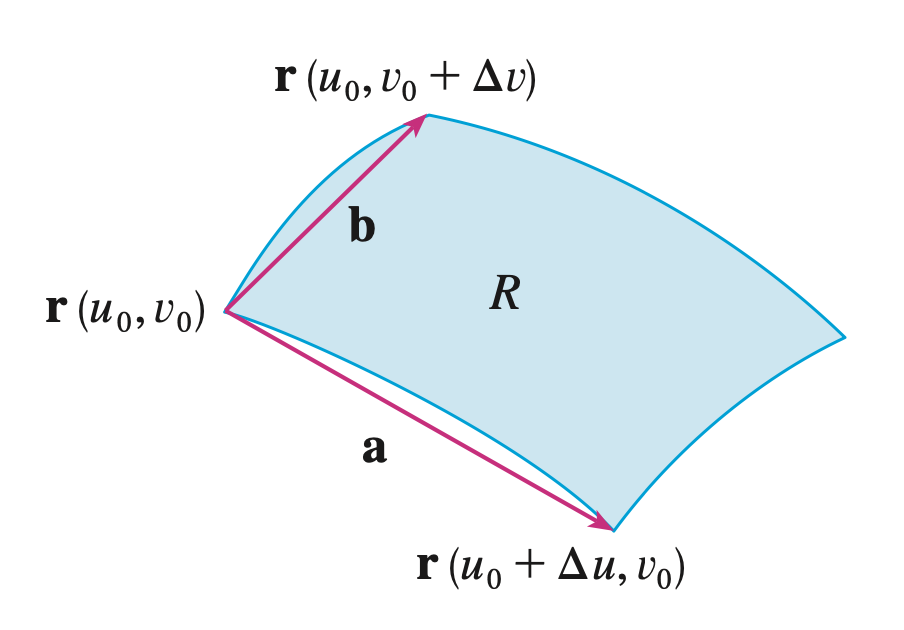Thomas Calculus 13th ed.
이 할선 벡터는 아래와 같이 주어질 것이다.
\[\begin{aligned} \mathbf{a} &= \mathbf{r}(u_0 + \Delta u, \, v_0) - \mathbf{r}(u_0, \, v_0) \\ \mathbf{b} &= \mathbf{r}(u_0, \, v_0 + \Delta v) - \mathbf{r}(u_0, \, v_0) \\ \end{aligned}\]이때, 아까 위에서 구한 접선 벡터 $\mathbf{r}_u$와 $\mathbf{r}_v$의 정의를 살펴보면,
\[\mathbf{r}_u = \lim_{\Delta u \rightarrow 0} \frac{\mathbf{r}(u_0 + \Delta u, \, v_0) - \mathbf{r}(u_0, \, v_0)}{\Delta u}\]위의 식을 활용해 $\Delta u$를 좌변으로 옮기면, 아래와 같은 근사식을 얻을 수 있다.
\[\begin{aligned} \Delta u \cdot \mathbf{r}_u &= \mathbf{r}(u_0 + \Delta u, \, v_0) - \mathbf{r}(u_0, \, v_0) \\ \Delta v \cdot \mathbf{r}_v &= \mathbf{r}(u_0, \, v_0 + \Delta v) - \mathbf{r}(u_0, \, v_0) \end{aligned}\]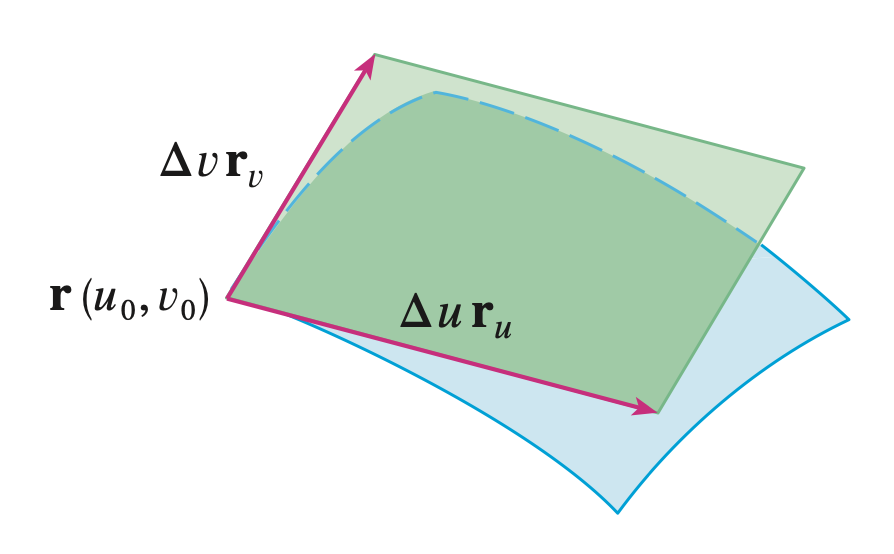
Thomas Calculus 13th ed.
위의 식을 활용해 영역 $R$의 넓이의 근사값을 두 벡터 $\Delta u \cdot \mathbf{r}_u$, $\Delta v \cdot \mathbf{r}_v$의 외적으로 구할 수 있다.
\[\left| (\Delta u \cdot \mathbf{r}_u) \times (\Delta v \cdot \mathbf{r}_v) \right| = \left| \mathbf{r}_u \times \mathbf{r}_v \right| \cdot \Delta u \Delta v\]이제 남은 건 외적 $\mathbf{r}_u \times \mathbf{r}_v$를 구하는 것이 남았다. 이것은 아래와 같은 행렬식을 구하는 것이다.
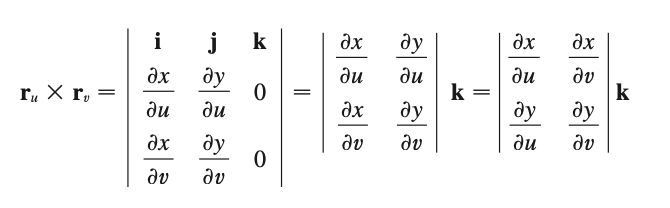Thomas Calculus 13th ed.
Jacobian
2차원에서의 변환 $T$에서 외적 $\mathbf{r}_u \times \mathbf{r}_v$의 행렬식을 “Jacobian”라고 부른다. 정의는 아래와 같다.
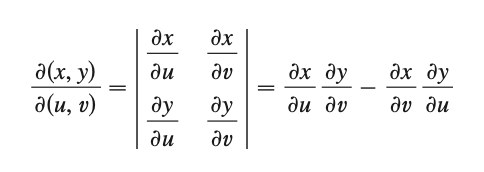
그리고 변환 $T$로 인해 만들어지는 넓이 미소변화량을 아래와 같이 Jacobian으로 쉽게 표기할 수 있다.
\[\Delta A = \left| \frac{\partial(x, y)}{\partial(u, v)} \right| \Delta u \Delta v\]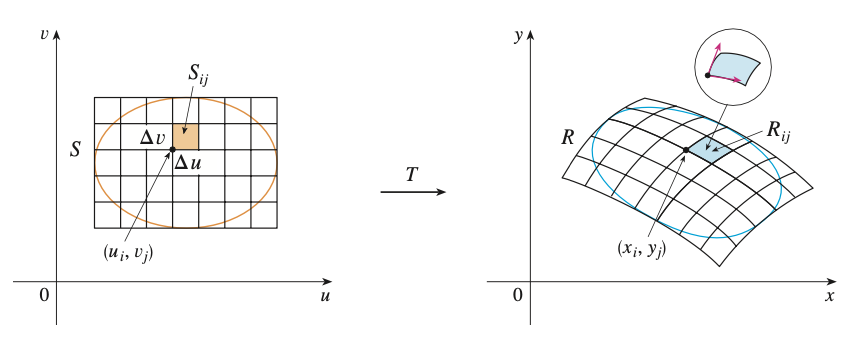
Thomas Calculus 13th ed.
이제 이를 바탕으로 이중 적분식에서 치환 적분을 했을 때, 적분식이 어떻게 변하는지 적어보면 아래와 같다.
\[\underset{R}{\iint} f(x, y) dA = \underset{R}{\iint} f(x(u, v), y(u, v)) \left| \frac{\partial(x, y)}{\partial(u, v)} \right| du dv\]넓이 미소변화량이 $dA$도 함께 치환된다…!!
3차원 치환에서도 야코비안이 정의되고, 이것을 삼중적분에 활용할 수 있지만… 포스트가 넘 길어졌으니 이젠 생략…!!