Vector Fields, and Line Integrals

복수전공하고 있는 수학과의 졸업시험을 위해 학부 수학 과목들을 다시 공부하고 있습니다. 미적분학 포스트 전체 보기

Gradient Fields

어떤 2변수 함수 $f(x, y)$가 있다고 하자. 이전 챕터에서 이 2변수 함수의 한 점 $(x_0, y_0)$에서 정의한 Gradient Vector를 기억하는가?

\[\nabla f(x, y) = f_x(x, y) \, \mathbf{i} + f_y(x, y) \, \mathbf{j}\]

이것을 한 점이 아니라 함수 $f(x, y)$의 정의역 전체에서 정의한 것이 “Gradient Field”다. 이것은 스칼라 함수인 $z = f(x, y)$로부터 유도되는 벡터 필드(= 벡터 함수)다.

Conservative Vector Field, and Potential Function

반대로 어떤 벡터 필드는 그 원본이 어떤 스칼라 함수인 것들이 있다. 이런 벡터 필드를 “Conservative Vector Field”라고 한다. 이들은 Gradient $\nabla$ 되기 전의 원시 스칼라 함수를 찾을 수도 있다.

A vector field $\mathbf{F}$ is called a “conservative vector field” if it is the gradient of some scalar function.

이런 Conservative Vector Field의 원시 스칼라 함수는 “Potential Function“라고 부른다.

Line Integrals

어떤 곡선을 따라 함수 $f(x, y)$에 적분을 수행하는 것을 “선적분”이라고 한다.

Scalar Line Integral

\[\int_C f(x, y) \, ds = \int_C f(x(t), y(t)) \cdot \sqrt{x'(t)^2 + y'(t)^2} \, dt\]

Vector Line Integral

\[\int_C \mathbf{F}(x, y) \cdot d\mathbf{r} = \int_C \mathbf{F}_1 \, dx + \mathbf{F}_2 \, dy + \mathbf{F}_3 \, dz\]

선적분 부분은 공부하다가 너무 헷갈려서 별도 포스트로 정리했다. 선적분에 대한 자세한 내용은 아래 포스트 참고 ㅎㅎ

➡️ Arc Length와 Line Integral

Fundamental Theorem for Line Integrals

Let $C$ be a smooth curve given by the vector function $\mathbf{r}(t)$ for $a \le t \le b$.

Let $f(x, y)$ be a differentiable function of two or three variables whose gradient vector $\nabla f$ is continuous on $C$.

Then,

\[\int_{C} \nabla f \cdot d\mathbf{r} = f(\mathbf{r}(b)) - f(\mathbf{r}(a))\]

$f(x)$의 적분을 시작점과 끝점에서의 원시함수 $F(x)$의 값의 차이로 구할 수 있다는 미적분학의 기본정리의 선적분 버전이다. 선적분에서는 적분하려는 함수가 Gradient Field라면, 시작점과 끝점에서 원시함수의 값의 차이로 적분을 구할 수 있다는 정리이다. 적분이 무지무지 쉬워진다는 말!!

적분하려는 함수가 Gradient Field라는 말은 곧, 그 함수가 “Conservative Vector Field”임을 말한다. 즉, Conservative Vector Field에서 성립하는 정리가 “선적분의 기본정리”인 것. 적분값을 계산하기 위해서 적절한 Potential Function만 찾으면 된다.

Work done by Gravitational Field

Find the work done by the gravitational field

\[\mathbf{F}(\mathbf{x}) = - \frac{mMG}{\| \mathbf{x} \|^3} \mathbf{x}\]

in moving a particle with mass $m$ from $(0, 0, 0)$ to $(1, 1, 1)$ along a piecewise-smooth curve $C$.

위의 선적분을 계산하기 위해서 문제에 제시된 piecewise-smooth curve $C$를 찾을 필욘 없다. $\mathbf{F}(\mathbf{x})$의 Potential Function만 찾을 수 있다면, 선적분의 기본정리로 시점과 종점에서의 값으로 적분을 계산하면 되기 때문.

중력장 $\mathbf{F}(\mathbf{x})$의 potential function은 아래와 같이 정의할 수 있다.

\[f(x, y, z) = \frac{mMG}{\sqrt{x^2 + y^2 + z^2}}\]

potential function을 찾았으니 선적분의 기본정리로 적분을 계산해보자.

\[W = \int_C \mathbf{F} \cdot d\mathbf{r} = \int_C \nabla f \cdot d\mathbf{r} = f(1, 1, 1) - f(0, 0, 0) =\frac{mMG}{3}\]

Independent of Path

시점과 종점은 같지만, 경로가 서로 다른 piecewise-smooth curve $C_1$, $C_2$가 있다고 하자.

일반적인 벡터 필드에서는 두 선적분의 값이 같지 않다.

\[\int_{C_1} \mathbf{F} \cdot d \mathbf{r} \ne \int_{C_2} \mathbf{F} \cdot d \mathbf{r}\]

그러나 벡터 필드가 Conservative Vector Field라면, 두 선적분의 값이 같아진다.

\[\int_{C_1} \nabla f \cdot d \mathbf{r} = \int_{C_2} \nabla f \cdot d \mathbf{r}\]

왜냐하면, 두 선적분이 시점, 종점에서의 potential function의 값 차이로 계산되기 때문이다.

이것을 정리한 것이 아래의 문장이다.

Line integrals of a continuous conservative vector field with a differentiable potential function are “independent of path”.

On a Closed Curve

이번에는 닫힌 곡선 $C$에서 Conservative Vector Field의 적분을 살펴보자. 결론부터 말하면, 폐곡선에서의 선적분의 값은 항상 0이다.

\[\int_{C} \mathbf{F} \cdot d\mathbf{r} = 0\]

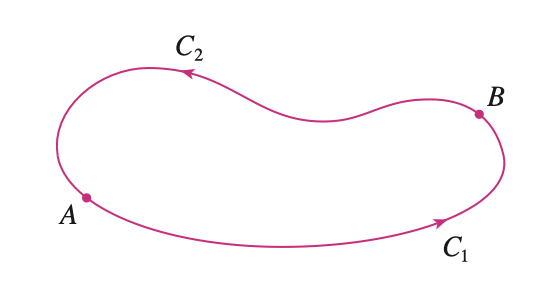
위의 선적분을 경로 $C_1$, $C_2$로 분할하여 생각하면 아래와 같기 때문.

\[\int_{C} \mathbf{F} \cdot d\mathbf{r} = \int_{C_1} \mathbf{F} \cdot d\mathbf{r} + \int_{C_2} \mathbf{F} \cdot d\mathbf{r} = \int_{C_1} \mathbf{F} \cdot d\mathbf{r} - \int_{-C_2} \mathbf{F} \cdot d\mathbf{r} = 0\]

(요기에서 opposite direction 적분 볼 때, 스칼라 선적분이랑 헷갈려서 한참 고민함… ㅋㅋ)

Theorems

Independent of Path implies Conservative

만약 주어진 벡터 필드의 적분이 주어진 도메인 $D$에서 모두 independent of path라면, 해당 벡터 필드는 도메인 $D$ 위에서 Conservative Field이다.

본래 Conservative Field면, Independent of path를 만족하는데, 그 역 명제도 성립함을 말한다.

If Conservative Field, then

만약 벡터 필드 $\mathbf{F} = P(x, y) \mathbf{i} + Q(x, y) \mathbf{j}$가 conservative vector field이고, $P$, $Q$ 함수가 도메인 $D$ 위에서 continuous first-order partial derivative를 가진다면, 아래 등식을 만족한다.

\[\frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x}\]

증명은 간단한데, 벡터 필드 $\mathbf{F}$가 conservative 하므로, 아래 식을 만족하는 potential function $f$가 존재한다.

\[\mathbf{F} = \nabla f\]

따라서 각 성분 $P$, $Q$는 아래와 같이 1차 편미분으로 정의된다.

\[\begin{aligned} P(x, y) &= \frac{\partial f}{\partial x} \\ Q(x, y) &= \frac{\partial f}{\partial y} \end{aligned}\]

이제, $P$, $Q$ 성분에 다시 $y$와 $x$에 대해 편미분 하면 아래와 같다.

\[\frac{\partial P}{\partial y} = \frac{\partial f}{\partial y \partial x} = \frac{\partial f}{\partial x \partial y} = \frac{\partial Q}{\partial x}\]

$\blacksquare$

Condition of conservative field

바로 위에서 살펴본 명제의 역 명제가 언제 성립하는지도 살펴보자.

Let $\mathbf{F} = P\mathbf{i} + Q \mathbf{j}$ be a vector field on an open simply-connected region $D$.

Suppose that $P$ and $Q$ have continuous first-order derivatives and satisfy $\frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x}$ throughout $D$.

Then, $\mathbf{F}$ is conservative.

주어진 벡터 필드가 Conservative 한지 판단하는 또 다른 방법이다. Conservative 여부를 판단하기 위해선 $P$, $Q$ 성분의 편미분 값이 일치한지를 확인하라는 말.

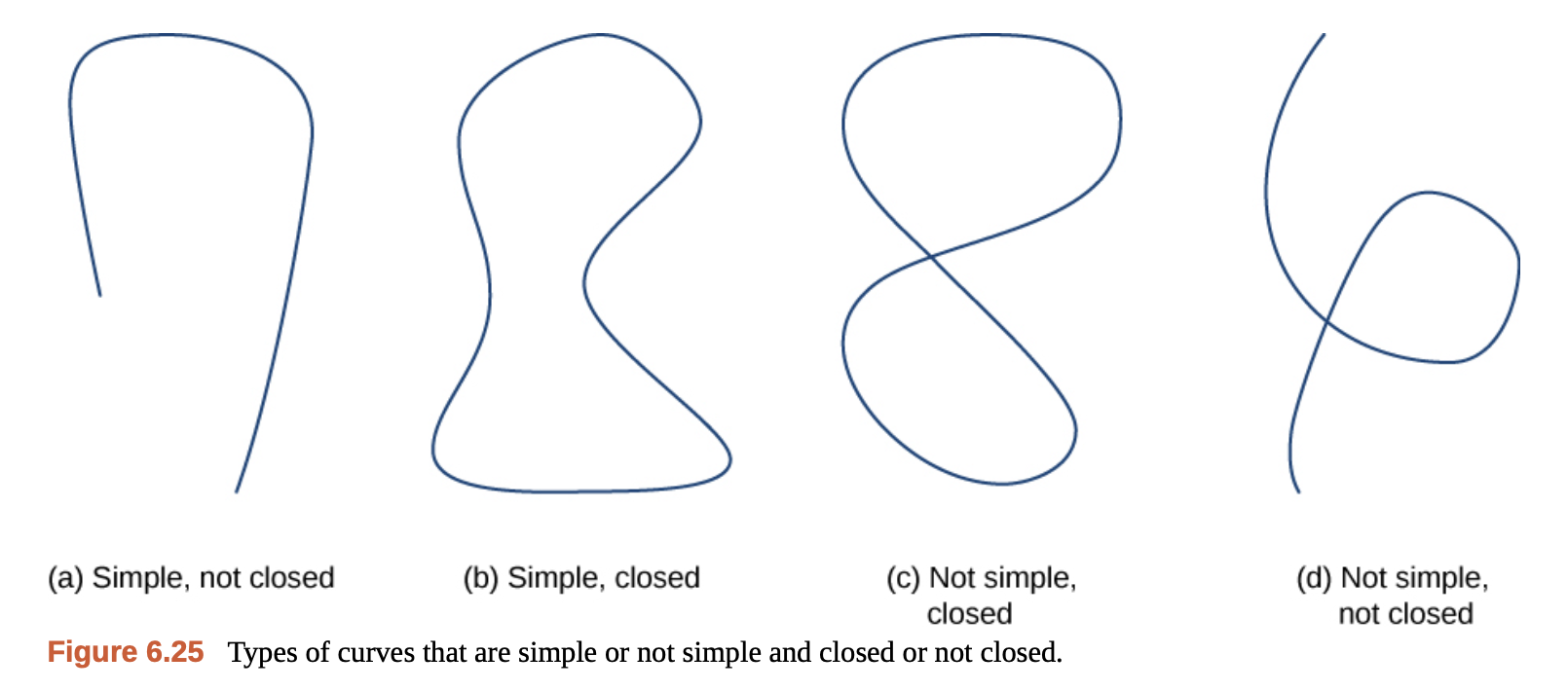
그런데 여기서 처음 등장한 개념이 “simply-connected region”이다. 대충 나눠서 설명하면,

Gilbert Strang - Calculus Vol 3.

“simple curve”는 곡선 자체가 자기 자신과 다시 만나지 않는 나이스한 곡선을 말한다.

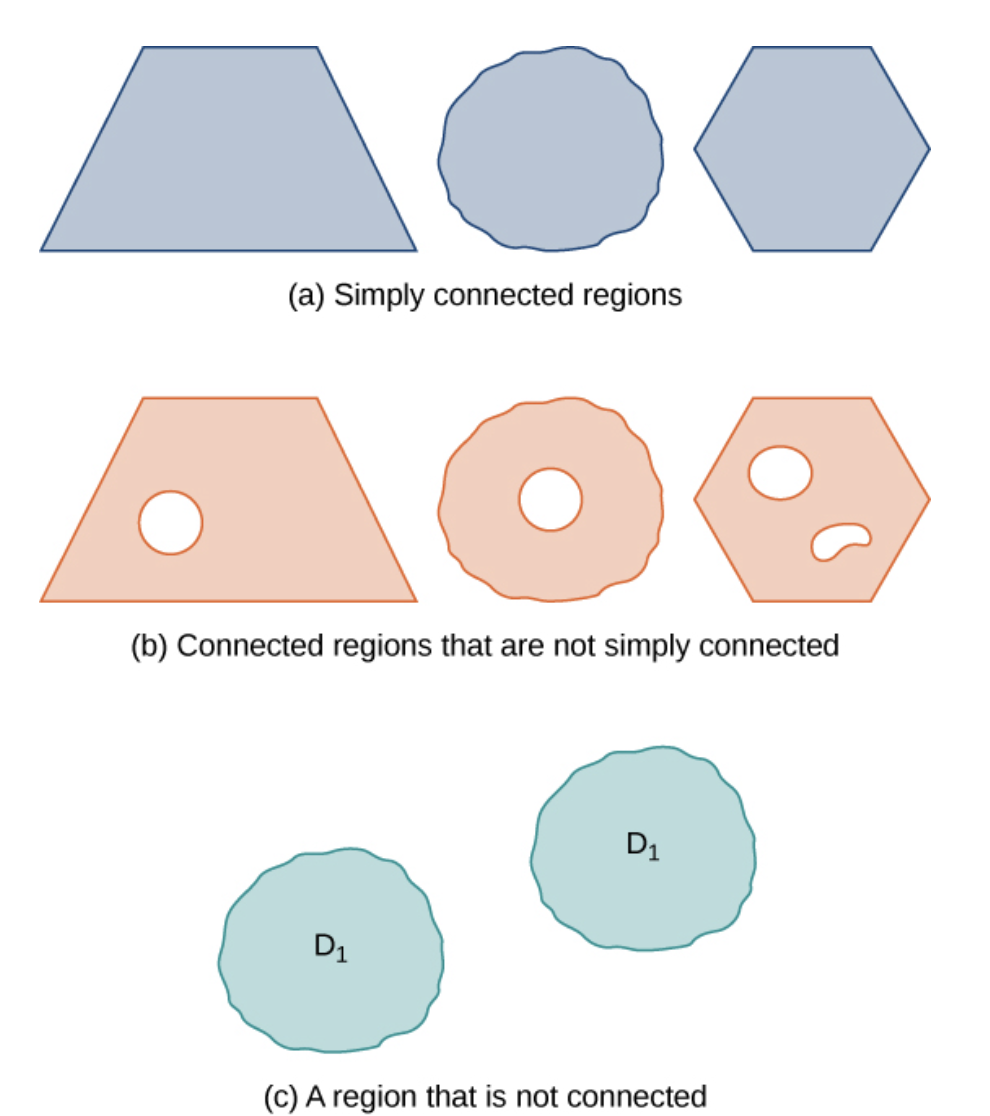
“simply-connected region”은 영역 위에 그릴 수 있는 모든 simple closed curve 안의 점이 모두 영역 $D$에 속하는 점들인 경우를 말한다.

Gilbert Strang - Calculus Vol 3.

만약 영역 안에 구멍(hole)이 있다면, 그 구멍을 둘러싸는 simple closed curve가 만드는 영역 안에는 영역 $D$에 속하는 점도 있겠지만, 속하지 않는 점도 생긴다. 따라서 2차원에서는 구멍 없는 영역을 일컫는다고 볼 수 있다.