Parametric Surface, and Surface Integral
복수전공하고 있는 수학과의 졸업시험을 위해 학부 수학 과목들을 다시 공부하고 있습니다. 미적분학 포스트 전체 보기
드디어 스토스크 정리를 들어가는 건가 싶었는데, 아직 공부할 게 더 남았다 ㅋㅋ 바로 “곡면 적분”… 요 포스트에서는 최대한 개념 위주로 적었는데, 교재에 있는 예제들을 풀어서 익숙해질 것을 아주아주 권장한다..!
매개 곡면이란
2차원, 3차원에서 매개 곡선을 정의하던 것을 기억하는가? 매개 곡선의 방정식은 아래와 같은 모습이었다.
매개 곡면은 2차원, 3차원에서 매개변수로 정의하는 곡선으로, 2개의 매개 변수가 필요하다.
이때, $u$ 변수를 고정하거나 $v$ 변수를 고정하면 매개 곡션의 방정식이 된다. 매개 곡면 위에 이 곡선들을 표현하면, 그리드 같은 모습으로 나타나고, 이를 “그리드 곡선(Grid Curve)“라고 부른다.
Gilbert Strang - Calculus Vol 3.
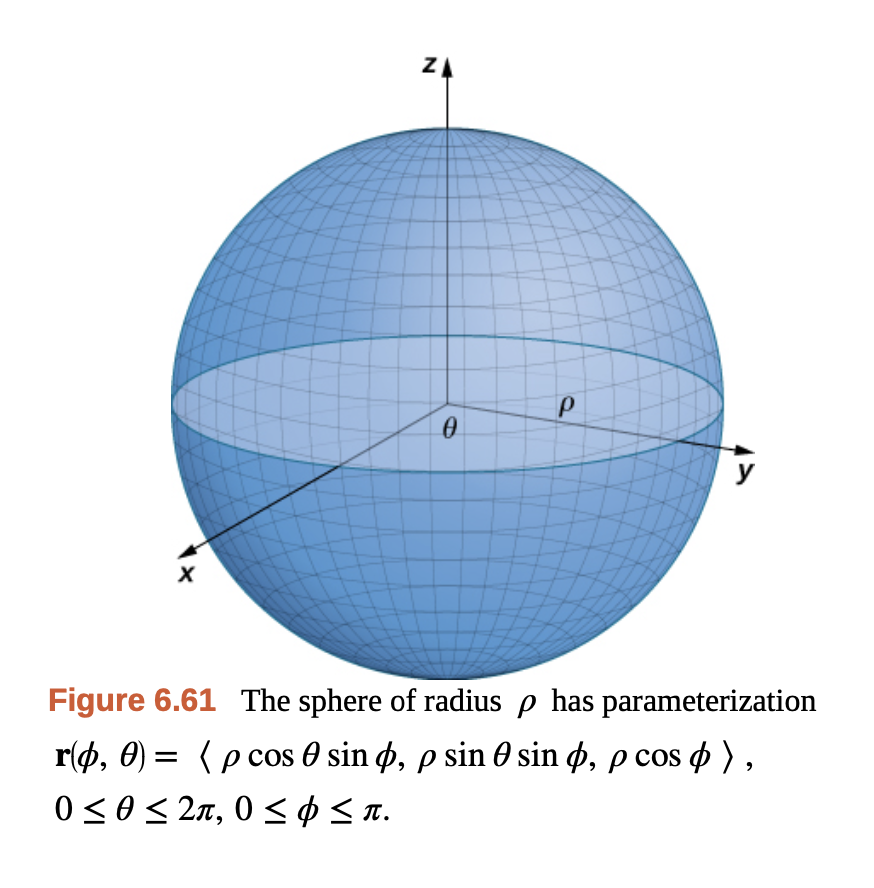
지구본이 그리드 곡선으로 표현되는 대표적인 매개 곡면이다. 위도와 경도를 통해 구 형태의 곡면의 방정식을 그리는 것.
매개 곡면의 넓이
Gilbert Strang - Calculus Vol 3.
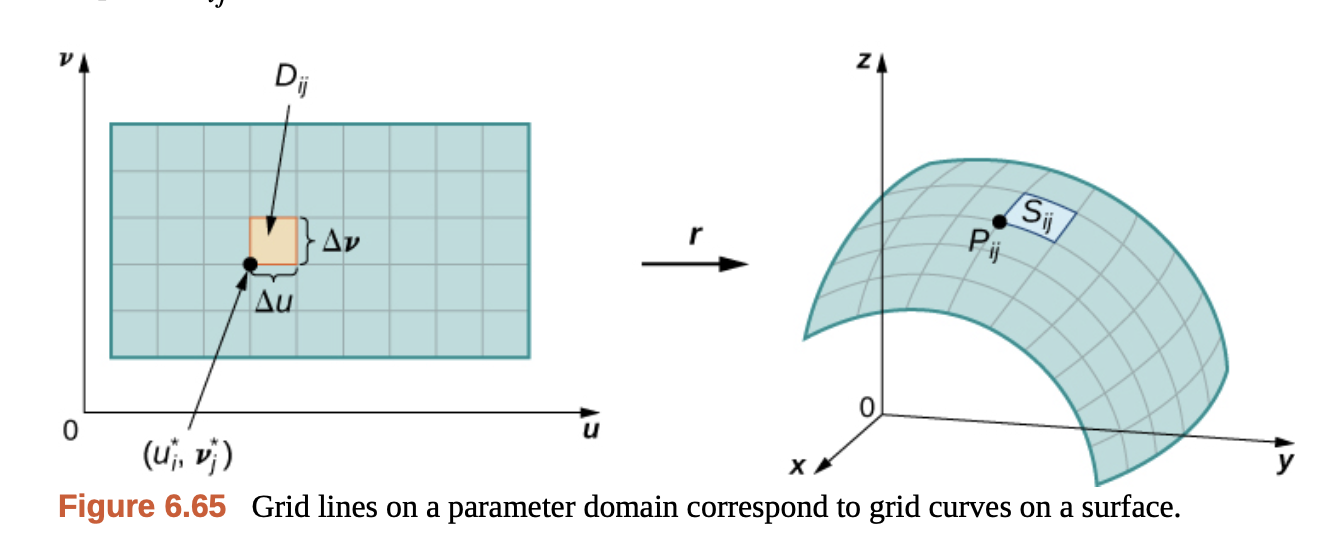
매개 변수 $(u, v)$의 영역에서의 미소 넓이 $dA = \Delta u \Delta v$가 매개 곡면 위에서는 $dS$로 표현된다. 그리고 이것은 아래와 같이 매개 변수에 대한 편미분에 대한 식으로 표현할 수 있다.
Gilbert Strang - Calculus Vol 3.
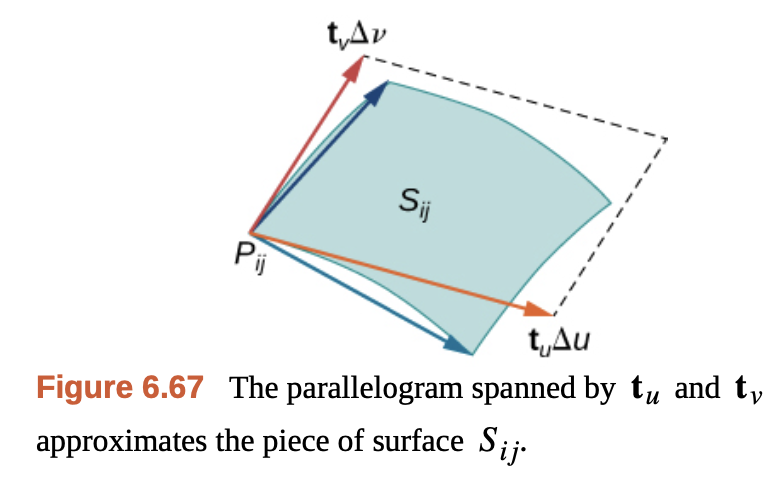
매개 곡면의 미소 넓이 $S_{ij}$는 아래의 식으로 근사할 수 있다.
\[S_{ij} \approx \left| (\mathbf{t}_u(P_{ij}) \cdot \Delta u) \times (\mathbf{t}_v(P_{ij}) \cdot \Delta v) \right|\]이를 다시 잘 정리하면, 아래와 같다.
이제 이걸 바탕으로 곡면의 넓이에 대한 식을 유도하면 아래와 같다.
\[\iint_{D} dS = \iint_{D} \left| \mathbf{t}_u \times \mathbf{t}_u \right| \, du \, dv\]사실상 xy 평면에서 정의한 매개 평면에 대한 넓이를 유도했던 것과 완전 동일하다! [Multiple Integrals: Transformation in a plane] 포스트에서 이에 대한 내용을 다뤘다. 외적인 부분도 사실 야코비안(Jacobian)이다.
\[J = \frac{\partial(x, y, z)}{\partial(u, v)} = \left| \mathbf{t}_u \times \mathbf{t}_u \right|\]매개 곡면 위 한 점에 대한 접평면의 방정식
Gilbert Strang - Calculus Vol 3.
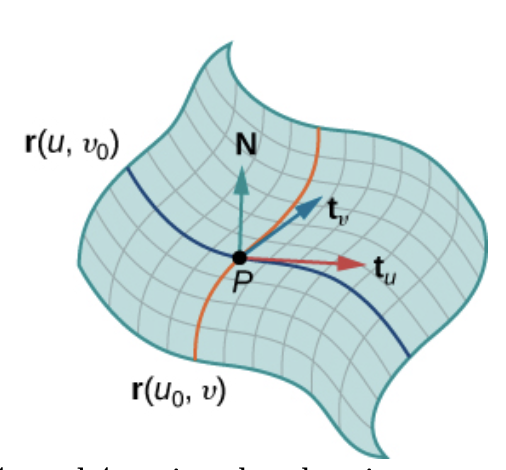
매개 곡면을 이루는 한 점에 대한 $u$와 $v$에 대한 Tangent Vector를 생각해보자. 매개 곡면 위의 접평면은 요 Tangent Vector의 외적으로 구해지는 노멀 벡터 $\mathbf{N}$를 활용하면 된다. EzEz
곡면의 방향
곡면의 방향(Orientation)을 결정하는 것도 간단하지만 중요한 문제다. 곡면은 two-side surface이기 때문에 어느 방향을 양(+)의 방향으로 잡는지 기준이 필요하다. 만약 곡면이 매개 변수로 표현된다면, 우리는 $\mathbf{r}_u \times \mathbf{r}_v$로 유도되는 노멀 벡터 $\mathbf{N}$의 방향을 양의 방향으로 설정해서 곡면의 방향을 유일하게 결정한다.
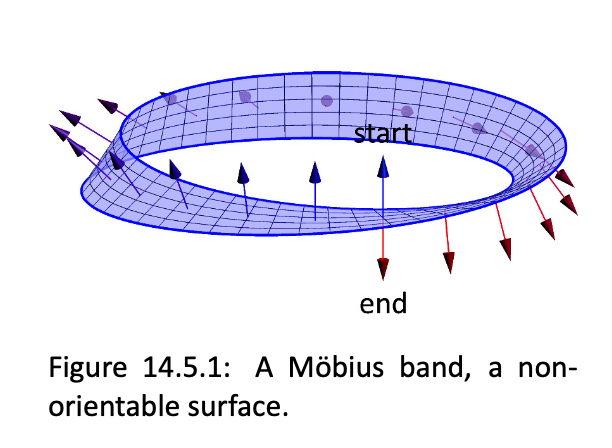
보통의 곡면들은 two-sided surface로 top/bottom side를 결정할 수 있다. 그러나 어떤 곡면들을 two-side로 나뉘지 않는 경우도 있는데, 대표적인 예가 뫼비우스의 띠이다.
이런 경우의 곡면은 무방향(non-orientable) 곡면으로 분류한다.
Gilbert Strang - Calculus Vol 3.
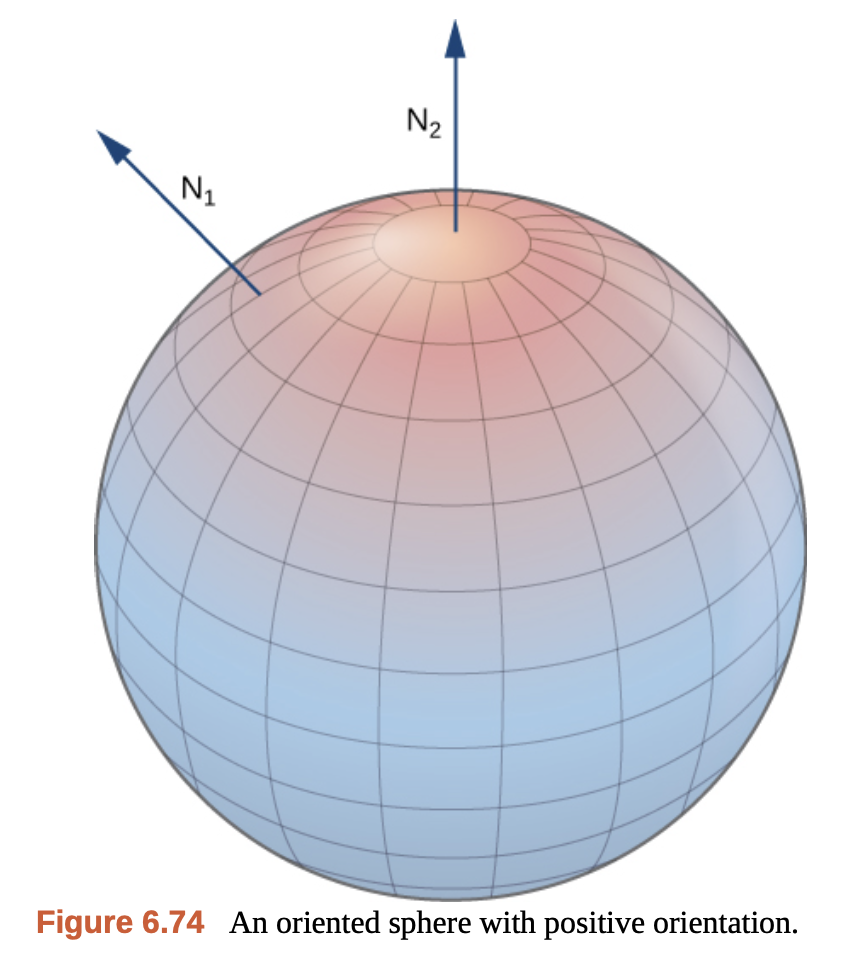
또, 닫힌 곡면의 경우는 곡면의 방향이 항상 바깥(outward) 방향으로 향한다.
$z = f(x, y)$ 꼴
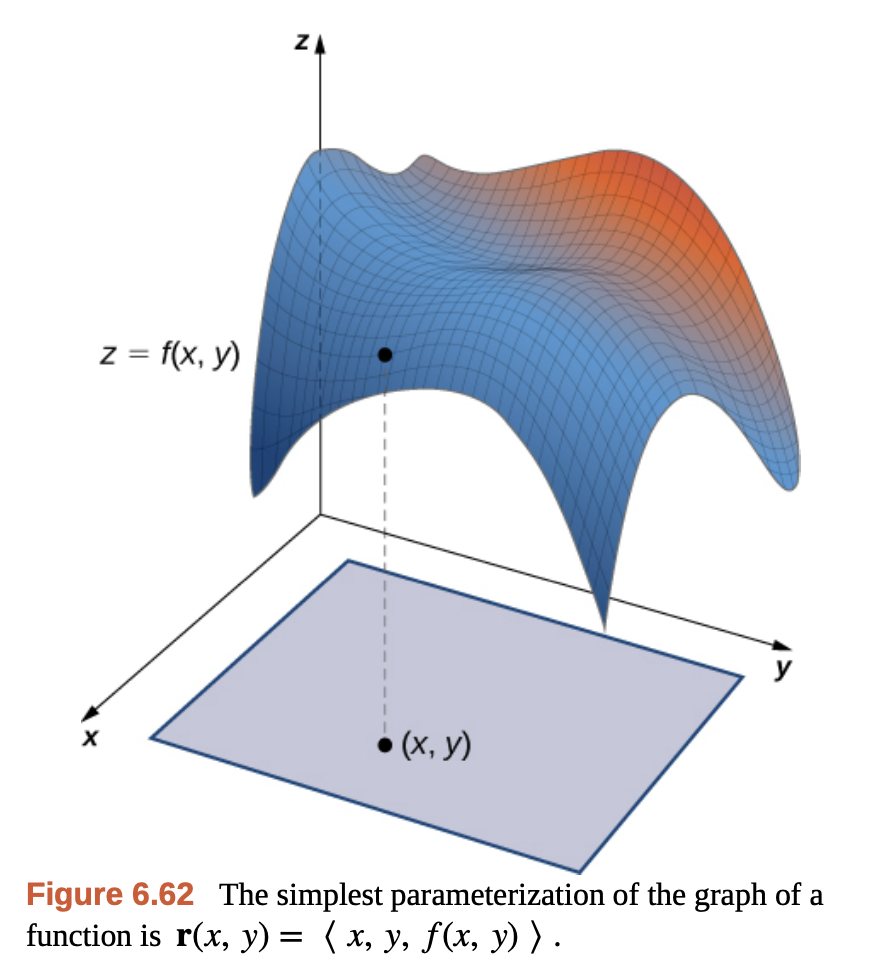
3차원에서 $z = f(x, y)$로 표현되는 매개 곡면들은 $x$, $y$ 변수로 매개화 된 가장 기본적이고 자주 등장하는 매개 곡면의 패턴이다.
Gilbert Strang - Calculus Vol 3.
이 경우에 평면의 넓이에 대한 식은 아래와 같이 적을 수 있다.
\[\begin{aligned} \mathbf{r}_x &= (1, 0, f_x) \\ \mathbf{r}_y &= (0, 1, f_y) \end{aligned}\] \[\mathbf{r}_x \times \mathbf{r}_y = (- f_x, - f_y, 1)\]위의 식에서 알 수 있는 건 $z = f(x, y)$의 꼴에선 곡면이 항상 $+z$ 방향을 top-side로 갖는다.
매개 곡면 위에서의 적분
곡면 적분(Surface Integral)은 선적분의 개념을 확장한 버전이다. 선적분과 마찬가지로 적분은 스칼라장에서의 적분과 벡터장에서의 적분, 두 가지 케이스로 나뉜다.
스칼라장에서
\[\iint_{D} f(x, y, z) \, dS = \iint_{D} f(\mathbf{r}(u, v)) \left| \mathbf{r}_u \times \mathbf{r}_u \right| \, du \, dv\]앞에서 본 곡면 넓이에 대한 적분에서 $f(x, y, z)$가 가중치 형태로 들어간 적분이다. EzEz
벡터장에서
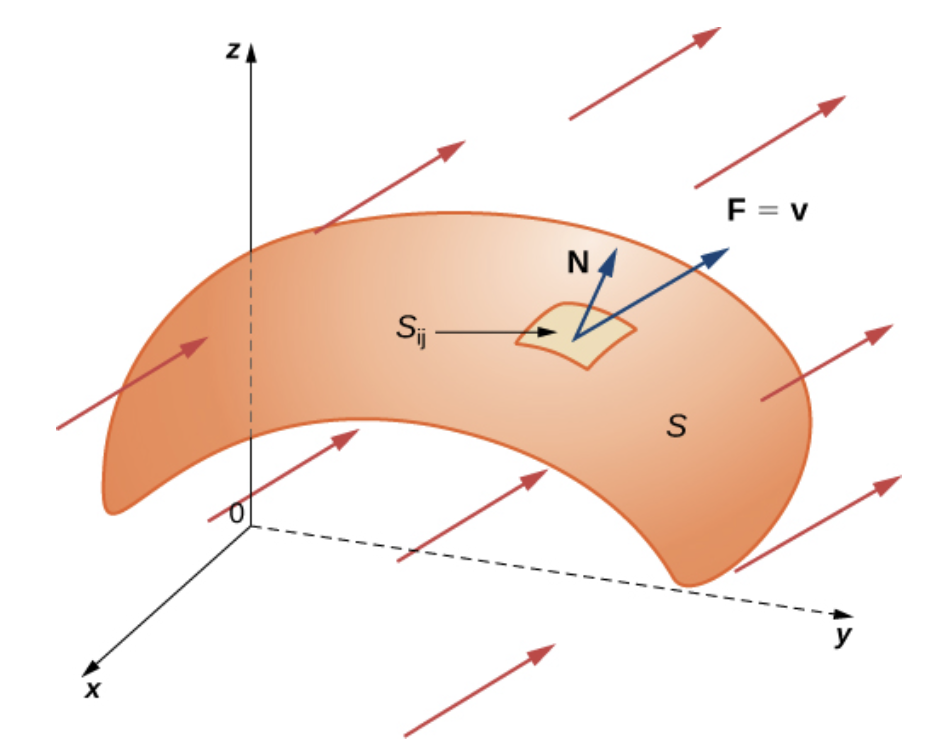Gilbert Strang - Calculus Vol 3.
벡터장에서의 곡면 적분은 그 곡면을 뚫고 나가는 유제들의 흐름을 모은 값과 같다. 적분으로 표현하면 아래와 같다.
어떻게 보면, 벡터장에서의 선적분과 비슷한 식이 만들어졌다. 선적분에서는 아래와 같은 형태였다. (아래식에서는 길이의 미소량 $ds$로 표현된 것이 다르다.)
[그린 정리의 노멀폼]
\[\int_C \mathbf{F} \cdot \mathbf{N} \, ds\]즉, “곡선” $ds$를 뚫고 나가는 유체들의 흐름을 계산했던 걸, “곡면” $dS$로 확장시킨 것.