Divergence Theorem

복수전공하고 있는 수학과의 졸업시험을 위해 학부 수학 과목들을 다시 공부하고 있습니다. 미적분학 포스트 전체 보기

이번 챕터는 Joel Feldman - CLP Calculus 교재의 도움을 많이 받았다.

Divergence Theorem

어떤 물체 $V$에 대한 벡터 장의 발산(div) 값($\nabla \cdot \mathbf{F}$)을 부피 적분하는 것은 부피의 경계 표면 $\partial V$에 대한 벡터장의 면적분을 계산하는 것과 같다는 정리. 수학적으로 표현하면 아래와 같다.

Let $V$ be a bounded solid with a piecewise smooth surface $\partial V$.

Let $\mathbf{F}$ be a vector field that has continuous first partial derivatives at every point of $V$.

Then

\[\iint_{\partial V} \mathbf{F} \cdot \mathbf{n} \, dS = \iiint_{V} \nabla \cdot \mathbf{F} \, dV\]

이때, 주의할 점은 정리가 성립하기 위해선 부피 $V$ 안의 모든 점에서 벡터장 $\mathbf{F}$가 연속이고, 1차 편미분 값을 가져야 한다는 것이다. 이것에 대한 예외가 아래와 같이 원점에서 정의되지 않는 벡터장이다. 물리에서 자주 보이는 녀석.

\[\mathbf{F} = \frac{\mathbf{r}}{\left| \mathbf{r} \right|^3}\]

양(+)전하에 전기장이 대표적인 원점에서 특이점을 갖는 벡터장이다. 중력장은 위의 식에서 방향이 원점을 향하는 벡터장이다.

\[g(\mathbf{r}) = -G \frac{M}{\| \mathbf{r} \|^3} \mathbf{r}\]

with Stokes Theorem

CLP Calculus Textbook

[curl 벡터의 면적분을 부피 적분으로 해석 by 발산 정리]

\[\iint_{\partial V} \nabla \times \mathbf{F} \cdot d\mathbf{S} = \iiint_{V} \nabla \cdot (\nabla \times \mathbf{F}) \, dV = 0\]

직전 포스트인 스토스크 정리에서 “닫힌 곡면에 대한 회전 벡터장의 면적분의 값은 항상 0이 된다”는 것을 살펴보았다. 그렇게 되는 이유를 2가지로 해석할 수 있었는데,

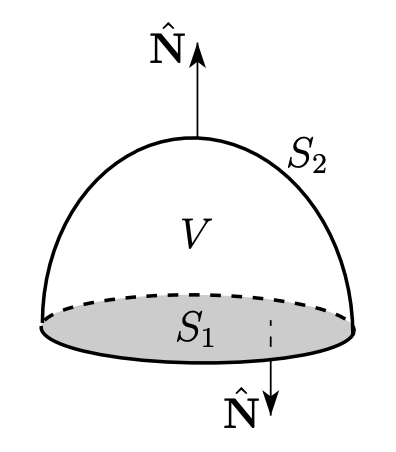
닫힌 곡면을 두 개의 곡면 $S_1$, $S_2$로 분할하고, 스토스크 정리에 의해 두 곡면의 적분을 경계 곡선에 대한 선적분으로 바꾼다. 이때, 두 선적분이 같은 경계 곡선을 서로 반대 방향으로 적분 하므로, 선적분이 서로 상쇄된다. 따라서 적분값은 0.

다른 해석으로는

면적분이 닫힌 곡면이므로, 그것이 어떤 물체 $V$의 경계 곡면이라고 생각해보자. 그러면, 발산 정리에 의해 면적분이 부피 적분으로 바뀌고, 회전 벡터장 $\nabla \times \mathbf{F}$에 발산 연산자를 적용해 발산에 대한 적분으로 바뀐다. 이때, $\nabla \cdot (\nabla \times \mathbf{F}) = 0$이므로 적분값은 0.

An Application of the Divergence Theorem

다른 과목 공부하면서 복습할 때, 내용을 좀 채워보자… 힛…!

the Heat Equation

TDB

Buoyancy

TDB