Logistic Population Model

복수전공하고 있는 수학과의 졸업시험을 위해 학부 수학 과목들을 다시 공부하고 있습니다만… 미분방정식은 졸업시험 대상 과목이 아니라는 걸 나중에 알게 되었습니다… OTL… 그래도 이왕 시작한 거 다시 복습 좀 해봅시다! 🏃 미분방정식 포스트 전체 보기

들어가며

어항에 물고기를 기른다고 생각해보자. 초기에는 암컷-수컷 각각 한 마리만 배치해도, 둘이 새끼를 $N$마리 낳아 물고기 인구 수가 늘어나게 된다. 그리고 그 자손이 또 번식을 해서… 암튼 이렇게 세대를 거쳐서 번식-번식-번식을 하게 되면, 물고기 인구는 상당히 증가하게 될 것이다.

\[2 \rightarrow 2N \rightarrow 2N^2 \rightarrow 2N^3 \rightarrow \cdots\]

요렇게 증가하는 패턴을 지수적 증가라고 하며, 일반해를 적으면 아래와 같다. 일반적인 지수 함수로 표현하기 위해선 밑(base)를 $e$로 대체했다.

\[y(t) = C e^{k t}\]

그러나 현실에선 어항 속 물고기가 무한히 증식하지 않는다. 어항의 공간이 한정 되어 있고, 물고기 수가 많아질수록 먹이 경쟁이 심해지며, 어항 속 환경도 더러워질 것이다. 이런 “자원의 한정” 때문에 인구는 무한히 증가하지 않고 어느 순간부터는 수렴하거나 또는 감소하게 될 것이다.

Logistic Population Model

이런 자원의 한정으로 인한 인구 모형을 모델링 한 것이 바로 “Logistic Population Model”이다.

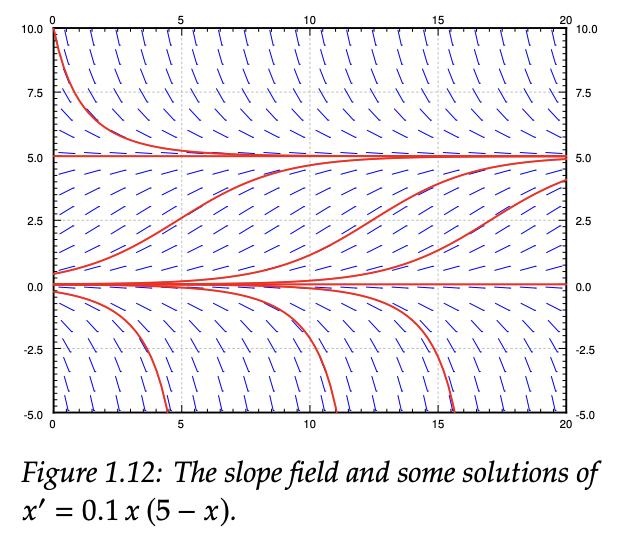Notes on Diffy Qs: Differential Equations for Engineers, Jiří Lebl

보면, 초기에는 지수함수와 같은 증가를 보이지만, 점차 증가폭이 줄어들며, 결국 점근선에 근접하게 된다. 이런 즉, 인구 수에 대한 함수가 이런 S자형 곡선을 그린다는 것을 모델링 한 것이다.

이것을 미분방정식으로 기술하면 아래와 같다.

\[y' = k y(M-y)\]

Solution of ODE

식을 전개하고 아래와 같이 일반화 할 수 있다.

\[y' = Ay - By^2\]

요런 ODE를 풀기 위해선 특별한 치환 테크닉이 필요한데, $u(x) = y(x)^{-1}$로 두고 진행해보면…

\[u' = - \frac{y'}{y^2} = - \frac{Ay - By^2}{y^2} = - A y^{-1} + B = B - Au\]

이제 $u(x)$에 대한 1st-order linear ODE가 되었지만… non-homogeneous linear ODE 이므로, integrating factor도 쓰고… 암튼 한번 풀어보자!!

\[\begin{aligned} u' + Au &= B \\ (Fu)' &= FB \\ \end{aligned}\]

이때, $F(x) = \exp \left(\int A dx \right) = e^{A x}$

이걸 적용하면…

\[\begin{aligned} F(x) \cdot u(x) &= B \cdot \int F(x) dx + C \\ e^{Ax} \cdot u(x) &= B \left(\frac{1}{A} e^{Ax} + C \right) \\ u(x) &= C e^{-Ax} + B/A \end{aligned}\]

이제 치환 했던 $u(x) = 1/y(x)$를 다시 $y(x)$를 기준으로 돌려서 식을 정리하면

\[y(x) = \frac{1}{C e^{-Ax} + B/A}\]

요런 함수가 되고, 요런 꼴의 함수를 “logistic function”라고 부른다. Logistic Population Model의 logistic은 요 함수의 이름에서 유래 했다.

Analysis

위에서는 일반적인 형태의 ODE의 꼴을 살펴보았지만, Logistic Population Model은 아래와 같은 포맷이 더 해석하기 쉽다 ㅎㅎ

\[y' = k y(M-y)\]

Notes on Diffy Qs: Differential Equations for Engineers, Jiří Lebl

ODE에서 각 계수의 의미를 살펴보자.

• $M$은 population이 점근하는 인구 한계값이다.
• $k$는 인구 한계에 얼마나 빠르게 접근하는지에 대한 값이다. $k$값이 클수록 인구 한계에 빠르게 다가간다.

위의 그래프에서 초기 인구가 인구 한계 $M$을 초과한 부분도 흥미롭다. 인구 한계 $M$을 초과 했다면, 그 환경의 인구는 다시 인구 한계로 회귀한다. 💀

Harvesting

어항에서 물고기 인구 수를 조절하기 위해 물고기 중 일부를 수확(?) 한다고 해보자. 수확하는 물고기의 양은 일정할 수도 있고

\[y' = k y(M-y) - h\]

어떤 주기성을 가질 수도 있다.

\[y' = k y(M-y) - h (1 + \sin (2 \pi x))\]

Constant Harvesting

\[y' = k y(M-y) - h\]

수확량이 일정한 경우를 먼저 살펴보자.

위의 ODE 식의 개형을 파악하기 위해 변화량 $y’ = 0$이 되는 지점을 파악해보자.

\[y' = - ky^2 + kM y - h = 0\]

$y$에 대한 2차 방정식이 되고, 근의 공식을 통해 $y$에 대한 해를 유도하면, 실근/중근/허근 3가지 케이스로 나눌 수 있다.

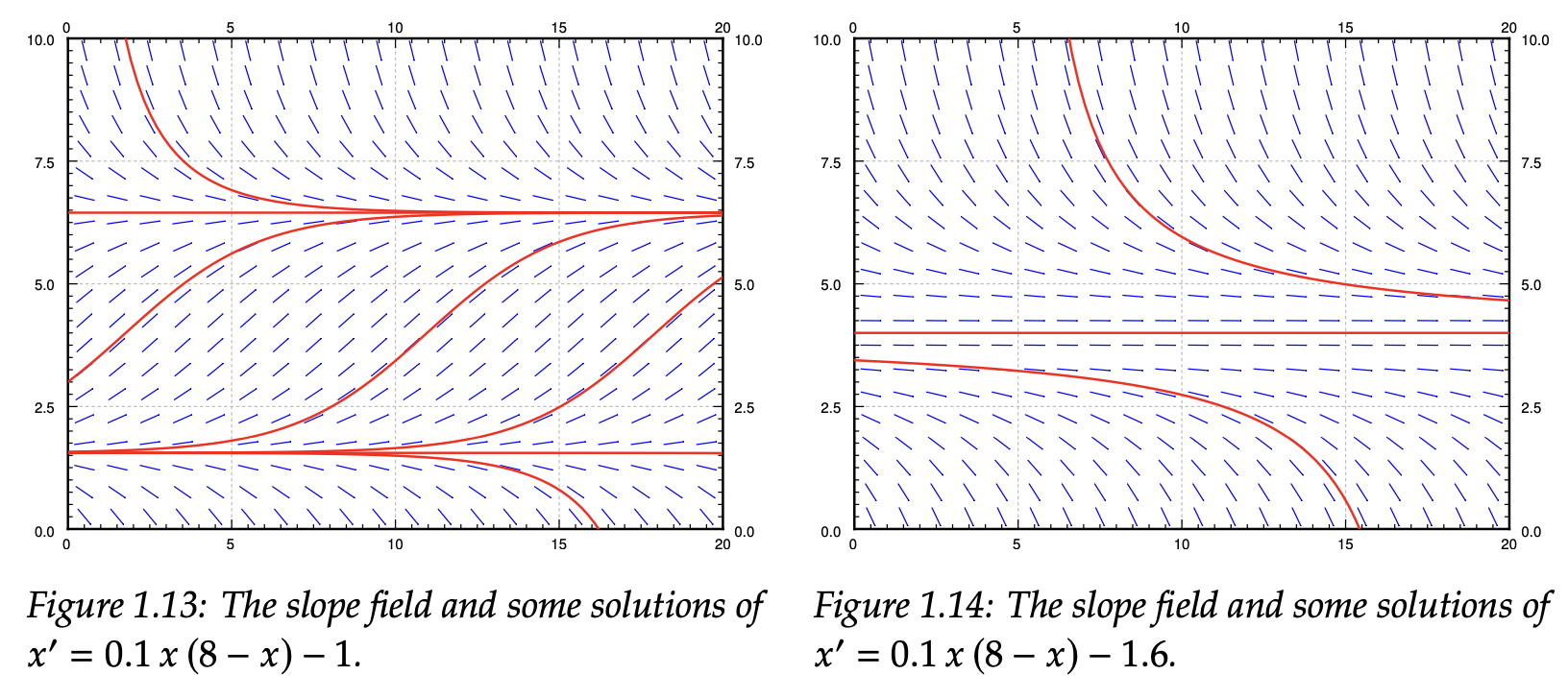Notes on Diffy Qs: Differential Equations for Engineers, Jiří Lebl

• 실근을 갖는 경우
  • ODE가 점근하는 $y$값이 2개 발생한다.
  • 만약 인구의 초기값이 충분히 크지 않다면($y < y_1$), 인구 증가 속도보다 수확 속도가 커서 인구가 소멸한다.
  • 만약 인구의 초기값이 충분히 크다면($y_1 < y < y_2$), 인구 증가 속도가 수확 속도를 이기고 증가하지만, 결국 인구 한계에 부딪힌다.
• 중근을 갖는 경우
  • ODE가 점근하는 $y$값이 하나이다.
  • 수확량이 충분히 커서, 인구 초기값이 충분히 크지 않다면 인구가 수확에 의해 소멸한다.

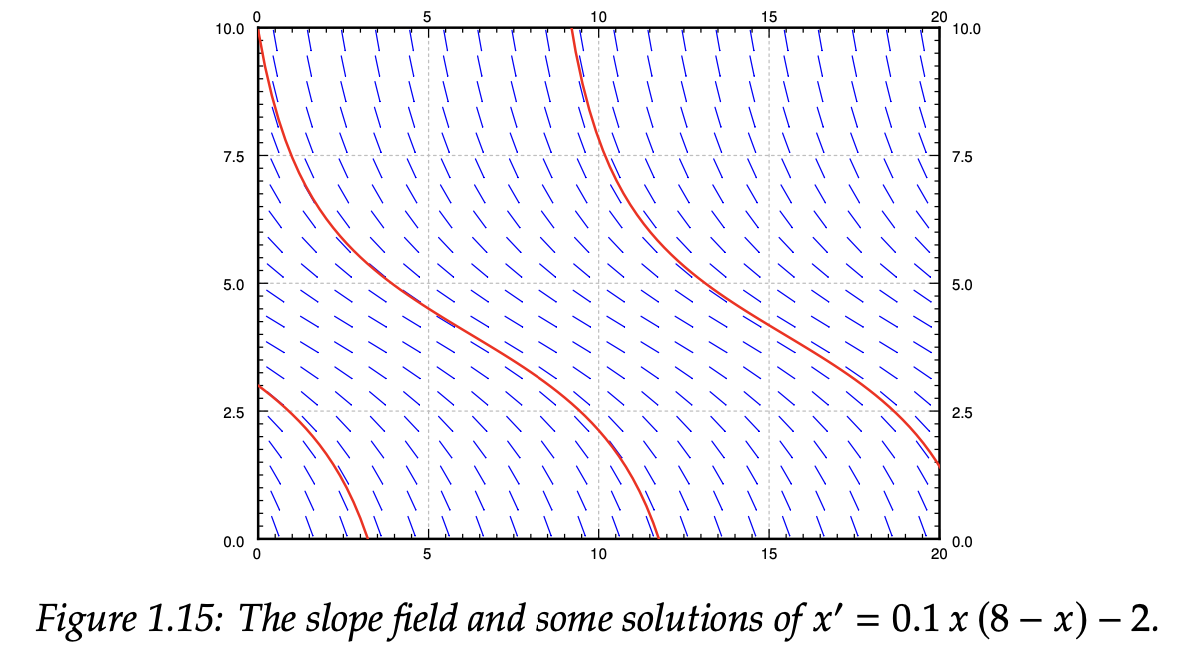Notes on Diffy Qs: Differential Equations for Engineers, Jiří Lebl

• 허근을 갖는 경우
  • 수확량이 인구 증가보다 절대적으로 커서, 어떤 인구로 시작하더라도 인구가 소멸한다. 💀

Periodic Harvesting

\[y' = k y(M-y) - h (1 + \sin (2 \pi x))\]

이번에는 수확이 일정하지 않고, 주기성을 갖는다. 수확량은 $0$부터 $2h$까지 늘었다가 줄었다가 한다.

TDB… 헷갈리는게 있어서 더 공부해보고 추가할 예정… 🙇‍♂️